
- •Практическая работа № 1
- •Часть 1- Решение систем уравнения методом Крамера и методом обратной матрицы
- •Контрольные вопросы
- •Часть 2- Знакомство с алгоритмом «Поиск решения»
- •Целевая функция
- •Построение графика функции
- •Решение
- •Контрольные вопросы
- •Практическая работа № 2 оптимальное использование ресурсов
- •Контрольные вопросы
- •Практическая работа № 3 определение парных коэффициентов корреляции
- •Контрольные вопросы
- •Практическая работа № 4 Моделирование динамики производственных процессов
Контрольные вопросы
В чем заключается смысл метода Крамера?
Что такое определитель системы? С помощью какой функции вычисляется определитель в электронной таблице Excel?
Назовите формулы Крамера.
В чем заключается смысл метода обратной матрицы?
Что такое обратная матрица? С помощью какой функции вычисляется обратная матрица в электронной таблице Excel?
С помощью какой функции вычисляется произведение матриц в электронной таблице Excel? К какой категории относится эта функция?
Задания для самостоятельного выполнения:
1. Методом обратной матрицы решить систему уравнений (вариант задания выбрать по последней цифре номера зачетной книжки):
|
в 5х1+8х2-х3= -7 х1+2х2+3х3= 1 2х1-3х2+2х3= 9
|
в х1+2х2+х3= 4 3х1-5х2+3х3= 1 2х1+7х2-х3= 8
|
|
в 3х1+2х2+х3= 5 2х1+3х2+х3= 1 2х1+х2+3х3= 11
|
в х1+2х2+4х3= 31 5х1+х2+2х3= 29 3х1-х2+х3= 10
|
|
в 4х1-3х2+2х3= 9 2х1+5х2-3х3= 4 5х1+6х2-2х3= 18
|
в 2х1-х2-х3= 4 3х1+4х2-2х3= 11 3х1-2х2+4х3= 11
|
|
в х1+х2+2х3= -1 2х1-х2+2х3= -4 4х1+х2+4х3= -2
|
в 3х1-х2= 5 -2х1+х2+х3= 0 2х1-х2+4х3= 15
|
|
в 3х1-х2+х3= 4 2х1-5х2-3х3= -17 х1+х2-х3= 0
|
в х1+х2+х3= 2 2х1-х2-6х3= -1 3х1-2х2= 8
|
2. Методом Крамера решить систему уравнений (вариант задания выбрать по последней цифре номера зачетной книжки):
|
вар№1
х 3х1-х2-х3-2х4= -4 2х1+3х2-х3-х4= -6 х1+2х2+3х3-х4= -4
|
вар№2
х х1-х2-2х3-3х4= 8 3х1+2х2-х3+2х4= 4 2х1-3х2+2х3+х4= -8
|
|
вар№3
х 2х1+х2+2х3+3х4= 1 3х1+2х2+х3+2х4= 1 4х1+3х2+2х3+х4= -5
|
вар№4
х х1-2х3+3х4= -4 3х1+2х2-5х4= 12 4х1+3х2-5х3= 5
|
|
вар№5
х 3х1+5х2+7х3+х4= 0 5х1+7х2+х3+3х4= 4 7х1+х2+3х3+5х4= 16 |
вар№6
х 3х1+х2-2х3= 9 5х1-7х2+10х4= -9 3х2-5х3= 1
|
|
вар№7
2 х1-3х2-6х4= 9 2х2-х3+2х4= -5 х1+4х2-7х3+6х4= 0 |
вар№8
2 3х1+3х2+3х3+2х4= 6 3х1-х2-х3+2х4= 6 3х1-х2+3х3-х4= 6
|
|
вар№9
х 2х1+х2+х3+х4= 5 х1-х2+2х3+х4= -1 х1+х2-х3+3х4= 10 |
вар№10
4 х1-3х2+4х3= -7 3х2-2х3+4х4= 12 х1+2х2-х3-3х4= 0
|
Часть 2- Знакомство с алгоритмом «Поиск решения»
Цель работы. Получить представление об алгоритме поиска решения Microsoft Excel. Решить задачу определения минимума и максимума функции с использованием этого алгоритма.
Задание
Целевая функция
В качестве примера рассмотрим нахождение экстремумов функции вида: y=(a1+x)(a2+x)(a3+x), графиком которой является кубическая парабола. Если в качестве постоянных a1 , a2 и a3 взять конкретные числа, например, a1 = -1 , a2 = -4 , a3 = 3, то уравнение примет вид: y=(x-1)(x-4)(x+3). Из курса математики известно, что кубическая парабола такого вида имеет два экстремума.
Таким образом, цель решения — найти максимальное (точка максимума) и минимальное (точка минимума) значение данной функции. Поэтому выражение:
y=(x-1)(x -4)(x+3)
назовём целевой функцией, и решение задачи сводится к поиску её экстремумов, путём нахождения переменной x. Можно записать:
y=(x-1)(x-4)(x+3) → MAX и y=(x-1)(x-4)(x+3) → MIN.
Как видно, задача будет иметь два решения: значение x в точке максимума и в точке минимума. Поэтому, вам нужно заготовить две пустые ячейки, где «Поиск решения» разместит в дальнейшем ответы. Рядом разместите ячейки, в которые внесите формулы, соответствующие целевой функции максимума и целевой функции минимума. Примерный результат ваших действий представлен на рисунке.

Так как ячейки, предназначенные для значений x пока остаются пустыми (их числовое значение пока равно нулю), то в ячейках целевых функций будут отображаться одинаковые значения (при x=0 ).

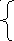 ар№1
ар№1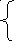 ар№2
ар№2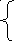 ар№3
ар№3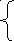 ар№4
ар№4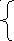 ар№5
ар№5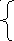 ар№6
ар№6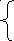 ар№7
ар№7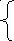 ар№8
ар№8 ар№9
ар№9 ар№10
ар№10 1+х2+2х3+3х4=
1
1+х2+2х3+3х4=
1 1+2х2+3х3-2х4=
6
1+2х2+3х3-2х4=
6 1+2х2+3х3+4х4=
5
1+2х2+3х3+4х4=
5 2-3х3+4х4=
-5
2-3х3+4х4=
-5 1+3х2+5х3+7х4=
12
1+3х2+5х3+7х4=
12 1+5х2+3х3-4х4=
20
1+5х2+3х3-4х4=
20 х1+х2-5х3+х4=
8
х1+х2-5х3+х4=
8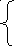 х1-х2+3х3+2х4=
4
х1-х2+3х3+2х4=
4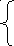 1+2х2-х3+х4=
8
1+2х2-х3+х4=
8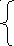 х1+х2-х4=
-9
х1+х2-х4=
-9