Работы по карте / Работа 6 Прямая и обратная задачи

Работа №6.

Прямая и обратная геодезические задачи.

Цель работы: научится решать прямую и обратную геодезические задачи. Проконтролировать между собой работы №2, 4 и 5.

Основная задача геодезии заключается в определении координат точек по результатам полевых измерений.

Прямая задача. Пусть в прямоугольной системе координат дана точка А, которая имеет координаты XA, YA. Требуется определить координаты точки В, если известен дирекционный угол направления АВ - AB и длина линии SAB . Рисунок 6.1.

52

Таким образом, пользуясь приведенными формулами можно по известному дирекционному углу и расстоянию вычислить координаты точки.

Обратная задача заключается в определении дирекционного угла направления и расстояния между точками по известным координатам пунктов.

Пусть имеются точки с координатами: А - XA, YA и В Определим дирекционный угол направления АВ - AB и длину линии SAB . По рисунку имеем:

При решении обратной задачи имеется неопределенность. По формуле вычисляется румб линии r, а не дирекционный угол AB .

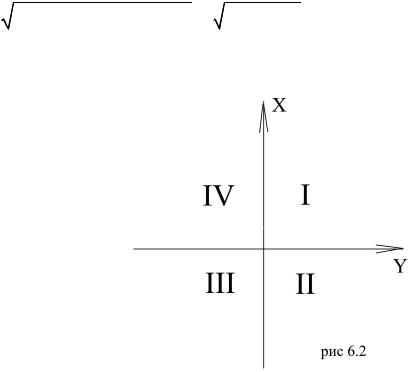
Величина дирекционного угла определяется по формулам связи румбов и дирекционных углов, применение которых зависит от четверти, в которой расположен дирекционный угол. Расположение четвертей показано на рисунке 6.2.

Формулы связи имеют вид:

53

Задание 1.

По измеренным расстояниям и дирекционным углам вычислить координаты точек В и С и сравнить их с измеренными.

Вычисления выполняются в таблице 6.1.

1.В столбец 1 выписываются названия точек. В столбец 2 выписываются измеренные дирекционные углы из работы №5. В столбец 3 выписываются измеренные расстояния между точками из работы №2.

2.В столбцах 4 и 5 вычисляются по формулам (6.3) и (6.4) приращения координат, с округлением до целых метров. В последней строке считаются суммы приращений координат, которые должны быть равны нулю.

3.В строку А, столбцов 6 и 7, выписываются измеренные координаты точки А из работы №4, которые мы примем за исходные.

4.Координаты точек В и С получаются по формулам (6.1) и (6.2):

54

изаписываем в столбцы 6 и 7, в соответствующие строки.

5.В столбцы 8 и 9 выписываются измеренные значения координат точек из работы №4.

6.В 10 и 11 столбце вычисляются расхождения между измеренными и вычисленными значениями координат по формулам:

Величины dX и dY не должны превышать 15 метров. Если условие не выполняется, то это говорит об ошибке в вычислениях или об некачественных измерениях. При этом необходимо проверить вычисления, а потом, если в вычислениях ошибок не будет, заново повторить измерения в работах №№2,4,5.

Таблица 6.1.

Задание 2.

По измеренным координатам вычислить стороны и дирекционные углы.

Вычисления выполняются в таблице 6.2.

55

1.В столбец 1 выписываются названия точек. В столбцы 2 и 3 выписываются измеренные прямоугольные координаты точек А, В, и С из работы №4.

2.В столбцах 4 и 5 вычисляются приращения координат по

формулам:

3.В столбце 6 вычисляются дирекционные углы по формулам (6.5) и

(6.8).

4.В столбец 7 выписываются измененные дирекционные углы из работы №5, и, в столбце 8, вычисляется разность между вычисленными и измеренными дирекционными углами по формуле:

Разность должна быть не более 30’.

5. В столбце 9 вычисляются по формуле (6.7) расстояния между точками. В столбец 10 выписываются из работы №2 измеренные расстояния и, в 11 столбце, вычисляется разность, по формуле:

которая не должна превышать 15 метров.

В случае превышения указанных допусков следует проверить вычисления, а если они верны, то заново провести измерения в работах №№2, 4, 5.

56

Таблица 6.2.

57