
Курс высшей математики
.pdf
|
|
|
|
|
|
|
|
W x |
y1 x y2 x y1 x y2 x 0. |
(2.36) |
|||||
Определение. Выражение W x называется определителем Вронского, или вронскиа- |
|||||||||||||||
ном, решений y1 x и y2 x . |
|
|
|
|
|
|
|
|
|
|
5e2x являются частными |
||||
Пример1. Известно, что функции y e2x, y |
2 |
ex и y |
3 |
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
решениями уравнения y 3y 2y 0. |
|
|
|
|
|
|
|
||||||||
Доказать, что решение y1 и y2 |
образуют фундаментальную систему решений, а y1 |
и y3 |
|||||||||||||
не образуют. |
|
2x |
|
|
x |
|
|
|
2x |
|
|
|
|
|
|
|
2e |
|
e |
, |
|
|
. |
|
|
|
|
|
|||
Решение. y1 |
|
, y2 |
|
y3 5 2e |
|
|
|
|
|
|
|||||
Найдем вронскиан пары решений y1 |
и y2 : |
x y1 x y2 x |
|
|
|||||||||||
|
|
|
|
W1 x y1 x y2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2x ex 2e2x ex e3x 0. |
|
|
|
||||||||
Найдем вронскиан пары решений y1 и y3 |
|
|
|
|
|
|
|||||||||
|
|
W2 x y1 x y3 x y1 x y3 x |
|
|
|
||||||||||
|
|
e2x 10e2x 2e2x 5e2x 10e4x 10e4x 0. |
|
||||||||||||
Вронскиан W1 x 0, следовательно, |
y1 x и |
y2 x образуют фундаментальную пару реше- |
|||||||||||||
ний. |
|
|
|
|
|
|
|
|
y1 x |
и y3 x |
|
|
|
||
Вронскиан W2 x 0, |
следовательно, |
не образуют фундаментальную |
|||||||||||||
пару решений.
Теорема (о структуре общего решения). Если два частных решения y1 x и y2 x линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами образуют фундаментальную систему, то общее решение этого уравнения имеет вид
y C1y1 C2 y2, |
(2.37) |
где C1 и C2 –произвольные постоянные.
Выражение C1y1 C2 y2 называется линейной комбинацией функций y1 x и y2 x .
Доказательство: докажем, что функция (2.37) является решением уравнения (2.35). Для этого подставим в уравнение (2.35) вместо y линейную комбинацию (2.37) и докажем, что оно
превращается в тождество. Так как y1 y2 |
и являются решениями уравнения (2.35), то |
|
|||
Далее имеем |
|
y1 py1 qy1 0 |
и y2 py2 |
qy2 0. |
(2.38) |
|
|
|
|
|
|
|
|
C2 y2 |
|
|
|
C1y1 C2 y2 p C1y1 |
C2 y2 q C1y1 |
|
|
|
|
C1y1 C2 y2 pC1y1 pC2 y2 qC1y1 qC2 y2
C1 y1 py1 qy1 C2 y2 py2 qy2 0.
А это означает, что функция (2.37) является решением уравнения (2.35).
Теперь докажем, что формула (2.37) представляет общее решение уравнения (2.35). Для этого надо показать, что любое решение уравнения (2.35) можно получить из формулы (2.37) при некоторых значениях постоянных C1 и C2. Пусть y x – какое-либо частное решение уравнения (2.35). Пусть, далее, x0 некоторое число из области определения решения y x ;
обозначим x0 y0 , x0 y0. Отсюда следует, что решение y x удовлетворяет на-
чальным условиям с начальными данными x0, y0, y0 . Осталось показать, что решение
81
y x может быть получено из формулы (2.37) при надлежащих значениях C1 C10 и
C2 C20 . Для этого рассмотрим систему алгебраических уравнений
y C y x C |
2 |
y x , |
(2.39) |
|||
|
0 |
1 |
1 |
2 |
||
y0 C1y1 x C2y2 x , |
|
|||||
где y1 x и y2 x – решение из данной фундаментальной системы решений, x0, y0, y0 по-
лученные выше начальные данные;C1 и C2 –неизвестные, которые предстоит определить. Ум-
ножая первое уравнение из (2.39) на y2 x0 , второе – на y2 x0 и вычитая второе уравнение из первого, получим
y1 x0 y2 x0 y2 x0 y2 x0 C1
y0 y2 x0 y0 y2 x0 ,
|
|
y2 |
(x0), |
|
|
|
|
||||
или W(x0) c1 y0 y2 |
(x0) y0 |
|
|
|
|
||||||
откуда ввиду того, что W x0 0, найдем |
y0 y2 x0 y0 y2 x0 |
|
|
||||||||
|
C C |
|
|
|
. |
||||||
|
|
|
|
|
|||||||
|
1 |
10 |
|
|
|
|
W x0 |
|
|
|
|
Аналогично получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 x0 |
|
||
|
|
|
|
|
|
|
|
||||
|
C2 C20 |
y0 y2 |
x0 y0 |
. |
|||||||
|
|
W x0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим сейчас частное решение, которое получается из (2.37), если взять C1 C10 и C2 C20 : y x C10 y1 x C20 y2 x . Ввиду (2.39) составленное решение y x удовлетво-
ряет начальным условиям с начальными данными x0, y0, y0 , т.е. |
y x0 x0 , |
y x0 x0 . |
|
Следовательно, согласно теореме Коши о единственности решения, удовлетворяющего данным начальным условиям, имеем
x y x C10 y1 C20 y2. |
(2.40) |
Найдем решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Для нахождения общего решения уравнения (2.35) достаточно найти два его частных решения, образующих фундаментальную систему.
Будем искать эти частные решения уравнений (2.35) в виде
|
|
|
|
y ekx, |
(2.41) |
где k=const; |
|
|
|
|
|
тогда y kekx , y k2 ekx . |
|
|
|
|
|
Подставим выражение для y, y |
и y в уравнение(2.35), получим |
|
|||
k2ekx pkekx qekx |
0, т.е. |
ekx k2 |
pk q 0. |
|
|
Так как ekx 0, то |
|
|
|
|
|
|
|
|
k2 |
pk q 0. |
(2.42) |
Определение. Уравнение (2.42) называется характеристическим уравнением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Для составления характеристического уравнения (2.42) достаточно в уравнении (2.35)
заменить y , y и y соответственно на k2, k и 1.
82

Решив характеристическое уравнение по формуле: k1,2 |
|
p p2 |
4q |
|||
|
|
|
|
, найдем его |
||
|
|
2 |
|
|||
|
|
|
|
|
|
|
корни k1 и k2 , а следовательно, и частные решения уравнения (2.35): |
|
|
||||
y ek1x |
, y |
2 |
ek2x. |
(2.43) |
||
1 |
|
|
|
|
|
|
При решении характеристического уравнения возможны три случая.
Случай 1. Корни характеристического уравнения действительны и различны .
В этом случае имеем два частных решения уравнения (2.35): y1 ek1x и y2 ek2x.
Покажем, что эти решения образуют фундаментальную систему решений. Для этого рассмотрим вронскиан:
W x y1 x y2 x y1 x y2 x ek1xk2ek2x
k1ek1xek2x k2e k1 k2 x k1e k1 k2 x e k1 k2 x k2 k1 0,
т.е. e k1 k2 x 0 и k2 k1.
Следовательно, в этом случае решение общего уравнения (2.35) имеет вид
y C ek1x |
C |
2 |
ek2x. |
(2.44) |
1 |
|
|
|
Случай 2. Корни характеристического уравнения действительны и равны: k1 k2 k .
В этом случае непосредственно находим лишь одно частное решение: y2 xekx .
Вторым частным решением является решение y2 xekx .Действительно,
|
|
kx |
kx |
xe |
kx |
|
e |
kx |
|
|
kx |
e |
kx |
1 kx , |
|
|
|
|
|
|
|
|
|
|||||||||||
y2 |
xe |
|
xe |
|
|
|
|
xke |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y2 |
e |
kx |
|
|
|
|
|
kx |
|
|
|
|
ke |
kx |
1 kx e |
kx |
k |
|
|
|
|
|
|
|
|
|
||||||||
|
1 kx e |
|
|
1 kx |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
ekx 2k k2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
y и |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Подставим выражение для y, |
в уравнение (2.35), получим |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ekx 2k k2x pekx 1 kx qxekx |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ekx x k2 pk q 2k p 0. |
|
|
|
|
|
||||||||||||||||
|
Так как k |
является корнем характеристического уравнения k2 pk q 0, корни квад- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ратного трехчлена находятся по формуле |
k |
|
p p |
2 4q |
. |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Если k k |
2 |
k , то p2 |
4q 0, т.е. k |
p |
или |
|
2k p 0. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ekx и y |
|
xekx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Покажем, что y |
2 |
образуют фундаментальную систему решений. Для |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этого рассмотрим вронскиан: |
|
|
|
|
|
|
|
|
|
|
|
|
|
kx |
|
kx |
1 kx |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
W x y1 x y2 x y1 x y2 x e |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e2kx 1 kx kx e2kx 0. |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Таким образом, в этом случае общее решение уравнения (2.35) имеет вид |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ekx C |
C |
2 |
x . |
(2.45) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Случай 3. Корни характеристического уравнения комплексные:
83

k |
p |
p2 4q |
, |
p2 4q 0. |
|
|
|
|||||||
|
|
|
|
|
||||||||||
1,2 |
|
2 |
i2 4q p2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Тогда k |
p |
|
p |
|
i |
4q p2 |
|
. |
||||||
|
|
|
|
|
|
|
||||||||
1,2 |
|
2 |
2 |
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
p |
|
|
|
4q p2 |
|
|
|
|
||||
22 1 a bi и k2 a bi b 0 .
Вэтом случае y1 eax cosbx и y2 eax sin bx являются решениями уравнения (2.35) и,
вычисляя вронскиан, убедимся, что они составляют фундаментальную систему. Действительно,
y1 |
e |
ax |
|
cosbx e |
ax |
|
|
ax |
cosbx |
|||
|
|
|
|
cosbx a e |
|
|
||||||
eax sin bx b eax |
a cosbx b sin bx . |
|||||||||||
|
e |
ax |
|
sinbx e |
ax |
|
|
ax |
sinbx |
|||
y2 |
|
|
|
|
sinbx a e |
|
|
|||||
eax cosbx b eax a sinbx b cosbx .
Подставим выражения для y1 x , y1 x , y2 x и y2 x в вронскиан (2.36), получим:
W x y1y2 y1y2 eax cosbx eax asinbx bcosbx
eax acosbx bsinbx eax sinbx e2ax cosbx asinbx bcosbx
e2ax sinbx acosbx bsinbx e2ax acosbxsinbx bcos2bx
asinbxcosbx bsin2bx e2axb cos2bx sin2bx e2axb 0.
При вычислении воспользовались основным тригонометрическим тождеством: cos2 sin2 1.
Таким образом, общее решение уравнения (2.35) в случае комплексных корней характеристического уравнения имеет вид
|
|
|
y C eax cosbx C |
2 |
eax sin bx, или |
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y eax C cosbx C |
sinbx . |
|
(2.46) |
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
||
Рассмотрим примеры решения дифференциальных уравнений с постоянными коэффи- |
||||||||||||||||||
циентами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти частное решение уравнения y 7y 12y 0 удовлетворяющее на- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чальным условиям y 0 1, y 0 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Составим характеристическое уравнение, заменив y , y , y на k2, |
k , 1 соот- |
|||||||||||||||||
ветственно, получим k2 7k 12 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
7 |
|
72 |
4 12 |
|
7 |
|
|
|
|
7 1 |
, откуда k |
|
|
||||
Корни найдем по формуле k |
|
1 |
1 |
3 и |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1,2 |
|
2 |
|
2 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k2 4. Подставляя найденные значения k1 |
и k2 |
в формулу (2.44), получим общее решение |
||||||||||||||||
y C e 3x |
C |
2 |
e 4x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя общее решение, получим
y C1e 3x 3 C2e 4x 4 3C1e 3x 4C2e 4x .
Согласно заданным начальным условиям имеем
84
|
|
30 |
C2e |
4 0 |
|
|
|
|
|
|
1 C1 C2 |
|
|||||||||||||
1 C1e |
|
|
|
|
|
|
|
|
, или |
, |
|||||||||||||||
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
|
|
||||||||
2 3C e |
4C |
2 |
e |
4 0 |
|
|
2 3C1 4C2 |
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 1 C1 |
|
|
|
|
|
|
C2 1 C1 |
|
|
||||||||||||||||
или 2 3C 41 C |
, или 2 C |
|
|
, откуда |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|||||
C1 2 и C2 |
1. Таким образом, искомым частным решением является функция |
||||||||||||||||||||||||
y 2e 3x e 4x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи для контрольных заданий |
|||||||
|
Найти решение уравнений |
|
|
|
|
|
|||||||||||||||||||
6.01 а) |
y |
|
5y |
|
6y 0, если |
y 0 |
1, |
|
|
|
|
||||||||||||||
|
|
|
|
|
y 0 2; |
|
|||||||||||||||||||
б) |
|
y 16y 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в) y 6y 9y 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
6.02 а) |
y |
2y |
0, если |
y 0 |
, |
|
|
|
|
||||||||||||||||
|
|
|
|
y 0 1; |
|
|
|||||||||||||||||||
б) y 8y 16y 0; |
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
в) y 6y 25y 0. |
y 0 1 |
|
|
|
|||||||||||||||||||||
6.03 а) |
y |
|
8y |
|
15y 0, если |
|
|
|
|||||||||||||||||
|
|
|
|
, y 0 0; |
|
||||||||||||||||||||
б) |
|
y |
|
2y |
|
5y 0, если |
y 0 |
y |
|
|
|
||||||||||||||
|
|
|
|
0 1; |
|
||||||||||||||||||||
в) y 10y 25y 0. |
|
|
|
|
|
|
|
|
|||||||||||||||||
6.04 а) |
y 3y 0; |
|
|
|
y 0 1, |
|
|
|
|
|
|
||||||||||||||
б) |
|
y |
|
9y 0, если |
|
|
|
|
|
|
|||||||||||||||
|
|
y 0 6; |
|
|
|||||||||||||||||||||
в) y 12y 36y 0. |
|
|
|
|
|
|
|
|
|||||||||||||||||
6.05 а) |
y 14y 49y 0; |
|
|
|
|
|
|
|
|
||||||||||||||||
б) |
|
y |
|
4y |
|
0, если |
y 0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
y 0 1; |
|
|
||||||||||||||||||||
в) y 4y 4y 0.
6.06а) y 4y 0;
б) y 2y 8y 0;
в) |
y |
|
8y |
|
16y 0 |
|
|
|
|
, если y 0 y 0 1. |
|||||
6.07 а) |
y |
|
3y |
|
2y 0, |
если y 0 1, |
|
|
|
y 0 1; |
|||||
б) |
y |
|
8y |
|
16y 0 |
|
|
|
|
, если y 0 y 0 1; |
|||||
в) |
y 16y 0. |
|
|
||||
6.08а) y 2y 5 0, если y 0 y 0 1; б) y 2y 0;
в) y 14y 49y 0.
6.09 а) |
y |
|
y 0, если y 0 2 |
|
|
||
|
, y 0 1; |
||||||
б) |
y 64y 0; |
|
|
||||
в) |
y 20y 100y 0. |
y 0 2, |
|
||||
6.10 а) |
y |
|
8y |
|
20y 0, если |
|
|
|
|
y 0 8; |
|||||
б) y 7y 12y 0; |
|
|
|||||
в) y 2y y 0. |
|
|
|||||
6.11 а) |
y 3y 4y 0; |
|
|
||||
85

б) y 2y 5y 0, если y 0 y 0 1;
в) y y 1 y 0. 4
6.12а) y 9y 14y 0; б) y y 0;
в) y 10y 25y 0, если y 0 2, y 0 8.
6.13 а) |
y |
|
3y |
|
2y 0, если |
y 0 1, |
|
|
|
y 0 3; |
|||||
б) |
y 9y 0; |
|
|
||||
в) |
y 22y 121y 0. |
|
|
||||
6.14а) y y 0;
б) y 6y 45y 0;
в) y 6y 9y 0, если y 0 2, y 0 1.
6.15 |
а) |
y |
|
2y |
|
2y 0, если |
y 0 |
|
|
|
|
||||||||
|
|
|
1, y 0 3; |
||||||||||||||||
|
б) y 2y 0; |
|
|
|
|
|
|
|
|
|
|||||||||
|
в) y 2y y 0. |
|
|
|
|
|
|
|
|
|
|||||||||
6.16 |
а) |
y |
|
6y |
|
8y 0, если |
|
|
|
|
|||||||||
|
|
|
y 0 y 0 1; |
||||||||||||||||
|
б) |
y 16y 0; |
|
|
|
|
|
|
|
|
|
||||||||
|
в) y y |
1 |
y 0. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
6.17 |
а) |
y 4y 8y 0; |
y 0 2, |
|
|
|
|
||||||||||||
|
б) |
y |
|
9y 0, если |
|
|
|||||||||||||
|
|
y |
0 6; |
||||||||||||||||
|
в) 9y 6y 1 0. |
|
|
y 0 3 |
|
|
0 0; |
||||||||||||
6.18 |
а) |
y |
|
y |
|
2y 0, если |
|
|
|||||||||||
|
|
|
, y |
||||||||||||||||
|
б) 16y 8y y 0; |
|
|
|
|
|
|
|
|
|
|||||||||
|
в) |
y 25y 0. |
|
|
|
|
|
|
|
|
|
||||||||
6.19 |
а) |
y |
|
8y |
|
7 0, если |
|
|
|
|
|
|
|||||||
|
|
|
y 0 y 0 1; |
||||||||||||||||
|
б) |
y 16y 0; |
|
|
|
|
|
|
|
|
|
||||||||
|
в) 25y 10y y 0. |
|
|
|
|
|
|
|
|||||||||||
6.20 |
а) |
y |
|
5y |
|
4y 0 |
, если y 0 |
|
|
||||||||||
|
|
|
y |
0 1; |
|||||||||||||||
|
б)49y 14y y 0; |
|
|
|
|
|
|
|
|||||||||||
|
в) |
y 121y 0. |
|
|
|
|
|
|
|
|
|
||||||||
6.21 |
а) |
y 2y y 0; |
|
|
|
|
|
|
|
|
|
||||||||
|
б) |
y |
6y 9y 0, если |
y 0 |
|
|
|
||||||||||||
|
y 0 1; |
||||||||||||||||||
|
в) y 2y 2y 0. |
|
|
|
|
|
|
|
|
|
|||||||||
6.22 |
а) 2y 3y 5y 0; |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y |
4y 0, если |
|
|
|
|
|
|
|
|
|
|||||||
|
б) |
y |
|
|
1, |
|
|
2; |
|||||||||||
|
|
|
|
y |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
||||||
в) 64y 16y y 0.
6.23а) y 6y 5y 0, если y 0 y 0 1; б) y 81y 0;
в) 4y 4y y 0.
86
6.24а) y 8y 7y 0, если y 0 y 0 1; б) y 4y 0;
в) 16y 8y y 0.
6.25 а) y y 0, если y 0 y 0 1;
б) y 16y 0;
в) y 26y 169y 0.
Вопросы для самопроверки
1.Что называется дифференциальным уравнением первого порядка?
2.Что называется общим решением дифференциального уравнения первого порядка, интегральными кривыми?
3.Дайте геометрическую иллюстрацию частного и общего решений дифференциального уравнения первого порядка.
4.Сформулируйте задачу Коши.
5.Дайте определение дифференциального уравнения с разделяющимися переменными и укажите метод его интегрирования.
6.Сформулируйте теорему существования и единственности решения дифференциального уравнения с разделяющимися переменными.
7.Дайте определение однородного дифференциального уравнения и способа его решения.
8.Что называется линейным дифференциальным уравнением первого порядка? Дайте способ его решения.
9.Сформулируйте теорему Коши для линейного дифференциального уравнения.
10.Что называется линейным дифференциальным уравнением второго порядка?
11.Сформулируйте задачу Коши для линейного дифференциального уравнения второго порядка.
12.Дайте определение фундаментальной системы решений и определителя Вронского.
13.Докажите теорему о структуре общего решения.
14.Дайте определение характеристического уравнения.
15.Структура решения линейного однородного дифференциального уравнения.
Контрольная работа №4
Глава 3.Кратные интегралы
§1. Двойной интеграл
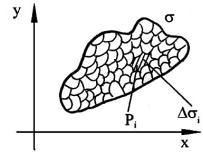
Рассмотрим задачу о нахождении массы материальной двумерной пластинки , если известна плотность (x;y) в каждой ее точке. Разделим данную область произвольным образом на nчастей (рис.29) P(x;y). В каждой элементарной части
i |
выберем по одной точке i i;ni и вычислим плотность |
|
87 |
Рис.29
i;ni в точке i. Тогда масса элементарной пластинки части i приближенно будет равна
i;ni i .
Для массы всей пластинки получаем
m i;ni i . |
(3.1) |
i |
|
Приближение (3.1) будет тем точнее, чем мельче будет разбиение области на элементарные части, т.е. чем меньше будет наибольшее расстояние между произвольными точками любой элементарной области i . Следовательно, можно принять, что
m |
lim i;ni i , |
(3.2) |
|
|
0 i |
|
i- это наибольшее |
где наибольший из диаметров элементарных частей |
i (диаметр |
||
расстояние между произвольными ее точками).
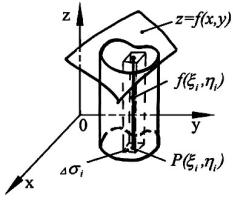
К аналогичному выражению приходим при рассматривании задачи вычисления объемов цилиндрических тел.
Пусть требуется вычислить объем тела, ограниченного сверху непрерывной поверхностью z f x; y f x;y 0 , снизу – конечной замкнутой областью плоскости 0xy и с бо-
ков – цилиндрической поверхностью, построенной на границе области |
и имеющей обра- |
||
зующие, параллельные оси 0z (рис.30). |
|
i |
|
Делим область на элементарные области |
i. В каждой |
выбираем по одной |
|
|
точке |
i i;ni . Тогда объем |
|
|
прямого элементарного цилин- |
|
|
дра, ограниченного сверху по- |
|
|
верхностно |
z f x; y и снизу |
|
областью – областью i, при- |
|
|
ближенно |
равен f ( i; i) i , |
|
где i - |
площадь соответст- |
|
вующей элементарной области. |
|
|
Для объема всего нашего ци- |
|
|
линдрического тела получаем |
|
|
приближение |
|
|
V f i;ni i . |
(3.3) |
|
i |
|
Приближение (3.3) будет тем точнее, чем меньше будет наибольший из диаметров |
||
элементарных областей i . Следовательно, можно и в этом случае принять, что |
||
V |
lim f i;ni i . |
(3.4) |
|
0 i |
|
Необходимость рассмотрения выражений вида (3.1), (3.3) и пределов (3.2), (3.4) возникает при решении многих других физических и геометрических задач. В связи с этим дается следующее определение. Пусть функция f x; y определена в некоторой области . Делим об-
ласть на n элементарных частей i. В каждой части i выбираем по одной точке
i i;ni и составляем выражение
Sn f i;ni i . |
(3.5) |
i |
|
Определение 1. Выражение вида (3.5) называется интегральной суммой для функции f x; y в области .
88
Обозначим через наибольший из диаметров элементарных областей i при разбие-
нии области . |
|
|
|
|
Определение 2. Если существует предел |
f i;ni i , |
|
||
|
S lim |
(3.6) |
||
|
0 |
i |
и выбора точек i i;ni , то |
|
который не зависит от способа деления области на части i |
||||
этот предел называется двойным интегралом от функции f x; y |
по области и обозначается |
|||
f x; y d , или f x;y dxdy. Здесь |
f x; y называется подынтегральной |
функцией; - |
||
областью интегрирования; x и y переменными интегрирования; d (или dxdy) – элементом площади.
Таким образом, по определению
f x; y dxdy lim f i;ni i . |
(3.7) |
|
|
0 i |
|
Функция f x; y называется интегрируемой в области . Всякая непрерывная в ограни-
ченной замкнутой области функции f x;y интегрируется в ней. В дальнейшем мы огра-
ничимся рассмотрением только непрерывных функций.
Двойной интеграл обладает следующими простейшими свойствами:
если f x; y C f1 x; y , то f x;y dxdy C f x;y dxdy ;
если f x;y f1 x;y f2 x;y , то f x;y dxdy
f1 x;y dxdy f2 x;y dxdy ; если область состоит из двух областей 1 и 2 (рис.31), то
f x; y dxdy
f1 x;y dxdy f2 x;y dxdy .
1 |
2 |
|
|
|
|
|
|
|
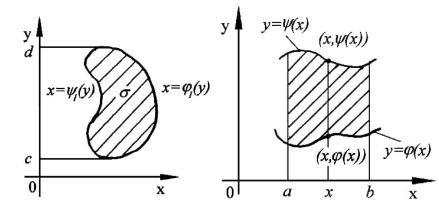
Область на плоскости x0y назовем простой областью: |
y x , снизу y x |
|||||||
1) (относительно оси 0x) если она ограничена сверху линией |
||||||||
(функции (x) |
и x непрерывны) и с боков отрезками прямых x a и x b (рис32); в част- |
|||||||
ных случаях один из этих отрезков (или оба вместе) могут превратиться в точку (рис.33); |
|
|
||||||
2) (относительно оси 0y ) если она ограничена слева линией x 1 y , справа x 1 y |
||||||||
(функции 1 y |
и 1 y непрерывны) и сверху и снизу отрезками прямых |
y d |
и |
y c |
||||
(рис.34, 35). |
|
|
|
|
|
|
|
|
Теперь перейдем к непосредственному вычислению двойного интеграла. Для этого сно- |
||||||||
ва рассмотрим задачу о нахождении массы материальной двумерной пластинки . |
|
|
|
|||||
|
|
Пусть |
материальная |
|||||
|
область |
|
ограничена снизу |
|||||
|
кривой |
y x , |
сверху |
– |
||||
|
кривой |
y x , с |
боков |
– |
||||
|
прямыми |
x a |
и |
x b |
||||
|
(рис.36), т.е. является простой |
|||||||
|
областью вида 1 относитель- |
|||||||
|
но |
оси |
0x. |
Пусть, |
далее, |
|||
Рис.35 |
Рис.36 |
функция f x;y выражает плотность (т.е. “концентрацию массы”) |
в точке x; y . Для некото- |
|
рого x значения выделим материальный отрезок от точки x; x |
до точки x; x и вычис- |
|
лим массу m x ,сконцентрированную на этом отрезке, по формуле |
|
|
|
x |
|
m x |
f x;y dy |
|
|
x |
|
Далее, спроектируем нашу материальную пластинку на ось 0x, получим материальный отрезок a;b , плотность которого в каждой точке x будет выражаться функцией m x . Следовательно, масса этого отрезка и всей области будет
b |
b x |
|
|
b |
x |
|
|
x;y dy |
|
|
|
m m x dx f |
dx dx f x;y dy . (3.8) |
||||
a |
a x |
|
|
a |
x |
С другой стороны , выше было доказано:
m lim |
f i;ni i f x; y dxdy . |
|
0 |
i |
|
Таким образом, для вычисления двойного интеграла от функции f x; y по области получим следующую формулу, сводящую ее вычисление к повторному интегралу:
|
b x |
|
b x |
|
|
||
f x;y dxdy |
f x;y dy dx dx f x;y dy. |
(3.9) |
|||||
|
|
x |
|
a x |
|
|
|
a |
|
|
|
||||
|
|
|
|
Заметим, что в случае |
|||
|
|
|
вычисления |
объема |
цилинд- |
||
|
|
|
рических |
тел |
интеграл |
||
|
|
|
x |
|
|
|
|
|
|
|
|
f x; y dy |
дает |
площадь |
|
|
|
|
x |
|
|
|
|
|
|
|
S x поперечного сечения |
||||
|
|
|
нашего тела (рис.37), следова- |
||||
|
|
|
тельно, весь объем V будет |
||||
Рис.37 |
|
|
|
|
|
|
|
b |
b x |
|
b x |
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
V S x dx |
f x;y dy dx dx f x;y dy. |
|
|||||
a |
a x |
|
a x |
|
|
|
|
Если же область есть простая область вида 2, то всякая прямая, параллельная оси 0x |
|||||||
и проходящая внутри отрезка |
|
|
|
|
|
|
|
a;b , пересекает границу в двух точках: 1 y ;y |
и 1 y ;y |
(рис.38). Двойной интеграл по |
|||||
такой области вычисляется по формуле |
|
|
|
|
|
1 y |
|
|
|
|
|
|
d |
||
|
|
|
f x; y dxdy dy |
|
f x; y dx |
||
|
|
|
|
|
c |
1 y |
|
|
|
|
|
. |
|
|
(3.11) |
|
|
|
|
Наиболее простой вид |
|||
|
|
|
формулы (9.3) и (11.3) при- |
||||
|
|
|
нимают в случае прямоуголь- |
||||
Рис.38 Рис.39
