Курс высшей математики

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

б) Вычислить длину дуги кривой y lnsin xот

б) Вычислить длину дуги кривой y lnsin xот

.pdf

Скачиваний:

Добавлен:

10.03.2016

Размер:

6.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 184 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

lim

1 f x

a 1 f x

b x

1 f x

n 1

а так как очевидно, что наибольшее звено

ломаной и длина

наибольшего из отрезков

a1;x1 , x1;x2 ,

, xn 1;b

(на которые разбился отрезок a;b ) стремятся к нулю одновре-

менно, то

1 f c1

x1 a 1 f c2

lim

1 f cn

b xn 1

b
	1 f		2
				dx,т.к. в квадратных скобках стоит интегральная сумма для написанного инте-
		x

грала.

Пример 3. Найдем длину линии y 2 x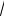x , 0 x 3. 3

																															2				3									2		3				3	1								1

				Решение.																															2															2									2
				Решение.										Так как									y								3			x									3			2		x								x				, то по формуле (1.20) получаем				ли-

нии:																																														1
3															3							1																									1 3


			1					x		2 dx 1 x																d 1 x													1 x 2											\|
																								2															1 x 2
																								2
0															0																												1		1					0
0							3								0																												2		1					0
																																											2
	2	1 x				3						2	1 3						3			1 0											3					2			8 1									14				.
	2											2							2																			2												14

3			2 \|						3																								2			3														3
			0
			0
																																																												dx dx.
				Здесь воспользовались тем, что d 1 x 1 x																																																								dx dx.
				Пример 4. Найти длину дуги кривой y																																																1			x2					1		ln x	от x 1 до x e.
				Пример 4. Найти длину дуги кривой y																																																			x2					2		ln x	от x 1 до x e.
																																																		4										2
				Решение. Воспользовались формулой (1.20). Найдем y :
			1		x2				1								1			2x2 1														1	1							1					1
y											ln x																																	x						x.
y			4						2		ln x						4																	2								2		x			2			x.
			4						2								4																	2	x							2					2
																2									1										1							2							1							2					1		1


																			1											x														1													2x
											1 y								1											x														1					4		x						2x						x2
				Откуда																							2								x														4													x	x2
															1		x		2			1						1												1			x		2				1	1
												1																																														.
												1										2								4x2										4									2				4x2					.
															4							2								4x2										4									2				4x2
				Следовательно,
							e																				e	1								1
							e											2									e	1								1
										1 y					x						dx											x								dx
										1 y					x						dx											x								dx
			1																								1		2								x
			1																								1

	1	e						1		e		1						1			e		1							1		x	2 e								1					e
	1	xdx						1				1		dx				1					1	dx						1		x				\|					1		ln x\|
		xdx					2							dx									x	dx							2					\|							ln x\|
2		1					2		1				x			2				1			x			2					2				1					2						1
		1							1											1															1											1
	1	e2				1			1		lne						1		ln1						1			e2				1						1		1		e2					1		.
		e2									lne								ln1									e2														e2							.
4				4					2							2								4							4						2			4						4
				Следовательно,
		b																e		1							1							1e										1e		1
		b											2					e		1							1							1e										1e		1
			1 y x											dx								x							dx								xdx											dx
			1 y x											dx						2		x							dx						2		xdx											dx
		a														1				2							x								2		1					2			1	x
		a														1																					1								1
	1 x2 e						1 2								1 1									1							1						2		1			2			1 1
					\|				e											lne								ln1							e						e
			2		\|		4		e						4					lne						2		ln1							e						e									2
2			2	1			4								4	2										2					4								4						4					2
				1

1e2 1.

4 4

Задачи для контрольных заданий

4.01 а) Вычислить площадь фигуры, ограниченной линиями y 4 x2 , y 0.

б)Вычислить длину дуги кривой 9y2 4x3 между точками O 0;0 и A3;2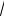3 .

4.02а) Вычислить площадь фигуры, ограниченной линиями y x2 2x 2, y 0, x 0, x 3 .

б) Вычислить длину дуги кривой y 1 x2 1 между точками пересечения и с осью Ox. 2

4.03а) Вычислить площадь фигуры, ограниченной линиями y x2 7x 10 2 x 3 , y 0, x 3 .

б) Вычислить длину дуги кривой x2 2y 3 0 между точками ее пересечения с осью

Ox.

4.04 а) Вычислить площадь фигуры, ограниченной линиями

y 1 , x e, x e2, y 0 . x

б) Вычислить длину дуги кривой y2 x3отсеченной прямой 3x 4 0.

4.05а) Вычислить площадь фигуры, ограниченной линиями y 1 ex, x 0, x 4, y 0.

б) Вычислить длину дуги кривой y2 (x 1)3 между точками A(2; 1)и B(5; 8).

4.06а) Вычислить площадь фигуры, ограниченной линиями y 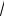x, x 4, y 0.

б) Вычислить длину дуги параболы y x3 от начала координат до точки B 4;8 . 4.07 а) Вычислить площадь фигуры, ограниченной линиями

y	1	, y 0, x 1, x 2.
	x2

б) Вычислить длину дуги кривой y ln xот x 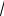3 до x 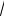8 . 4.08 а) Вычислить площадь фигуры, ограниченной линиями


y cos2x	0 x		, y 0, x 0.

		4

б) Вычислить длину дуги y 1 ex e x от x 0 до x 1. 2

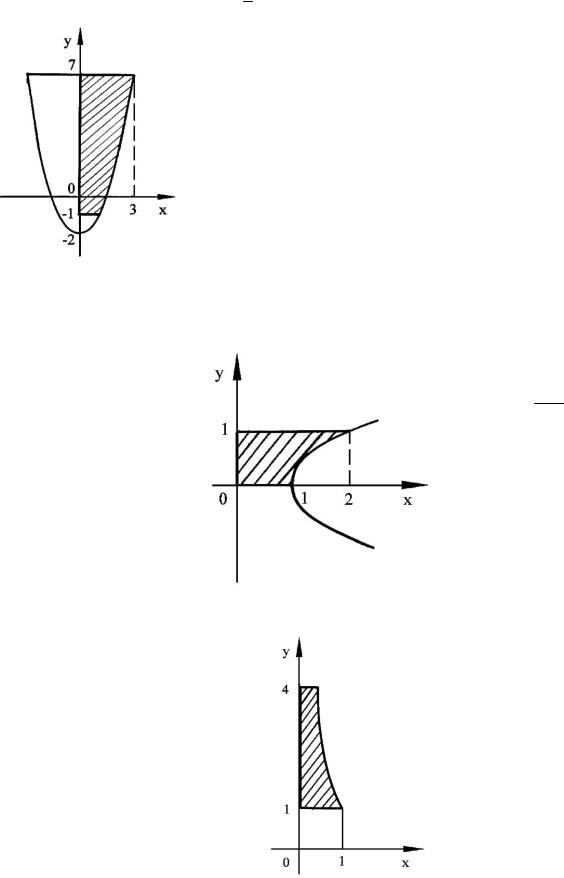
4.09 а) Вычислить площадь фигуры, ограниченной линиями y x2 2 x 0 ,

y 1, y 7, x 0.

4.10 а) Вычислить площадь фигуры, ограниченной линиями

y 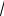x 1, y 1,

y 0, x 0.

		Рис.11
б) Вычислить длину дуги кривой y2 x3от x 0			до x 1 ( y 0).
4.11 а) Вычислить площадь фигуры,
ограниченной линиями
y	1	, y 1,

	x2
y 4,x 0.

Рис.12

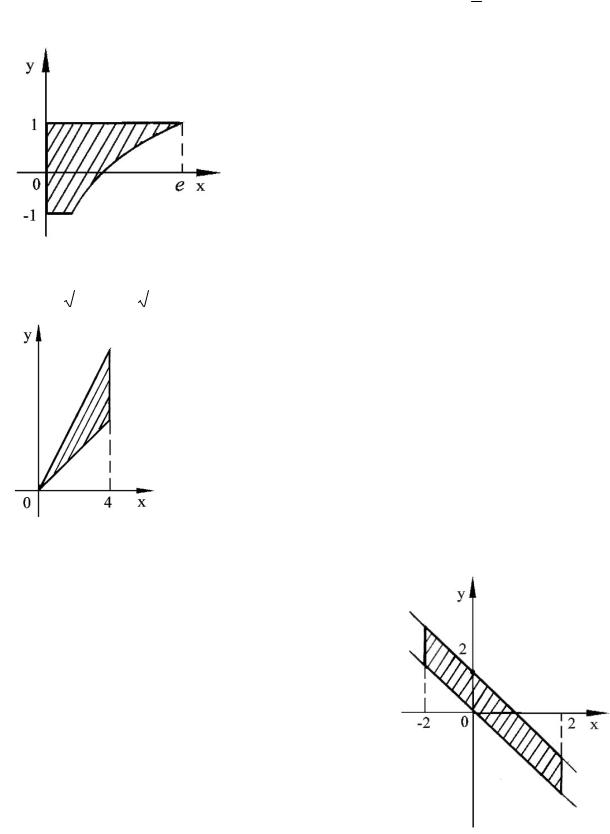
б) Вычислить длину дуги кривой y ln1 x2 от x 0 до x 1 . 4

4.12 а) Вычислить площадь фигуры, ограниченной линиями y ln x,x 0,

y 1,y 1.

		Рис.13					3
				б) Вычислить длину дуги кривой y	1	x2	2		от
					1			2
								2
			3
x	2	до x	7	.

4.13 а) Вычислить площадь фигуры, ограниченной линиями y x,y 2x,

x 4.

Рис.14

б) Вычислить длину дуги кривой y 10 ln x2 1 от x 2 до

x5.

4.14а) Вычислить площадь фигуры, ограниченной линиями

yx,y 2 x, x 2,x 4.

Рис.15

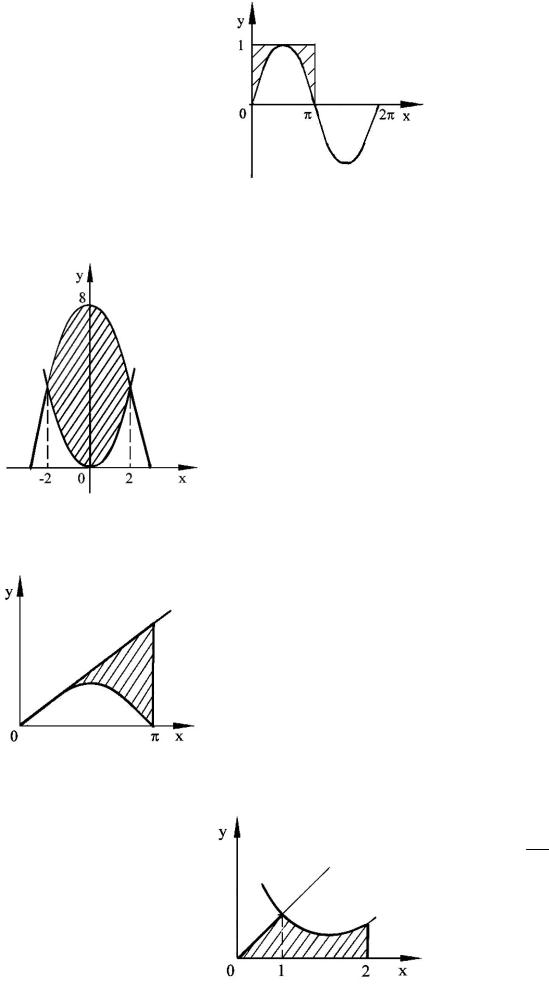
4.15 а) Вычислить площадь фигуры, ограниченной линиями

y sin x, y 1,

x 0,x .

Рис.16
б) Вычислить длину дуги кривой y 1 lncosxот x 0	до x	.

	6

4.16 а) Вычислить площадь фигуры, ограниченной линиями y x2, y 8 x2.

Рис.17

б) Вычислить длину дуги кривой y 2lncos0.5x от x 0

до x .

4.17 а) Вычислить площадь фигуры, ограниченной линиями

y sin x,y x,

x .

б) Вычислить длину дуги кривой y 4 2lnsin0.5x от

Рис.18

x 0.75 до x 1.5 .

4.18 а) Вычислить площадь фигуры, ограниченной линиями

y 1 , y x, x2

x 3.

Pис.19

4.19 а) Вычислить площадь фигуры, ограниченной линиями

y	1	,y	1	,
	x2		x2

x 3,x 1.

Рис.20
б) Вычислить длину дуги кривой y	2	lnsin(0.5 x)	от x 0.5	до x 1.5.

4.20 а) Вычислить площадь фигуры, ограниченной линиями

y x2 , y x2 1, 2

x 1,x 1.

Рис.21	б) Вычислить длину дуги кривой y 0.25x2 0.5ln x
	от x 2	до x 4.
	4.21 а) Вычислить площадь фигуры, ограниченной линиями
		y sin x,

		y cosx	0 x		,
		y cosx	0 x		,
				2

y 0.

Рис.22

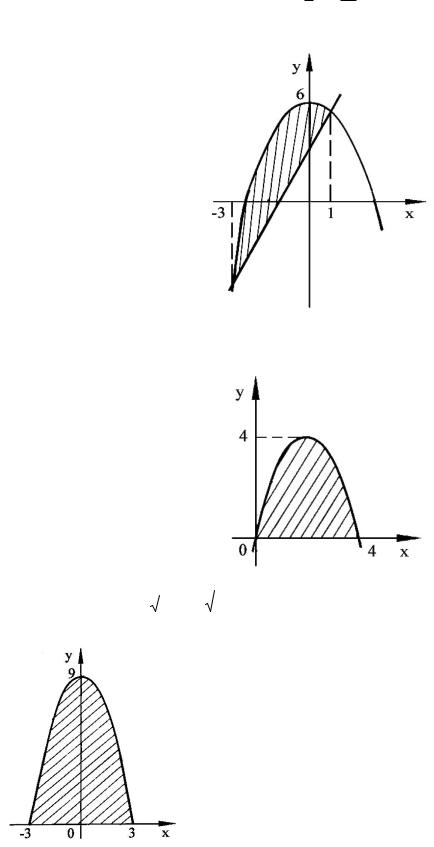
x x

б) Вычислить длину дуги кривой y e2 e 2 от x 0 до x 2.

4.22 а) Вычислить площадь фигуры, ограниченной линиями

y x2 6,

y 2x 3.

Рис.23

б) Вычислить длину дуги кривой y 0.25x2 0.5ln x от x 1 до x 2.

4.23 а) Вычислить площадь фигуры, ограниченной линиями

y 4x x2,x 0.

							Рис.24	б) Вычислить длину дуги
	2			2				б) Вычислить длину дуги
					4
кривой y		x 4				x3	от x 0 до x = 2.
			x
	5		x
	5		3

4.24 а) Вычислить площадь фигуры, ограниченной линиями y 9 x2, y 0.

Рис.25

б) Вычислить длину дуги кривой y 2lnsin0.5x от x 0.5

до x .

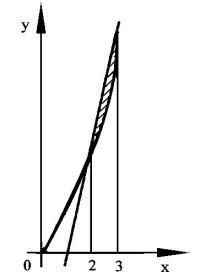
4.25 а) Вычислить площадь фигуры, ограниченной линиями y x2,5x y 6 0.

б) Вычислить длину дуги кривой x2 2y 3 0 между

Рис.26

точками ее пересечения с осью Ox.

Вопросы для самопроверки

1.Как определяется первообразная функции и неопределенный интеграл?

2.Привести основные формулы интегрирования табличных функций.

3.Каким свойствам удовлетворяет неопределенный интеграл?

4.Замена переменных в неопределенном интеграле.

5.Приемы интегрирования некоторых тригонометрических выражений.

6.Интегрирование рациональных дробей.

7.Выведите формулу интегрирования по частям.

8.Как определяется определенный интеграл по формуле Ньютона-Лейбница?

9.Как вычислить площадь криволинейной трапеции?

10.Доказать теорему о среднем для определенного интеграла.

11.Что такое интегральная сумма?

12.Дать определение определенного интеграла через предел интегральной суммы.

13.Сформулировать свойства определенного интеграла.

14.Покажите на примерах формулы интегрирования по частям и замены переменных в определенном интеграле.

15.Как вычисляется несобственный интеграл с бесконечными пределами?

16.Признак сходимости.

17.Как вычисляется несобственный интеграл от функции, имеющей бесконечный разрыв?

18.Признак сходимости.

Глава 2. Дифференциальные уравнения

§1. Дифференциальные уравнения первого порядка

Решение различных задач методом систематического моделирования сводится к отысканию неизвестной функции из уравнения, содержащего независимую переменную, искомую функцию и производные этой функции. Такое уравнение называется дифференциальным.

Определение. Решением дифференциального уравнения называется всякая функция, которая обращает данное уравнение в тождество. Рассмотрим задачу, приводящую к дифференциальному уравнению.

Пример 1. Найти функцию, график которой обладает тем свойством, что отрезок любой касательной, заключенной между осями координат, делится пополам в точке касания.

Решение. Пусть y f x – искомая функция, а M x, y – произвольная точка кривой, определяемой этим уравнением; предположим для определенности, что кривая расположена в первой четверти (рис.27). По условию задачи имеем BM MA, а следовательно, OP PA x .

Из рис.27 видно, что tg PAM MP , т.е. tg 180 y ,

PA x

или tg y . x

Учитывая, что tg есть угловой коэффициент касательной, который в точке

Рис.27

M x,y равен

y , получаем дифференциальное уравнение

(2.1)

Решением уравнения (2.1) является всякая функция вида

(2.2)

Где с– постоянная. В самом деле, заменив в уравнении (2.1) y

его значением из равенства

(2.2), получим

т.е.

Следовательно, равенство (2.2) определяет множество функций, обладающих указанным в задаче свойством. Графики этих функций представляют собой семейство гипербол (рис.28).

			В	дальнейшем				рассмот-
	рим еще ряд примеров, которые
	показывают,				каким			мощным
	математическим аппаратом яв-
	ляются				дифференциальные
	уравнения при решении раз-
	личных			и	весьма		непростых
	практических задач.							Диффе-
			Определение.
	ренциальным уравнением назы-
	вается уравнение,						содержащее
	независимую					переменную			x,
Рис.28	искомую функцию						y	и ее про-
	изводные			y ,		y ,		,	y n .
Символически дифференциальное уравнение записывается так :		n	0.
									(2.3)
F x,y, y , , y

Определение. Порядком дифференциального уравнения называется наибольший поря-

док производных, входящих в данное уравнение.

Определение. Дифференциальным уравнением первого порядка называется уравнение


вида			F x,y, y 0.					(2.4)
			F x,y, y 0.					(2.4)
Разрешая уравнение (2.4) относительно производной y , если это возможно, получим
			y f x,y .					(2.5)
Рассмотренный выше пример показывает, что дифференциальное уравнение имеет, во-
обще говоря, бесконечное множество решений.
При различных значениях постоянной С равенство
			y	C		,		(2.6)
			y			,		(2.6)
				x
определяет различные решения уравнения
			y		y		.	(2.7)
			y				.	(2.7)
					x
Например,		непосредственной подстановкой можно убедиться, что						функции
y 1/x	C 1 ,	y 3/x	C 3 являются решениями уравнения (2.1).

Таким образом, каждому дифференциальному уравнению соответствует, как правило, бесконечная совокупность его решений.

Определение. Всякое отдельно взятое решение дифференциального уравнения называется его частным решением. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную интегральную кривую.

Определение. Функция y (x,C) представляет общее решение дифференциального уравнения (2.4) или (2.5), если при любом значении C эта функция является решением уравнения (2.4) или (2.5) и любое его частное решение может быть получено из y x,C при некотором значении постоянной C.

Иногда не удается получить решение дифференциального уравнения в явной форме

y x или	y x,C , а получают их в неявной форме, т.е. решение задается формулой ви-
да	Ф x, y 0, или Ф x, y,C 0.	(2.8)

<<< < Предыдущая 1 2 34 / 184 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.11.20191.57 Mб5кратные интегр..doc
#
02.05.2015202.24 Кб4кредит.doc
#
02.05.20156.95 Mб244КСС 2013 - на рецензию.doc
#
17.12.2018113.57 Кб5Культурология,родненькая.docx
#
02.05.2015828.18 Кб17культурология.rtf
#
10.03.20166.64 Mб32Курс высшей математики.pdf
#
02.05.201514.85 Mб209Курс лекций по начерталке.doc
#
29.07.2019218.62 Кб0Курс моих лекций по психологии и пед.doc
#
26.11.2019229.89 Кб9курс. глина.doc
#
02.05.2015511.49 Кб17курсавик 1.doc
#
02.05.20151.57 Mб35Курсач Руппель.doc