Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Курс высшей математики

.pdf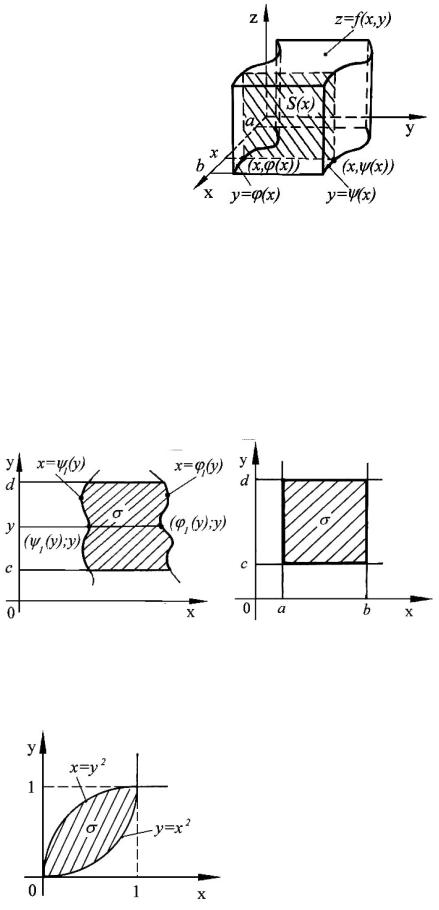

Скачиваний:

Добавлен:

10.03.2016

Размер:

6.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

	b x				b x
f x;y dxdy		f x;y dy dx			dx f x;y dy.			(3.9)
		x			a x
	a	x			a x
					Заметим, что в случае
			вычисления			объема		цилинд-
			рических			тел	интеграл
			x
				f x; y dy		дает	площадь
			x
			S x поперечного сечения
			нашего тела (рис.37), следова-
			тельно, весь объем V будет
Рис.37
b	b x			b	x
		f						(3.10)
V S x dx		f	x;y dy dx dx f x;y dy.					(3.10)
a	a x			a	x

Если же область есть простая область вида 2, то всякая прямая, параллельная оси 0x и проходящая внутри отрезка

a;b , пересекает границу в двух точках: 1 y ;y и 1 y ;y (рис.38). Двойной интеграл по такой области вычисляется по формуле

f x; y dxdy dy

1 y

f x; y dx .	(3.11)
1 y

Наиболее простой вид формулы (9.3) и (11.3) при-

нимают в случае прямоугольной области , ограниченной прямыми x a, x b, y c, y d (рис.39):

		f x; y dxdy	d	b	f x; y dx
		f x; y dxdy	dy		f x; y dx
		.	c	a	(3.12)
Рис.38	Рис.39	.			(3.12)
		Следует	заметить, что

если область не является простой областью, то ее разбивают на конечное число простых об-

ластей 1, 2 , …, n	и при вычислении двойного интеграла по области используют третье
свойство двойного интеграла.			x
	Пример 1. Вычислить двойной интеграл		x	dxdy ,
	Пример 1. Вычислить двойной интеграл		y	dxdy ,
			y

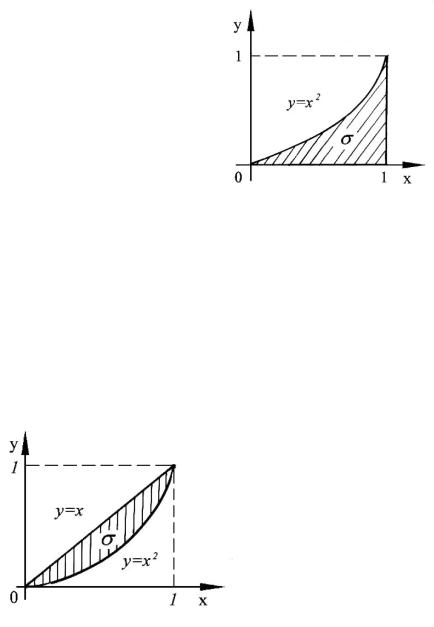
	если область ограничена параболами	y x2	и	x y2
	(рис.40).
	Решение. Область ( см. рис.40) – простая (вида 1).
	Она ограничена снизу кривой x x2,	сверху –		кривой
	61

Рис.40

x y2 , т.е.												y					x		или x x2 (перед радикалом ставим только знак “+”, так как область
находится в I квадранте, где																															y 0); при любом фиксированном значении x из отрезка 0;1																																																	y
меняется от y x2 до																							y								. Поэтому по формуле (3.9) при																																	f x; y							x	имеем
																											x																																												x
																											x																																												y
																																																																							y
											1													1																						1																	1
											1		x											1									x													1									x								1
		x			dxdy										x		dy			dx					x											1		dy		dx									xln y \|							dx x ln												ln x2 dx
		x													x																					1																															x
																																				y																															x
		y													y																	x2				y																		x2									0
												0 x2												0								x2														0								x2									0
1		1																					1			3																				3 1													3					1					1			1 1			dx
x							ln x 2ln x							dx									x							ln xdx																			xln					xdx											x2 ln x \|								x2
0		2																					0			2																				2			0										2					2					0			2	0		x
0																							0																										0																				0				0
	3							1						1 1														3										1			x	2 1							3 1 3
										1 ln1								xdx																										\|												. Замечание Интеграл																		xln xdx взят ме-
								2		1 ln1				2				xdx																										\|												. Замечание Интеграл																		xln xdx взят ме-
	2							2						2				0											2									2		2				0					4 2 8
																		0																										0
тодом интегрирования по частям, причем при подстановке нижнего предела использовался тот
факт, что																																															1
																ln x																															1
																																															x
lim x2 ln x lim																						lim				ln x												lim									x
lim x2 ln x lim																						lim																lim
x 0												x 0						1					x 0								1								x 0										2



																		x	2																													x3
																			2
																																2
																										x
lim										x3			1		lim x2										1				0					0.
lim															lim x2														0					0.
				x 0 2x									2 x 0												2																															x
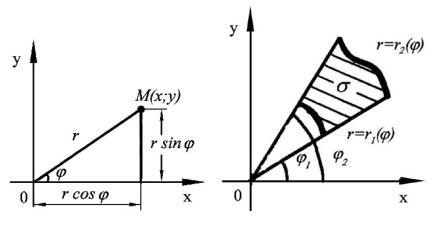
								Пример 2. Вычислить двойной интеграл																																																x	dxdy,						если область											ограничена слева
								Пример 2. Вычислить двойной интеграл																																																2	dxdy,						если область											ограничена слева
																																																								2

																																								кривой x 2 sin y,																			справа прямой													x 0			и с боков пря-
																																								мыми y 0,														y 2 .
																																																Решение. Область (рис.41) является простой (ви-
																																								да 2). При любом фиксированном																																y из отрезка 0;2									x
																																								меняется от														x 0, до									x 2 sin y.									Поэтому по формуле
																																								(3.11) имеем:
																																											x									2 2 sin y								x							2			x	2 2 siny					2					2
																																											x		dxdy															x		dx dy								x			\|	dy			2 sin y					dy
																																													dxdy															2		dx dy							4				\|	dy						4		dy
																																												2												0				2						0			4				0		0					4
																																																					0			0										0							0		0
																																									2 4 4sin y sin2 y																								2									1 cos2y
																																																													dy					1 sin y													dy
																																																						4							dy					1 sin y									4 2				dy
												Рис.41																														0												4										0											4 2
																																									2								1									cos2y									92						2					12
																																												1							sin y													dy					dy sin ydy											cos2ydy
																																												1							sin y								8					dy					dy sin ydy								8			cos2ydy
																																										0							8										8							8			0				0				8			0
																																										0																											0				0							0
		9	y\|2						cosy\|2										1			sin t\|4													9		2 0 cos2 cos0
			y\|2						cosy\|2													sin t\|4															2 0 cos2 cos0
	8						0					0							16					0											8
		1				sin				4 sin 0											9		2 1 1																	1		0 0										9		.
	16					sin				4 sin 0													2 1 1																	16		0 0												.
	16																			8																				16										4

		Замечание.Интеграл cos2ydy				взят методом подстановки t 2y, тогда	dt 2dy или
	1				0
dy	1	dt. При изменении			y от 0 до 2	t меняется от 0 до 4 . Следовательно,
dy		dt. При изменении			y от 0 до 2	t меняется от 0 до 4 . Следовательно,
2
2			1	4
cos2ydy				cost dt.
cos2ydy			2	cost dt.
0			2	0
0				0

Пример 3. Вычисляется объем цилиндрического тела, ограниченного снизу областью, указанной на рис.42, и сверху – плоскостью z x y .

Рис.42

1		x	2	y	2		x	2	1			1			2		1		x4
xy\|						\|		dx		x x	2		x	2		dx		x3		dx
xy\|						\|		dx		x x	2	2	x	2		dx		x3	2	dx
	0			2 0					0			2					0		2
0									0								0

Решение. Область интегрирования ограничена снизу кривой x 0, сверху

– кривой x x2. Спроецировав на ось 0x, получим отрезок 0;1 . Следовательно, 0 x 1. По формуле (3.10)

при f x;y x y	имеем:
	1	x2
V x y dxdy			x	y dy
					dx
	0		0

1		1	1	x	4	\|1	1		x	5	\|1		1	1		1	1		1		1
x3dx		1	x4dx	x			1		x				1	1		1	1		1		1	.
x3dx			x4dx	4			4							4			4					.
0	2		0	4		0	4	5			0	4		4	5		4	20		5
0			0																					y x
	Пример 4. Вычислить массу пластинки, ограниченной прямой																							y x	и параболой
y x2	(рис.43), если плотность распределения массы выражается функцией (x, y) x 2y.
												Решение. Область интегрирования												ограничена снизу
												кривой x x2, сверху –											кривой x x, спроецировав,
												на			ось		0x,			получим			отрезок 0;1 . Следовательно,
												0 x 1. По формуле (3.8) при
													f x;y x;y x 2y
												имеем:
																					1 x			1 x	x

												m x 2y dxdy x											2y dy dx x dy 2 ydy
			Рис.43																		0 x2			0 x2	x2
			Рис.43

1	x			y	2		x			1			2
xy\|	x	2	2			\|	x	2	dx		x x x2	x2	x2	dx
xy\|		2	2	2		\|		2	dx		x x x2	x2	x2	dx
				2						0
0										0

1	x2 x3 x2 x4											1				1			1
									dx 2 x2dx x3dx x4dx
0		x3			x3			x5				0				0			0
2			\|1			\|1			\|1		2		1		1		2	.

	3		0	3		0	5		0	3		3		5		15

§2. Замена переменных в двойном интеграле

При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть

u u u,v ,

v v u,v	(3.13)

функции, определенные на всей плоскости x0y или в некоторой ее области и имеющие непрерывные частные производные в области . Допустим также, что систему уравнений (3.9) можно однозначно разрешить относительно x и y:

	x x u,v ,	(3.14)

тогда каждой точке M x,y	y y u,v ,
	из области будет взаимно однозначно соответствовать пара чи-

сел u,v , называемых криволинейными интегралами этой точки. Если область расположена в той части плоскости x0y, в которой введены криволинейные координаты u , v, то справедлива следующая формула:

f x,y dxdy f x u,v ,y u,v		J u,v		dudv,	(3.15)

где - область изменения криволинейных координат

u и v, отвечающая

области , а

J u,v преобразования (3.14):

J u,v

u v

v u

В частности, в полярных координатах формула (3.14) имеет вид (рис.44)

x rcos ,

(3.16)

y rsin .

y к полярным

Система (3.16) осуществляет переход от прямоугольных координат x

координатам r и при условии, что полюс помещен в начале координат и полярная ось на-

правлена вдоль оси 0x (рис.45). В этом случае

r фор-

мула (3.15) принимает вид

f x,y dxdy f rcos ,rsin rd dr

Если область огра-

ничена лучами,

образующими

с полярной осью углы 1 и

1 2 ,

кривыми

r r1

r r2

Рис.44 Рис.45

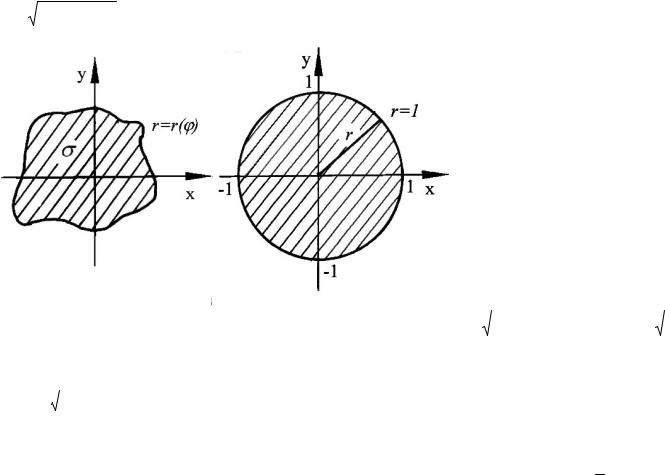
r1 r2 (см. рис. 45), то соответствующие этой области полярные координаты изменяются в пределах

2 1;r1 r r2

и тогда

f x,y dxdy d

f rcos ,rsin rdr .

(3.17)

Если область охватывает начало координат, то

f x, y dxdy d

f rcos ,rsin rdr ,

(3.18)

где r r полярное уравнение кривой, ограничивающее область (рис.46).

Формулы (3.17) и (3.18) очень удобно использовать при решении задач, когда область

есть круг или сектор круга.

Пример 1. Вычислить двойной интеграл

1 x2 y2 dxdy , если область ограничена окружностью x2 y2 1 (рис.47).

Решение. Область

есть круг радиуса 1 с цен-

трами в начале координат.

Введем полярные координа-

ты. В полярных координатах

уравнение

окружности

при-

мет

вид

rcos 2 rsin 2 1,

или

r2 cos2 r2sin2 1

(см.

формулы (3.18)), т.е.

r2 1

или r 1.

Тогда по формуле

(3.18) получаем:

Рис.46

Рис.47

2 1

1 x

dxdy

1 rcos

0 0

2 1								2 1							1
2 1								2 1							1
						2								2
			1 r			2	rdr d			1 r				2	2 rdr
			1 r				rdr d			1 r					2 rdr		d
								0		0
0 0								0		0
					1						1		1														2
					1								1														2
	1 2			0				1 2 t2						0					1 2		0	1		1		2			1	2
	1 2			0				1 2 t2						0					1 2		0	1		1		2			1	2
				t2 dt d										\|		d							d					d		\|0

	2							2		1									2
	2	0		1				2	0	1		1		1					2	0	1.5	1.5		2		3	0		3

										2									1
										2
															1
		Замечание. Интеграл													1 r			2				взят	методом		замены				переменной.
																		2	2
																				rdr
															0

2 .

Положим

1 r2 t. При r 0 получим t 1, а при r 1 t 0. Изменению переменой r от r 0 до r 1 соответствует изменение переменной t от t 1 до t 0.

d 1 r2 dt , или		2rdr dt ,				откуда dr			dt	. Подставляя полученные выражения в
d 1 r2 dt , или		2rdr dt ,				откуда dr				. Подставляя полученные выражения в
								1	2r
1		1					0	1
интеграл, получим	1 r 2			r dr		1	t 2 dt .
			2			1
			2			2
0						2	1
0							1
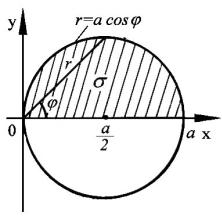
Пример 2. Вычислить двойной интеграл y dxdy , если область ограничена верхней

					половиной дуги окружности x2 y2 ax и отрезком оси 0x
					от точки с абсциссой, равной 0 до точки с абсциссой, равной
					a (рис.48).
							Решение. Введем полярные координаты. Тогда урав-
					нение окружности примет вид rcos 2 rsin 2 arcos ;
					r2 cos2 r2 sin2 arcos ;
					r2 cos2 sin2 arcos ; r2 1 arcos или окончатель-
					но имеем r acos .
							Найдем область определения этой функции. Так как
Рис.48									r 0, то acos 0, то есть
					по определению							.
					по определению							.
									2		2

Верхняя часть дуги окружности лежит в первой четверти, для которой меняется в пределах


																														acos										acos
																												2		acos									2	acos
от 0 до							. По формуле (3.17) имеем ydxdy																									rsin rdr					d sin				r	2dr d
от 0 до							. По формуле (3.17) имеем ydxdy																									rsin rdr					d sin				r	2dr d
			2																													0								0
																												0				0							0	0

						3										3			3							3
2					r	3						2			a	3	cos		3						a	3	2
sin					r			\|acos d sin							a		cos					d			a			cos3 d cos
sin								\|acos d sin									3					d						cos3 d cos
0			3						0			0					3							3			0
0												0															0
														4
	a	3		cos					4		a	3 cos						cos			4		0		a	3					4	4		a	3
		3							4			3 cos				2					4					3					4	4			3
										\|2						2													0				1			.		Пример		3.	Вычислить
										\|2			4																					12		.		Пример		3.	Вычислить
3							4 0				3		4							4				3						4		4		12

объем тела, ограниченного плоскостью z 0 и параболоидом z 3 x2 y2 (рис.49).

Решение. Сверху данное тело (см.рис.49) ограничено параболоидом z 3 x2 y2, поэтому, воспользовавшись формулой (3.10) для вычисления объема цилиндрического тела, ограниченного плоскостью плоскости x0y, имеем

V f x, y dxdy 3 x2 y2 dxdy.

Область (рис.50) есть круг, его границу получим подстановкой z 0 в уравнение z 3 x2 y2 .

Рис.49

Рис.50

			3 r		cos				rdr					3 r		rdr
2		3		2		2		2			2		3		2
							sin
										d							d
0	0										0	0

Введем полярные координаты. Тогда уравнение окружности примет вид

rcos 2 rsin 2 3; r2 cos2 sin2 3; r2 3; r 3 . Угол меняется от 0 до 2 .

Учитывая симметрию тела относительно плоскостей x0z и y0z , воспользовавшись формулой (3.10) , найдем:


V	2		3	2	2

				3 rcos	rsin	rdr
4
	0	0


2					3				3						2							2			r	4
2					3				3						2							2				4		3
			3	rdr r3dr								d						3		r			\|	3			\|	3	d
			3	rdr r3dr								d						3					\|	3			\|		d
				0			0														2		0	4			0
	0			0			0									0
						2					4

2												2					9					9				9 2			9		9

				3				3																						\|2
			3									d											d					d				.
			3									d											d					d				.
				2			4									2						4				4			4	0	8
0				2			4					0				2						4				4		0	4		8
0												0																0
				Следовательно, V												9			.
				Следовательно, V															.
															2
				Пример 4. Вычислить двойной интеграл
		4 x2 y2								dxdy, если область														ограничена линиями: дугой окружности x2 y2 4 и
														x. x 0 (рис.51).
прямыми y x , y
прямыми y x , y													3
																																Решение. Введем поляр-
																																ные координаты. Тогда уравне-
																																ние окружности примет				вид:
																																rcos 2	rsin 2 4;
																																r2 cos2 sin2 4; r2				4;
																																r 2. Найдем угол между пря-
																																мой y			x и осью 0x. В по-
																																мой y		3	x и осью 0x. В по-
																																лярных координатах уравнение
																																прямой			примет	вид:

Рис.51

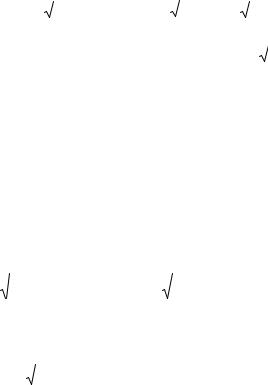
rsin				rcos ;			sin						; tg		;			.
			3				sin				3			3
			3								3			3
							cos								3
	Значит угол между прямой y																x и осью 0x равен						. Найдем угол между прямой
																3
																3					3
																					3
y x и осью 0x. В полярных координатах данное уравнение примет вид:
	rsin rcos ;							sin				1; tg 1;							.
								cos							4
	Значит угол равен									.
	Значит угол равен									.
								4
	Таким образом получим пределы изменения угла от																					до			. По формуле (3.17) име-
ем:	Таким образом получим пределы изменения угла от																				4	до		6	. По формуле (3.17) име-
																					4			6


								2
						3
		2			2	3								2	2
	4 x	2	y		2	dxdy								2	2
	4 x		y			dxdy			4 rcos						rsin					rdr d
								0
						4

	3	2																				3		1		2					1
	3	2								2												3				2				2	1
										2																				2									2
						4 r					rdr d																				2			d 4 r						d
						4 r					rdr d																				2			d 4 r						d
																								2
																								2
		0																								0
	4																					4
												1			1																		3
										2																					2
			3																					3
			3		4 r																			3		2 4 r									\|2d
1					4 r												\|2d 1									2 4 r									\|2d
												2																				2
																	0																		0
		2						1	1								0						2						3						0
								1																					3
							2																				2
				4			2																		4		2
														3					3

		2 3																								2	3									16 3
											2
																			2
																			2
					4 2											4				d							8 d										d
		3												2												3										3
		3																								3										3

			4																								4									4
			4																								4									4
							16											16										16								4


													3
																																						.
							3																								12							.
							3											3			3				4		3				12					9
													4

M x,y равен

y , получаем дифференциальное уравнение

(2.1)

Решением уравнения (2.1) является всякая функция вида

(2.2)

Где с– постоянная. В самом деле, заменив в уравнении (2.1) y

его значением из равенства

(2.2), получим

т.е.

Следовательно, равенство (2.2) определяет множество функций, обладающих указанным

взадаче свойством. Графики этих функций представляют собой семейство гипербол (рис.28).

Вдальнейшем рассмотрим еще ряд примеров, которые показывают, каким мощным математическим аппаратом являются дифференциальные уравнения при решении различных и весьма непростых практических задач.

Определение. Диффе-

ренциальным уравнением назы-

вается уравнение, содержащее независимую переменную x, искомую функцию y и ее про-

изводные y ,			y ,	, y n .
Символически дифференциальное уравнение записывается так :	n	0.
	n			(2.3)
F x,y, y , , y				(2.3)

Определение. Порядком дифференциального уравнения называется наибольший поря-

док производных, входящих в данное уравнение.

Определение. Дифференциальным уравнением первого порядка называется уравнение


вида
F x,y, y 0.					(2.4)
Разрешая уравнение (2.4) относительно производной y , если это возможно, получим
y f x,y .					(2.5)
Рассмотренный выше пример показывает, что дифференциальное уравнение имеет, во-
обще говоря, бесконечное множество решений.
При различных значениях постоянной С равенство
y	C		,		(2.6)

	x
определяет различные решения уравнения
y		y		.	(2.7)

		x

Например,		непосредственной подстановкой		можно убедиться, что функции
y 1/x	C 1 ,	y 3/x	C 3 являются решениями	уравнения (2.1).

Таким образом, каждому дифференциальному уравнению соответствует, как правило, бесконечная совокупность его решений.

Определение. Всякое отдельно взятое решение дифференциального уравнения называется его частным решением. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой семейство кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную интегральную кривую.

Определение. Функция y (x,C) представляет общее решение дифференциального уравнения (2.4) или (2.5), если при любом значении C эта функция является решением уравнения (2.4) или (2.5) и любое его частное решение может быть получено из y x,C при неко-

тором значении постоянной C.
Иногда не удается получить решение дифференциального уравнения в явной форме
y x или y x,C , а получают их в неявной форме, т.е. решение задается формулой ви-
да
Ф x, y 0, или Ф x, y,C 0.	(2.8)
Определение. Выражение Ф x, y 0, или Ф x, y,C 0 в этом случае называют инте-
гралом (частным, общим) дифференциального уравнения.
При решении конкретных задач часто необходимо выделить из всей совокупности ре-

шений дифференциального уравнения то частное решение, которое является ответом на поставленный вопрос. Для того, чтобы из всей совокупности решений выделить отдельную инте-

гральную кривую, задают так называемое начальное условие.
В случае дифференциальных уравнений первого порядка (2.5) под начальными условия-
ми для его решения y y x понимают условия, состоящие в том, что	y y0	при x x0 , т.е.
y x0 y0,		(2.9)
где x0 и y0 – заданные числа (начальные данные) такие, что при	x x0	и y y0 функция
имеет смысл, т.е. существует f x0, y0 .
Определение. Задача нахождения частного решения дифференциального уравнения,
удовлетворяющего заданным начальным условиям, называется задачей Коши.
В случае дифференциального уравнения первого порядка задача Коши формулируется

следующим образом: найти решение y y x уравнения y f x, y , удовлетворяющее при за-

данных начальных данных x0, y0 начальному условию			y x0 y0 , или,	в другой записи,
yx x	y0, где x0, y0 – заданные числа.
0	Пусть даны начальные данные x0 2, y0	3, и	требуется найти	частное решение

y y x уравнения (2.7), удовлетворяющее начальному условию y 2 3. Выше показано, что функция (2.6) при любом C является решением уравнения (2.7).

Подставим в формулу (2.6) начальные данные x 2, y 3, найдем 3 C/2, т.е. C 6. Таким образом, искомым частным решением уравнения (2.7) является функция y 6/2.

Геометрически решение, удовлетворяющее начальному условию y x0 y0 , представляет ин-

тегральную кривую, проходящую через данную точку x0,y0 .

Так, общее решение y C/x уравнения y y/x определяет семейство равносторонних гипербол (см. рис.28). Частное решение y 6/x определяет гиперболу, проходящую через точку (2;3).

Рассмотрим различные типы дифференциальных уравнений первого порядка.

<<< < Предыдущая 1 2 3 4 5 67 / 187 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.11.20191.57 Mб7кратные интегр..doc
#
02.05.2015202.24 Кб5кредит.doc
#
02.05.20156.95 Mб253КСС 2013 - на рецензию.doc
#
17.12.2018113.57 Кб6Культурология,родненькая.docx
#
02.05.2015828.18 Кб20культурология.rtf
#
10.03.20166.64 Mб35Курс высшей математики.pdf
#
02.05.201514.85 Mб213Курс лекций по начерталке.doc
#
29.07.2019218.62 Кб4Курс моих лекций по психологии и пед.doc
#
26.11.2019229.89 Кб13курс. глина.doc
#
02.05.2015511.49 Кб19курсавик 1.doc
#
01.03.202547.12 Кб0курсач по метрологии.docx

1		x	2	y	2		x	2	1			1			2		1		x4
xy\|						\|		dx		x x	2		x	2		dx		x3		dx
xy\|						\|		dx		x x	2	2	x	2		dx		x3	2	dx
	0			2 0					0			2					0		2
0									0								0

1		x	2	y	2		x	2	1			1			2		1		x4
xy\|						\|		dx		x x	2		x	2		dx		x3		dx
xy\|						\|		dx		x x	2	2	x	2		dx		x3	2	dx
	0			2 0					0			2					0		2
0									0								0

1		x	2	y	2		x	2	1			1			2		1		x4
xy\|						\|		dx		x x	2		x	2		dx		x3		dx
xy\|						\|		dx		x x	2	2	x	2		dx		x3	2	dx
	0			2 0					0			2					0		2
0									0								0