
Курс высшей математики
.pdf
7
б) ln x 5 dx;
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) x x2 34 dx. |
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
2.09 а) |
|
cos3 |
x dx; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0,25 arctgx |
|||||||||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0,25 1 x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
xsin x2 dx. |
||||||||||||||
в) |
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.11 а) |
|
ecos x sin xdx; |
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
x |
|
|
|
|
|
|||||||
б) |
|
|
|
|
|
|
|
|
dx; |
|||||||||
|
|
|
2 |
|
||||||||||||||
|
|
|
cos |
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
cosxdx |
|||||||||
в) |
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
2sin x 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4dx
2.13а) 3 x2 3x 2 ;
|
1 |
|
|
|
|
|
|
|
||
б) |
|
|
xe xdx; |
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
в) |
|
|
ctgxdx |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
12 |
|
|
dx |
|
|
|
|||
2.15 а) |
|
|
|
|
|
|
; |
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
sin2 |
|
|||
|
0 |
|
|
x |
|
|
||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
6 |
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
б) |
5 |
cosx |
sin x dx ; |
||||
|
0 |
|
|
|
|
|
|
|
1 |
|
|
ex |
|
|
|
в) |
|
|
|
|
|
dx. |
|
1 e |
x |
||||||
|
0 |
|
|
|
|||
1ex dx
2.10а) 0 ex 5 ;
|
e |
|
|
|
|
|
|
|
|
|
|
|
б) |
x5 ln xdx; |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
6x 5 |
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
. |
|
|
3x2 5x 12 |
|||||||||||
|
1 |
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2.12 а) 3ex3 x2 dx; |
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
б) xe 5x 1dx; |
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|||||||
в) |
|
|
|
|
cos 4x |
|
|
|
dx. |
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
12 |
|
|
|
|
|
|||||
|
|
1 |
|
|
dx |
|
|
|
|
|||
2.14 а) |
|
|
; |
|
|
|||||||
|
|
|
|
|||||||||
|
|
|
0 6 5x x2 |
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
||||
б) xarctgxdx;
0
ln |
3 ex dx |
||
в) |
|
|
. |
|
|||
0 |
1 e2x |
||
4
2.16 а) x x2 9dx;
x2 9dx;
0
21

|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
arctg2xdx ; |
б) |
x 1 ex dx; |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
2x 1 dx |
|
||||
|
2 x dx |
|
2 |
|
|||||||||
в) |
|
|
|
|
. |
в) |
|
|
|
. |
|||
|
2 |
|
|
2 |
x 1 |
||||||||
|
sin |
|
x |
|
0 x |
|
|
||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x5 |
19 dx; |
|
2.17 а) |
2x4 |
|||||
|
1 |
|
|
|
||
|
e |
|
|
|
||
б) xcosxdx; |
||||||
|
1 |
|
|
|
|
|
|
0 |
|
|
|
x3 |
1 |
|
|
|
||||
в) |
x2 e 3 |
dx . |
||||
|
3 |
3 |
|
|
|
|
|
ln2 |
ex dx |
2.19 а) |
0 |
31 2ex ; |
|
2 |
|
|
|
2 |
|
xdx |
|
||||||||||
2.18 а) |
|
|
|
|
|
|
; |
|||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|||||
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) |
|
cos3 xsin xdx ; |
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
xsin x2 dx |
|
||||||||
|
2 |
|
|
|
|
|
||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 5tgx dx |
|
||||||||||||||
|
|
4 |
|
|||||||||||||||
2.20 а) |
|
|
|
|
|
|
|
|
|
|
|
; |
||||||
|
|
|
cos2 x |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
xdx |
|
|
|
|
|
|
|||
б) cosxsin xdx; |
б) |
|
|
; |
||
1 x |
4 |
|||||
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
xdx |
|
|
|
||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|||||||||||||||||
|
1 |
|
|
6 1 x4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln3 |
|
xex2dx; |
|||||||||||||
2.21 а) |
|
|
|
|
|
|
||||||||||||
|
|
|
ln2 |
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
arcsin3 xdx |
|||||||||||||||
б) |
|
|
|
|
|
|
|
; |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
1 x2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
в) |
|
|
|
sin2 x 3sin x 1 cosxdx |
||||||||||||||
2
1 5
2.23 а) ex 1 ex dx ;
0
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
cos2 xsin xdx . |
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
2.22 а) |
|
3 |
cosx |
sin xdx; |
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
б) x2 |
|
x3 8dx; |
||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
. |
в) |
|
sin3 xdx . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
e |
|
dx |
|||||||||||
|
|
ln x |
|||||||||||||
2.24 а) |
|
|
; |
|
|||||||||||
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
22

|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
4 |
|
|
|
|
||
б) sin2xcos3xdx; |
б) cos2 xsin |
2 xdx; |
|||||||||
0 |
|
|
|
|
0 |
|
|
|
|
||
1 |
|
xdx |
1 |
|
|
|
|
||||
|
|
|
|
|
|||||||
в) |
|
|
|
|
в) x x2 1dx. |
||||||
1 x |
2 |
|
|||||||||
0 |
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
ln3 |
|
|
x |
|
|
|
|
|
|
xdx |
2 |
|
3 xdx |
e |
dx |
|
||||||
2.25 а) |
|
б) sin |
в) |
|
. |
||||||||||
|
|
|
|
|
|
||||||||||
1 |
|
1 x4 |
0 |
|
|
0 1 ex |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§3. Несобственные интегралы
1.Интеграл с бесконечными пределами.
Если функция f x интегрируема на любом отрезке a;b , где a b , то полагают
b
f x dx |
lim f x dx. |
(1.8) |
a |
b a |
|
Интеграл f x dx называется сходящимся, если существует предел правой части ра-
a
венства (1.8), и называется расходящимся, если указанный предел не существует. Аналогично, если f (x) интегрируема на любом отрезке a;b , где a b, то полагают
b |
|
b |
|
f x dx |
lim |
f x dx |
(1.9) |
|
a a |
|
|
Наконец, если функция f x интегрируема на любом отрезке a;b числовой оси, то
b
f x dx |
lim |
f x dx. |
(1.10) |
|
b |
a |
|
|
a |
|
|
Сходимость или расходимость несобственных интегралов часто устанавливается с помощью следующих признаков сходимости:
|
|
|
|
|
|
|
|
|
|
|
|
интеграл f x dx; |
a 0 |
|
|
|
|||||||
a |
|
|
|
|
|
|
|
|
|
|
|
а) сходится, если |
|
|
|
|
|
|
|
M |
|
|
|
|
|
f x |
|
|
|
|
|
|
и m 1, |
(1.11) |
|
|
|
|
|||||||||
б) расходится, если |
|
|
|
xm |
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
f x |
|
|
|
и m 1. |
(1.12) |
||||
|
|
|
|||||||||
|
|
|
xm |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Здесь M и m постоянные. |
|
|
|
||||||||
23
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Пример 1. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По определению (1.8) имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
dx |
|
|
b dx |
|
|
|
|
|
b |
|
|
|
|
|
|
|
x 2 1 |
|
b |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
lim |
|
|
|
|
|
|
lim |
|
|
x 2dx lim |
|
|
| |
|
lim |
|
|
|
1 |
lim |
|
|
lim |
1 0 1 1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
b 0 |
|
|
2 |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b b |
b |
|
||||||||||||
1 x |
|
|
1 x |
|
|
1 |
|
|
|
|
|
|
b 2 11 |
|
b |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
Следовательно, интеграл сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
a 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Пример 2. |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По определению (1.8) имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
dx |
|
|
|
b |
|
dx |
|
|
|
|
ln x|b |
lim lnb lna lna . |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
lim |
|
lim |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
a |
x |
|
b |
a |
|
x |
|
|
b |
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Следовательно, интеграл расходится. |
|
|
|
|
|
|
|
|
cos x |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Пример 3. Установить сходимость или расходимость интеграла |
|
|
dx. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
3 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
cosx |
|
|
cosx |
|
|
1 |
, т.е. подынтегральная функция удовлетворяет |
|||||||||||||||||||||||||||
|
|
|
|
|
Решение. Так как |
|
|
1, то |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
неравенству (1.11) при m 3 1 и M 1. Следовательно, интеграл сходится.
2.Интегралы от неограниченных функций
Если функция f x непрерывна при a x b и имеет бесконечный разрыв в точке
x 1, lim f x dx , то полагают
x a
b |
|
b |
|
f x dx |
lim |
f x dx. |
(1.13) |
a |
0a |
|
|
b
Интеграл f x dx называется сходящимся, если существует предел в правой части ра-
a
венства (1.13), и называется расходящимся, если указанный предел не существует. Аналогично определяется интеграл от функции, имеющий бесконечный разрыв в пра-
вом конце отрезка a;b .
|
b |
|
|
b |
|
|
|
|
f x dx |
lim |
f x dx; 0 . |
|
(1.14) |
||
|
a |
|
0a |
|
|
|
|
Если функция f x непрерывна при a x c, |
c x b и имеет бесконечный разрыв в |
||||||
точке x c, то полагают |
|
|
|
|
|
|
|
b |
|
|
c |
|
b |
|
|
|
f x dx lim |
|
f x dx lim |
f x dx , |
0 . |
(1.15) |
|
a |
0 |
a |
0c |
|
|
||
24

b
Интеграл f x dx называется сходящимся, если оба предела в правой части равенства
a
(1.15) существуют и называется расходящимся, если хотя бы один из указанных пределов не существует.
На практике для решения вопроса о сходимости несобственных интегралов от неограниченных функций часто используются следующие признаки сходимости.
Если функция f x имеет бесконечный разрыв в одном из концов интегрирования
a;b , например в точке x a , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
f x dx : |
|
||||||||||||||||||||||||||||||||||||
то несобственный интеграл |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
а) сходится, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
и m 1; |
(1.16) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
б) расходится, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a m |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
и m 1. |
(1.17) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Здесь M и m постоянные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a m |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
Если же |
|
|
f x |
имеет разрыв во внутренней точке x c интервала (a;b), то интеграл раз- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
бивают на два; от a |
до c и от c до b |
и применяют указанные признаки к каждому из полу- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ченных интегралов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Пример 4. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Решение. Функция |
|
|
|
непрерывна при 0 x 1 и имеет бесконечный разрыв в точке |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
x 0, т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x 0 0 x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Поэтому в силу равенства (1.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
dx |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 1 |
|
|
1 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
lim |
|
|
|
|
|
|
|
lim |
x |
|
2dx |
lim |
|
|
|
|
|
| lim2 |
x| |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x 0 |
|
|
|
x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
lim 2 |
|
|
|
|
|
|
|
|
|
|
|
lim 2 2 lim |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
2 2 0 2. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Значит, интеграл сходится и равен 2. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Пример 5. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Решение. Функция |
1 |
|
|
|
|
непрерывна при 0 x 1 и имеет бесконечный разрыв в |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 x2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
точке x 1, т.к. |
|
|
lim |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 0 |
|
|
1 x2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Поэтому в силу равенства (1.13) имеем
25

1 |
|
dx |
|
lim |
1 |
|
dx |
|
lim arcsin x 1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
| |
|
||
0 |
1 x2 |
|
0 0 |
1 x2 |
|
0 |
0 |
|
|||
|
|
|
|
||||||||
lim arcsin 1 arcsin0 lim |
arcsin 1 lim arcsin0 arcsin1 arcsin 0 |
|
0 |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
Интеграл сходится и равен |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Пример 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x 1 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Решение. Функция |
|
|
|
|
|
|
|
непрерывна при 0 x 1 |
и 1 x 3, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x 1 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
т.к.: lim |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
. Значит в точке x 1 функция имеет |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x 1 0 x 1 2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x 1 0 x 1 2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
бесконечный разрыв. Поэтому в силу равенства (1.15) имеем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
dx |
|
|
|
3 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
0 |
x 1 |
|
0 0 x 1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
2 |
d x 1 |
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
lim x 1 |
|
|
|
|
x 1 |
|
|
|
d x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
lim |
x 1 2 1 |
|1 |
lim |
x 1 2 1 |
|
|3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
2 1 |
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||||||||||||||||||||
lim |
|
|
|
|
| |
|
|
lim |
|
|
|
|
|
| |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
x 1 0 |
|
|
|
|
0 |
|
|
x 1 |
|
1 |
|
|
|
|
|
0 1 1 |
|
|
0 1 |
|
0 3 1 |
|
1 1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
0 1 |
|
|
|
|
0 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
lim |
1 |
1 |
1 |
|
lim |
|
1 |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Следовательно, интеграл расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 cos xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Пример 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Решение. Функция |
|
|
имеет бесконечный разрыв в |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
1 |
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
точке x 0, т.к. |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
.Но для |
|
x 0 |
|
|
|
|
|
|
|
|
|
, т.к. |
|
1. Значит эта функ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
x |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
ция удовлетворяет неравенству (15.1) при m |
1 иM 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2
Следовательно, интеграл сходится.
Задачи для контрольных заданий
Вычислить несобственный интеграл или доказать его расходимость.
26
|
|
|
|
|
|
|
|
dx |
|
|
|
|
ln(x 1) |
|
|
|||||||||||||||||||||||||||||
3.01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
3.02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(x 1)2 4 |
|
1 |
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
x4 |
|
|
|
|
2 |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3.03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
3.04 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xln x |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 x5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3.05 |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
3.06 |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
|
4 xln |
|
|
x |
|
|
|
|
0 4 x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
3.07 |
|
|
|
|
|
|
|
|
|
|
dx; |
3.08 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
4) |
3 |
|
|||||||||||||||||||||||
|
11 x |
|
|
|
|
|
|
|
|
|
|
2 (x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
3.09 |
|
|
|
|
|
|
|
|
|
|
dx; |
3.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
11 x6 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
4 x2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
1 dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
3.12 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(x 2)2 |
9 |
|
0 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3.13 |
x e x2 dx; |
3.14 |
|
|
arctgx |
|
dx; |
|||||||||||||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 dx |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||||
3.15 |
|
|
|
|
|
|
dx ; |
|
|
|
3.16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||||
|
1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 (x 2) |
|
|
|
|
|
|
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|||||||||||||||||
3.17 |
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
3.18 |
|
|
|
|
|
|
|
|
|
|
dx; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|||||||||||||||||||||||||||
|
0 3 9 x2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
e |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.19 |
|
|
|
|
|
dx; |
|
|
|
3.20 xln x dx; |
||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctgx |
|
|
||||||||||||||||||||||||
3.21 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
3.22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|||||||||||||||||||||
|
0 9 x |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|||||||
3.23 |
x2 x2 dx; |
|
|
|
3.24 |
|
|
|
|
|
|
|
dx; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
x 3 |
|
|||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.25 |
|
|
|
|
|
|
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
01 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
§4. Приложения интегрального исчисления
В этом параграфе при помощи интегрального исчисления будет решен ряд задач. Площадь S фигуры, ограниченной графиком функции y f x (сверху), y g x (сни-
зу) и прямыми x a, x b подсчитывается по формуле
27
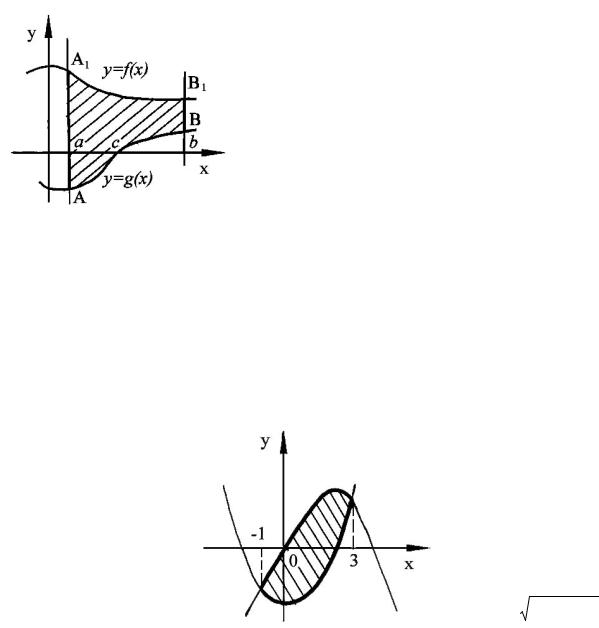
b
S f x g x dx (1.18)
b
Действительно, в силу геометрического смысла определенного интеграла (см. равенство(1.18)) имеем (рис.4)
b
f x dx S aA1B1b
a
|
b |
|
и |
g x dx S cBd S aAc , |
поэтому |
|
a |
|
Рис.4 |
b |
b |
b |
|
|
f x g x dx |
f x dx g x dx S aA1B1b ScBb S aAc S |
, |
a |
a |
b |
|
|
|
|
как это видно из рисунка. |
|
|
|
Пример 1. Вычислить площадь между параболами y 4x x2 и y x2 6 (рис.5). Решение. Сначала найдем точки пересечения парабол, для чего решим систему уравне-
ний
y ax x2;
y x2 6,
|
|
|
|
|
Рис.5 |
|
Тогда |
по |
формуле |
(1.18) |
искомая |
3 |
4x x2 |
|
3 |
|
|
S |
x2 6 dx 6 4x 2x2 dx |
||||
1 |
|
1 |
|
|
|
т.е. найдем точки на плоскости, координаты которых удовлетворяют одновременно уравнениям обеих парабол. Из этой системы
x2 6 4x x2 ,
2x2 4x 6 0, x2 2x 3 0 и
x |
2 22 4 3 |
|
2 4 |
|
|
||
1,2 |
2 |
2 |
|
|
|||
или x1 1;x2 3.
площадь S будет равна:
|
|
2 |
2 |
|
3 |
3 |
|
|
|
2 |
2 |
|
|
3 |
|
|
|
|
|
|
|||
|
6x 2x |
|
|
|
x |
|
| |
|
6 3 2 3 |
|
|
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
3 |
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
|
6 1 2 1 2 |
|
2 |
1 3 |
18 |
|
10 |
18 |
10 |
64. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
||||||
|
Пример 2. Вычислить площадь фигуры, ограниченной линиями y x2, |
y |
, y 0, |
||||||||||||||||||||
|
x2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 x 0 .
28
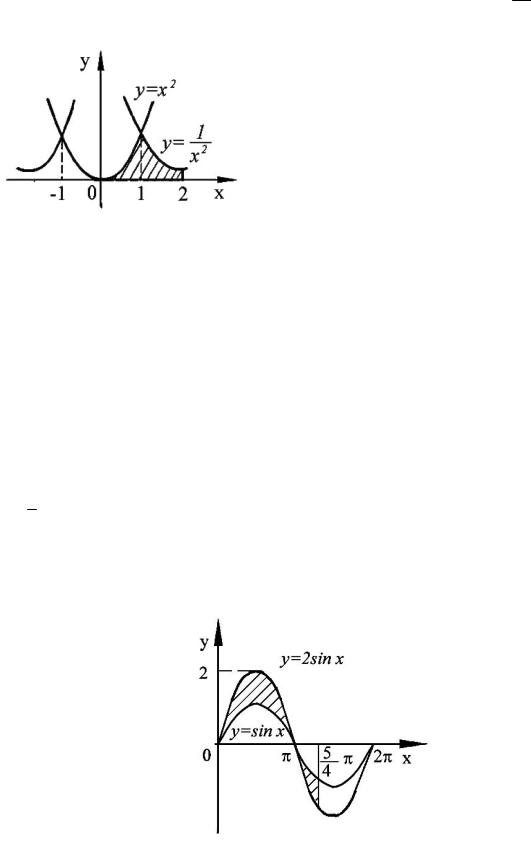
Решение. Сначала найдем точки пересечения кривых y x2 и y 1 , для чего решим x2
систему уравнений
y x2; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
y |
. |
|
|
|
|
||
|
|
|
|||||
|
|
x2 |
|
|
|||
Из |
этой системы x2 |
1 |
, |
x4 1 или |
x 1, |
||
|
|||||||
|
|
|
|
x2 |
|
1 |
|
|
|
|
|
|
|
||
x2 1.
Таким образом, заданная фигура (рис.6) является Рис.6 криволинейной трапецией, ограниченной сверху графиком
функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x2, 0 x 1, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
, |
1 x 2. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
По формуле (1.18) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
1 |
|
|
|
2 |
|
dx |
|
|
x |
2 1 1 2 |
|
|
|
|
x |
2 1 |
|
x |
2 1 2 |
|||||||||||
S f x dx x2dx |
|
|
|
|
|
| x 2dx |
|
|
| |
|
|
|
| |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0 |
|
|
|
0 |
|
|
|
1 x2 |
|
2 1 |
0 1 |
|
|
|
|
|
|
3 0 |
|
2 1 |
1 |
|||||||||||||
1 |
|
|
|
1 |
2 |
1 |
|
|
|
1 1 |
1 1 |
|
|
|
5 |
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
|
|
|
x |
1 |
3 |
|
2 1 3 2 |
6 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Вычислить площадь фигуры, ограниченной линиями y sin x , y 2 sin x, x 5 , x 0.
4 |
|
|
|
|
|
|
|
|
Решение. Искомая площадь S равна сумме площадей S1 и S2 |
двух фигур, первая из ко- |
|||||||
торых ограничена линиями |
y sin x , |
y 2sin x, |
x 0, |
x , вторая ограничена линия- |
||||
ми y sinx , y 2sin x, x , |
x |
5 |
(рис.7). |
|
|
|
|
|
|
|
|
|
|
||||
|
4 |
|
|
|
|
|
Для вычисления площа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дей S1 и S2 применим форму- |
||
|
|
|
|
|
|
лу(1.17): |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
S1 2sin x sin x dx |
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin xdx cosx | |
||
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
cos cos0 |
||
|
|
|
|
Рис.7 |
|
1 1 1 1 2. |
||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 |
sin x 2sin x dx |
|
29
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
5 |
|
|
|
|
|
|
|
2 |
|
||
sin xdx cosx |
| cos |
cos |
|
|
1. |
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2,293. |
|
|
|
||||
|
|
Тогда S S |
S |
2 |
2 |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перейдем теперь к следующей задаче – определению длины линии. В школьном курсе давалось определение длины окружности как предела периметров правильных вписанных многоугольников при неограниченном удвоении числа их сторон.
Теперь мы обобщим это понятие на любые линии. Для этого выделим из приведенного выше определения самое существенное: в линию (окружность) вписывается
ломаная, берется длина этой ломаной, а затем увеличивается число звеньев ломаной так, что длины всех звеньев стремятся к нулю (удваиваются числа сторон). Из этого и будем исходить.
Определение. Длиной линии называется предел
lim длина АА1А2 Аn 1B , |
|
0 |
|
где AA1A2 An 1B – вписанная в L ломаная, а – длина наибольшего из звеньев этой лома-
ной (рис.8).
Покажем, что если линия L есть график функции y f x , a x b, имеющей непрерывную производную, то ее длина
b |
|
|
|
|
|
|
1 f |
|
2 |
|
|||
|
(1.20) |
|||||
x |
dx. |
|||||
a
Впишем в линию L ломаную AA1A2 An 1B
(рис.9). Ее вершины имеют координаты: A a; f a ,
A1 x1; f x1 , |
A2 x2; f x2 , |
, |
An 1 xn 1; f xn 1 , |
|
|||||
B b; f b . Подсчитаем длину этой ломаной по фор- |
|
||||||||
муле |
f x1 f a f c1 x1 a , |
a c x1 ,так дли- |
|
||||||
на первого звена равна |
|
|
|
|
|
|
|||
AA |
|
a x 2 f x f a 2 |
|
|
x a 2 |
f c x a 2 |
|
||
1 |
1 |
1 |
|
1 |
1 |
1 |
|
||
1 f c1 2 x1 a , a c1 x1.
Рис.9
|
Аналогично |
|
|
устанавливается, |
|
что |
длина |
второго |
звена |
рав- |
||||||
на A A |
1 f c |
2 |
x |
2 |
x , x |
c |
2 |
x |
2 |
и т.д. и , наконец, длина последнего звена |
|
|||||
1 |
2 |
2 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|||
An 1B 
 1 f cn 2 b xn 1 , xn 1 cn b.
1 f cn 2 b xn 1 , xn 1 cn b.
Следовательно, в силу определения длины линии (формула(1.18)):
30
