
- •5.3.Расчетно-графическая работа ргр5 к4 Кинематика сложного движения точки при переносном вращательном движении
- •5.3.1. Схемы конструкций и исходные данные
- •5.3.2. Указания и план выполнения
- •5.3.3. Пример выполнения расчетно-графической работы к4 сложное движение точки при переносном вращательном движении
- •1. Кинематические характеристики точки м в относительном движении
- •2. Кинематические характеристики точки м в переносном вращательном движении
5.3.3. Пример выполнения расчетно-графической работы к4 сложное движение точки при переносном вращательном движении
Дано : Диск радиусаR=72 м вращается вокруг неподвижной осиOZ, перпендикулярной плоскости диска (XOY) (рис.5.4) и проходит через точкуO (диск вращается в своей плоскости ).
Уравнение вращательного движения диска дано:
 ,
, , , где
, , где .
.
Положительное направление отсчета угла
 показано на рис.5.4 дуговой стрелкой,
направленной против часовой стрелки.
показано на рис.5.4 дуговой стрелкой,
направленной против часовой стрелки.
По ободу диска движется точкаМ, траекторная координата этого движения, отсчитываемая от точки«Н», изменяется согласно уравнению
 =
= + AО
sin
k
t,
где
+ AО
sin
k
t,
где
 ,AО,
k
– постоянные
величины:
,AО,
k
– постоянные
величины:
 =0
м;
=0
м;
AО
=R /2
м, k=
/2
м, k=

 .ОО1
= L
=
.ОО1
= L
=
 м.
м.
Определить: абсолютную скорость
и абсолютное ускорение (относительно
неподвижной системы координатOXYZ)
точкиМ в момент времени ,
где
,
где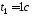 .
.
Рис.5.4.
Решение.
За подвижную систему отсчета (ПСО)
принимаем диск, а связанные с ним оси
координат ─ подвижные оси.
─ подвижные оси.
За абсолютную (неподвижную) систему отсчета (АСО) принимаем подшипникO, а связанные с ним оси координатXOYZ ─ неподвижные оси.
─ Относительное движение −
перемещение точки Мотносительно
диска (ПСО) в подвижной системе
координат по ободу диска, т.е. по окружности
(траекторный или естественный способ
задания движения точки (см.разд..1, табл.
1.1); все кинематические характеристики
этого движения обозначаются с индексом
«r» :
по ободу диска, т.е. по окружности
(траекторный или естественный способ
задания движения точки (см.разд..1, табл.
1.1); все кинематические характеристики
этого движения обозначаются с индексом
«r» : ,
, ,
, .
.
─ Переносное движение − движение
неизменяемой среды, неизменно связанной
с подвижной системой отсчета (диском),
относительно неподвижной системы
отсчета(АСО)
XOYZ− ( вращательное
вокруг осиOZ(см.
разд..2.3)); все кинематические характеристики
этого движения обозначаются с индексом
« »:
»: ,
, ,
, ,
, ,
, .
.
─ Абсолютное движение − перемещение
точки Мотносительно неподвижной
системы отсчета(АСО)
XOYZ;
все кинематические характеристики
этого движения обозначаются с индексом
« »:
»: ,
, .
.

Рис.5.5.
1. Кинематические характеристики точки м в относительном движении
Для этого следует воспользоваться формулами раздела “ Кинематика точки” при траекторном (естественном) способе задания ее движения.
Траекторная координата точки М ,заданная уравнением
 =
= + AО
sin
k
t
,
+ AО
sin
k
t
,
после подстановки – =0
м;AО
=R
=0
м;AО
=R /2
см,, k=
/2
см,, k=

 ,
примет вид
,
примет вид =R
=R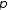 /2·sin(π/6) ·t.
(5.3.1)
/2·sin(π/6) ·t.
(5.3.1)
При t=1с:

 =R
=R /2·sin(π/6) 1=R
/2·sin(π/6) 1=R /2·
1/2 =R
/2·
1/2 =R /4
м .
/4
м .
 окр=2
окр=2 Rм; (
Rм; (
 ) / (
) / ( окр)
= (R
окр)
= (R /4)
/ (2
/4)
/ (2 R)
=1/8
R)
=1/8
 =(1/8)
(
=(1/8)
( окр=360°)
= 45°;
окр=360°)
= 45°;
На рис.5.5 определено положение точки Мна диске в момент времени (а не в произвольном положении, показанном
на рис.5.4) в подвижной (относительной)
системе отсчетапри естественном (траекторном) способе
задания ее движения, при котором
(а не в произвольном положении, показанном
на рис.5.4) в подвижной (относительной)
системе отсчетапри естественном (траекторном) способе
задания ее движения, при котором >O .
>O .
Cкорость точкиМ :  ,
где
,
где
 ─ касательная к траектории в данной
точке, направленная всегда в сторону
возрастания траекторной координатыs
;
─ касательная к траектории в данной
точке, направленная всегда в сторону
возрастания траекторной координатыs
;
 =
= (5.3.2)
(5.3.2)

 =
6π20,866 = 59,20,866 = 52,3 м/с; так как
=
6π20,866 = 59,20,866 = 52,3 м/с; так как >0, то
>0, то 
 .
.
Ускорение точки М: ,
(5.3.3)
,
(5.3.3)
где
 ─
касательное, а
─
касательное, а ─ нормальное ускорения точки;
─ нормальное ускорения точки;
 =
= ;
(5.3.4)
;
(5.3.4)

 =
-3 0,5= - 15,5м/с2
. Так как
=
-3 0,5= - 15,5м/с2
. Так как  <0,то
<0,то
 .
.
 =
= ;
;
 =
51,32/ 72 = 36,5м/с2,
(5.3.5)
=
51,32/ 72 = 36,5м/с2,
(5.3.5)
где ρ ─ радиус кривизны траектории в данной точке.
Все векторы
 ,
, и
и определены для момента времени
определены для момента времени и изображены на рис.5.4 (без определения
и изображены на рис.5.4 (без определения ).
).
