4.7. Методы вычисления определителей

a) Схема единственного деления Гаусса.

Так как определитель треугольной матрицы равен произведению диагональных элементов, то

,

где - ведущий элемент на шаге номера.

b) Схема Холецкого.

Так как в схеме Холецкого матрица раскладывается в произведение нижней и верхней треугольных матриц, т. е. , то по свойству определителей

.

Так как элементы главной диагонали матрицы равны 1, то. Тогда

.

с) Метод Гаусса с выбором главного элемента.

По свойству определителей вычитание строки из строки не меняет значение определителя. При перестановке строк или столбцов матрицы определитель меняет знак. Так как определитель треугольной матрицы равен произведению диагональных элементов, то после приведения матрицы к верхней треугольной получаем, что

,

где знак определителя зависит от того, четным или нечетным было суммарное количество перестановок строк или столбцов матрицы.

4.8. Методы обращения матриц

Задача нахождения обратной матрицы вплотную примыкает к задаче решения систем линейных алгебраических уравнений вида . Пусть- обратная матрица к матрице. Умножим обе части последнего матричного уравнения слева на матрицу. В результате получим. Откудаили. Таким образом, зная обратную матрицу, можно определить решение системы уравнений.

a) Метод Гаусса.

Используем метод Гаусса для нахождения обратной матрицы. Пусть обратная матрица к матрице

имеет вид .

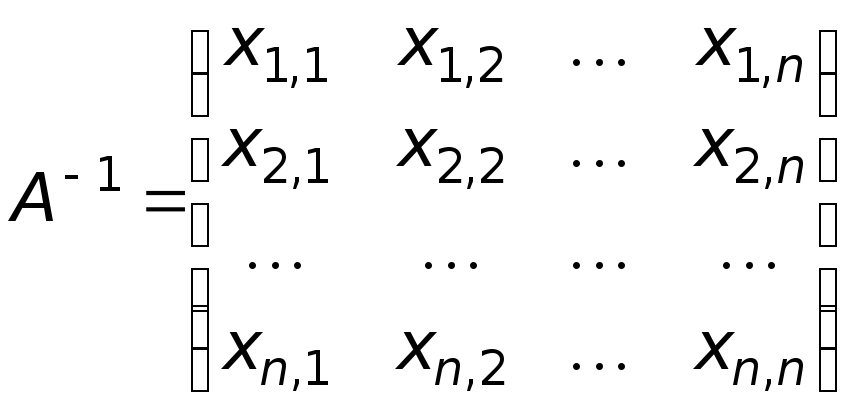Из определения обратной матрицы следует, что , т. е.

=.

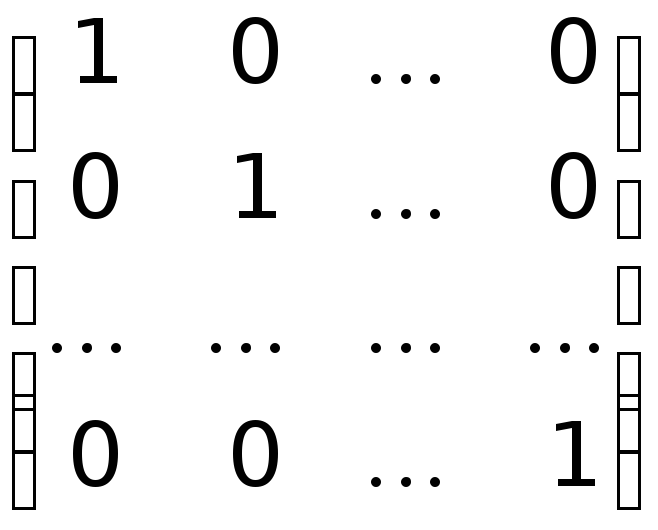Перемножая матрицы в левой части равенства и сравнивая с соответствующими элементами матрицы в правой части, получимсистем линейных алгебраических уравнений снеизвестными вида

,

где вектор -ой системы имеет вид:,, если. Решив всесистем методом Гаусса, получим матрицу.

b) Метод Жордана.

Пусть после -го шага преобразования по методу Жордана матрицаимеет вид

.

Разделим - ю строку матрицына ведущий элементи исключим все внедиагональные элементы- го столбца. После выполнения этой операции приходим к матрице, которая имеет точно такой же вид, что и предыдущая матрица, но с заменой индексана индекс. Матрицыисвязаны соотношением, где матрицаимеет вид

.

Применяя описанный процесс к матрице , получим матрицы, причем,,

,

…………………..

,

.

Но в соответствии с методом Жордана . Отсюда находим

.

Из определения обратной матрицы имеем

Обозначим . Матрицавыражается следующим образом, т. е. переход от матрицык матрицеосуществляется по тем же формулам, что и переход от матрицык матрице. Кроме того, первыестолбцов матрицыи последниестолбцов матрицысовпадают со столбцами единичной матрицы. Это позволяет определять элементы обратной матрицы внутри одного массива. Таким образом, метод Жордана дает простой алгоритм вычисления обратной матрицы без использования дополнительной оперативной памяти. Пусть. Строим последовательно матрицы, вычисляя их коэффициентыпо следующим формулам

Тогда . При этом все вычисления происходят внутри одного массива.

с) Метод отражений.

Метод отражений позволяет преобразовать произвольную невырожденную матрицу в верхнюю треугольную с помощью матриц отражения следующим образом. Тогда после умножения слева на матрицуполучим, что. Из последнего равенства следует, что. Так как матрицаверхняя треугольная, то и матрицабудет верхней треугольной и, значит, может быть легко определена.

Рассмотрим алгоритм обращения верхней треугольной матрицы. Пусть

, .

Тогда и по правилу умножения матриц получаем

, ;

, ,;

, ,,

;

………………………………………………………………………………………………………

, ,,

.

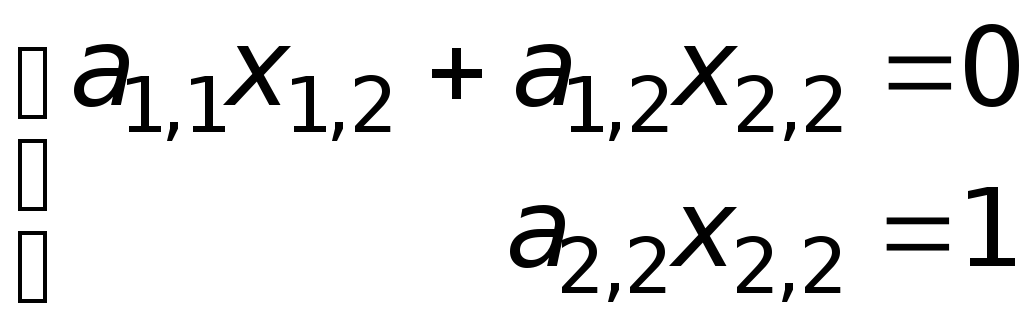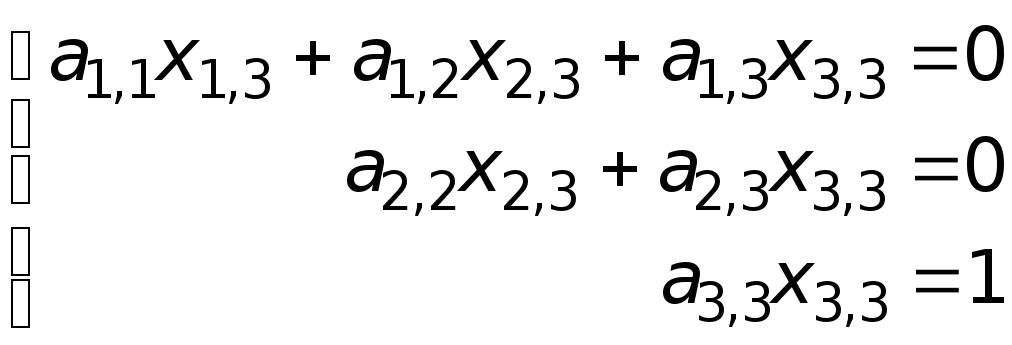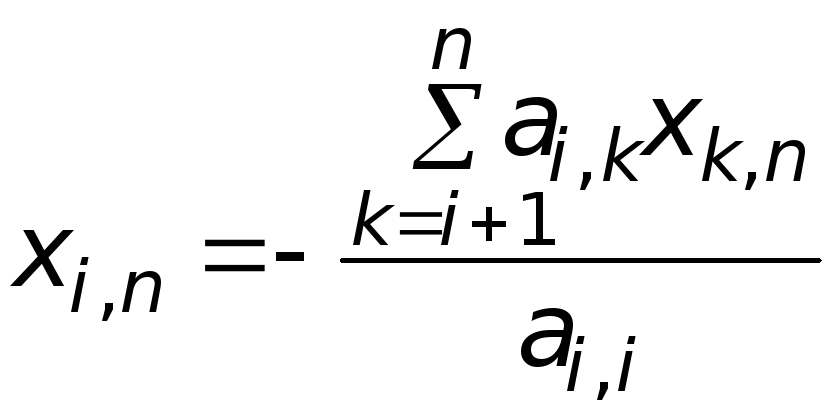ЛЕКЦИЯ № 14

ЛЕКЦИЯ № 15

4.10. Методы решения слау с трехдиагональной матрицей Рассмотрим систему трехточечных уравнений

(4.44)

и предположим, что коэффициенты иотличны от нуля. Матрица этой системы является трехдиагональной и имеет вид

Системы вида (4.44) возникают при трехточечной аппроксимации краевых задач для обыкновенных дифференциальных уравнений второго порядка с постоянными и переменными коэффициентами, а также при реализации разностных схем для уравнений в частных производных. Эффективным методом решения системы (4.44) является метод исключения Гаусса, который приводит к формулам прогонки.

Предположим, что исвязаны рекуррентным соотношением

(4.45)

с неопределенными коэффициентами и.

Подставим в уравнение.

Получим . После приведения подобных имеем

. (4.46)

Подставим теперь (4.45) в (4.46) и преобразуем полученное равенство

,

.

Последнее уравнение справедливо для любых , если

,

.

Отсюда получаем рекуррентную формулу для

, , (4.47)

и рекуррентную формулу для определения

, . (4.48)

В обоих случаях предполагается, что .

Если коэффициенты иизвестны и известно значение, то, двигаясь отк, получим последовательно все. Определим начальные значения для коэффициентови. Для этого используем первое уравнение системы (4.44) и равенство (4.45) при. Имеем

,

.

Сравнивая эти уравнения, получим

, . (4.49)

Используем теперь для определения значения последнее уравнение системы (4.44) и равенство (4.45) при. В результате получим систему уравнений

,

решая которую находим

. (4.50)

Описанный метод решения систем линейных алгебраических уравнений с трехдиагональной матрицей называется методом правой прогонки. Коэффициенты иназываются прогоночными коэффициентами, формулы (4.47)-(4.49) описывают прямой ход метода прогонки, а формулы (4.45) и (4.50) – обратный ход. Для решения системы (4.44) необходимо выполнитьопераций умножения и деления.

Алгоритм метода правой прогонки будет корректен, если в формулах (4.47) и (4.48) отличны от нуля значения . Кроме того, если всепо модулю больше единицы, то может произойти сильное увеличение погрешности, и, еслидостаточно велико, то полученное реальное решение будет значительно отличаться от искомого решения.

Теорема 4.5 (достаточное условие корректности и устойчивости метода прогонки). Пусть коэффициенты системы (4.1) удовлетворяют условиям ,,

, ,,,,

, (4.51)

, , (4.52)

причем хотя бы в одном из неравенств (4.51) или (4.52) выполняется строгое неравенство, т. е. Матрица системы (4.44) имеет диагональное преобладание. Тогда для метода прогонки имеют место неравенства ,,, гарантирующие корректность и устойчивость метода.

Доказательство: Покажем, что из неравенства ,и условий теоремы следует, чтои.

Пусть ,. Тогда

=.

Следовательно, . Кроме того

.

Так как , то неравенствавыполняются для всех. Покажем, что. Если, тои. Значит, если одно из неравенств (4.51) или (4.52) является строгим, то обязательнои

.

Покажем, что метод прогонки при выполнении условий теоремы не приводит к накоплению ошибок округления. Пусть - точное решение системы (4.44), а- искаженное решение, полученное в результате наличия ошибок округления. Тогда из уравнений

и следует, что

, т. е. , гдеи

. Так как для всех, то

.

Это означает, что погрешность вычислений не возрастает в процессе решения системы (4.44), т. е. метод прогонки устойчив.

ЛЕКЦИЯ № 16