
- •4.2 Вычислительная устойчивость методов решения слау
- •4.3 Методы исключения
- •4.3.1 Схема единственного деления
- •4.3.2 Метод Жордана
- •4.3.3 Метод оптимального исключения
- •4.3.4 Метод Гаусса с выбором главного элемента
- •4.4 Методы, основанные на разложении матриц
- •4.4.1. Схема Холецкого
- •4.4.2 Метод квадратного корня
- •4.4.3 Метод отражений
- •4.4.4 Метод вращений
- •4.5 Методы, основанные на построении вспомогательной системы векторов
- •4.5.1 Метод ортогонализации
- •4.5.2 Метод сопряженных градиентов
МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
4.1 Классификация методов решения систем линейных
алгебраических уравнений
К решению систем линейных алгебраических уравнений сводится подавляющее большинство задач вычислительной математики. В настоящее время предложено огромное количество алгоритмов решения таких систем.
Все методы решения
линейных алгебраических уравнений
можно разделить на две большие группы:
прямые и итерационные. В прямых (или
точных) методах решение системы находится
за конечное число арифметических
действий. Итерационные методы позволяют
найти за конечное число итераций
приближенное решение системы с любой
наперед заданной точностью
![]() .
.
Примером прямого метода решения СЛАУ служит метод Крамера, в соответствии с которым
![]() ,
,
![]() .
.
Однако на практике этот метод не используется, так как он требует выполнения очень большого количества арифметических операций. Большая часть существующих прямых методов укладывается в следующую схему. Пусть задана система
![]() (4.1)
(4.1)
линейных
алгебраических уравнений. Умножим обе
части равенства (4.1) слева на такие
матрицы
![]() ,
при которых новая система
,
при которых новая система
![]() (4.2)
(4.2)
равносильна исходной и легко решается. Для этого достаточно, чтобы матрица
![]()
была треугольной или диагональной. Методы, основанные на подобных преобразованиях, составляют в настоящее время самую значительную группу среди численных методов задач алгебры.
Одним
из старейших является метод Гаусса, в
основе которого лежит идея последовательного
исключения неизвестных. Он использует
левые треугольные матрицы
![]() и позволяет свести исходную систему
уравнений к системе с правой треугольной
матрицей. Этот метод легко реализуется
на компьютере, его схема с выбором
главного элемента позволяет решать
системы с произвольной невырожденой
матрицей, а компактная схема – получить
результаты с повышенной точностью.
Среди всех прямых методов метод Гаусса
требует минимального объема вычислений.
и позволяет свести исходную систему
уравнений к системе с правой треугольной
матрицей. Этот метод легко реализуется
на компьютере, его схема с выбором
главного элемента позволяет решать
системы с произвольной невырожденой
матрицей, а компактная схема – получить
результаты с повышенной точностью.
Среди всех прямых методов метод Гаусса
требует минимального объема вычислений.
Непосредственно
к методу Гаусса примыкают метод Жордана
и метод оптимального исключения. Эти
методы используют треугольные матрицы
![]() (как левые, так и правые) и позволяют
привести исходную систему к системе с
диагональной матрицей. Метод оптимального
исключения позволяет при заданном
объеме оперативной памяти решать системы
более высокого порядка, чем метод
Жордана.
(как левые, так и правые) и позволяют
привести исходную систему к системе с
диагональной матрицей. Метод оптимального
исключения позволяет при заданном
объеме оперативной памяти решать системы
более высокого порядка, чем метод
Жордана.
Перечисленные
методы входят в группу методов исключения.
Это название объясняется тем, что при
каждом умножении на матрицу
![]() в матрице системы исключается один или
несколько элементов. Существуют методы
решения систем, которые сочетают в себе
как свойства прямых методов, так и
итерационных. Как итерационные они
построены на минимизации некоторого
функционала, достигающего своего
минимума на решении системы (4.1). Однако
итерации обрываются не позднее чем на
в матрице системы исключается один или
несколько элементов. Существуют методы
решения систем, которые сочетают в себе
как свойства прямых методов, так и
итерационных. Как итерационные они
построены на минимизации некоторого
функционала, достигающего своего
минимума на решении системы (4.1). Однако
итерации обрываются не позднее чем на![]() -ом
шаге (
-ом
шаге (![]() - порядок системы), давая точный ответ.
К таким методам относится метод
сопряженных градиентов.
- порядок системы), давая точный ответ.
К таким методам относится метод
сопряженных градиентов.
4.2 Вычислительная устойчивость методов решения слау
Решение
системы (4.1) задается формулой
![]() .
Влияние ошибок округления может привести
к тому, что в процессе счета будет
получена система уравнений, не равносильная
исходной. Возникает вопрос об устойчивости
метода решения.
.
Влияние ошибок округления может привести
к тому, что в процессе счета будет
получена система уравнений, не равносильная
исходной. Возникает вопрос об устойчивости
метода решения.
Пусть
![]() и
и![]() - заданные величины, а
- заданные величины, а![]() и
и![]() - близкие к ним. Будем рассматривать
- близкие к ним. Будем рассматривать![]() ,
,![]() и
и![]() как дифференциалы. Тогда из формулы
(4.1) имеем
как дифференциалы. Тогда из формулы
(4.1) имеем![]() .
Откуда
.
Откуда![]() .
Отсюда следует, что если элементы
обратной матрицы велики, то незначительная
ошибка в элементах исходной матрицы
или правой части может повлечь за собой
значительное изменение в решении.
Поэтому при выборе метода решения
системы нужно обращать внимание на
условия его устойчивости.
.
Отсюда следует, что если элементы
обратной матрицы велики, то незначительная
ошибка в элементах исходной матрицы
или правой части может повлечь за собой
значительное изменение в решении.
Поэтому при выборе метода решения
системы нужно обращать внимание на
условия его устойчивости.
4.3 Методы исключения
4.3.1 Схема единственного деления
Метод
Гаусса и его модификации основаны на
приведении с помощью элементарных
преобразований исходной системы к
системе верхней треугольной или
диагональной матрицы. В схеме единственного
деления на каждом шаге строка делится
на элемент, стоящий на главной диагонали
(ведущий элемент), и исключаются элементы
под главной диагональю. Предположим,
что
![]() ,
,![]() и
и![]() шагов метода уже сделаны. Тогда на
шагов метода уже сделаны. Тогда на![]() -ом
шаге расчетные формулы имеют вид
-ом
шаге расчетные формулы имеют вид
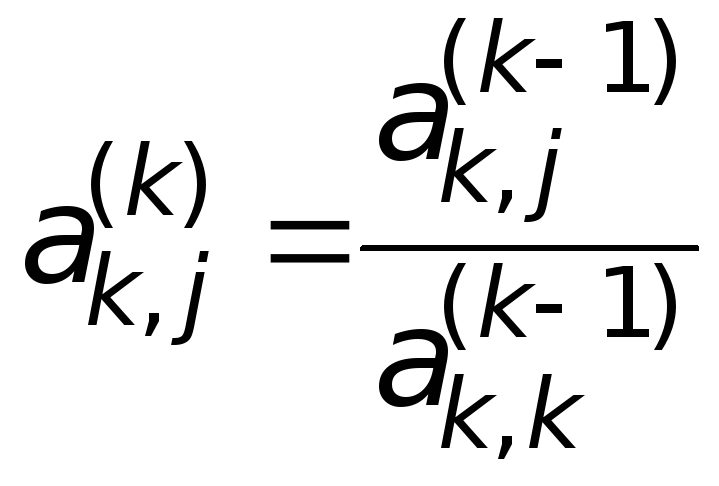 ,
,
![]() ,
(4.3)
,
(4.3)
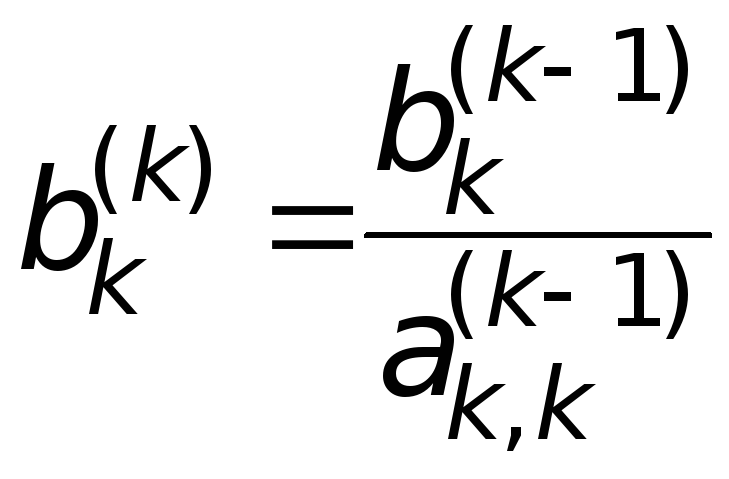 ,
(4.4)
,
(4.4)
![]() ,
(4.5)
,
(4.5)
![]() ,
,
![]() ,
,![]() .
(4.6)
.
(4.6)
После
![]() -го
шага матрица системы принимает вид
-го
шага матрица системы принимает вид
 .
(4.7)
.
(4.7)
Процесс приведения матрицы исходной системы к системе с верхней диагональной матрицей называется прямым ходом метода Гаусса, а процесс получения значений неизвестных – обратным ходом. Неизвестные из преобразованной системы находятся по формулам
![]() ,
,
![]() ,
,![]() .
(4.8)
.
(4.8)
Подсчитаем число арифметических операций, необходимых для решения системы (4.1) по схеме единственного деления. Так как выполнение операций умножения и деления на ЭВМ требует гораздо больше времени, чем выполнение сложений и вычитаний, то подсчитаем только число умножений и делений.
1.
Вычисление коэффициентов
![]() ,
,![]() ,
,![]() по формулам (4.3) требует
по формулам (4.3) требует
![]() делений.
делений.
2.
Вычисление всех коэффициентов
![]() по формулам (4.5) требует
по формулам (4.5) требует
![]()
![]() умножений.
умножений.
Таким образом, вычисление элементов верхней треугольной матрицы требует
![]() операций
умножения и деления.
операций
умножения и деления.
3.
Вычисление правых частей по формулам
(4.4) требует
![]() делений, а нахождение
делений, а нахождение![]() по формулам (6)
по формулам (6)
![]() умножений.
умножений.
Следовательно, для вычисления правых частей необходимо
![]()
операций умножения и деления.
В итоге для осуществления прямого хода метода Гаусса необходимо выполнить
![]() действий.
действий.
4. Для осуществления обратного хода метода Гаусса по формулам (4.8) необходимо выполнить
![]() умножений.
умножений.
Окончательно получаем, что для реализации схемы единственного деления метода Гаусса необходимо выполнить
![]() операций
умножения и деления.
операций
умножения и деления.
После
преобразования исходной системы по
схеме единственного деления получаем
систему вида
![]() ,
где матрица
,
где матрица![]() это матрица (4.7). Подставляя в (4.1) выражение
для
это матрица (4.7). Подставляя в (4.1) выражение
для![]() в виде
в виде![]() приходим к уравнению
приходим к уравнению![]() или, что то же самое, к уравнению
или, что то же самое, к уравнению![]() .
Сопоставляя последнею систему с системой
(4.1) приходим к выводу, что при применении
метода Гаусса матрица
.
Сопоставляя последнею систему с системой
(4.1) приходим к выводу, что при применении
метода Гаусса матрица![]() системы есть произведение нижней
треугольной матрицы
системы есть произведение нижней
треугольной матрицы![]() на верхнюю треугольную матрицу
на верхнюю треугольную матрицу![]() с единичной главной диагональю, т.е.
с единичной главной диагональю, т.е.![]() .
.
ЛЕКЦИЯ № 8
