Консультации
Если в процессе изучения материала или при решении той или иной задачи у студента возникают вопросы, на которые он не может ответить сам, то можно обратиться к преподавателю для получения письменной или устной консультации. В случае письменной консультации в запросе следует, возможно, более точно указать характер затруднения. При этом обязательно следует указать полное название книги, год издания и страницу, где трактуется непонятный для студента вопрос или помещена соответствующая задача.
Типовой пример 1.
Найти неопределенный интеграл:
Решение типового примера.
В подынтегральной функции числитель почленно разделим на знаменатель и воспользуемся известными свойствами неопределенного интеграла:
,
.
а также табличными формулами
;
Типовой пример 2.
Найти
неопределенный интеграл
;
Решение типового примера.
Перейдем в подынтегральном выражении к переменной t, затем найдем интеграл и вернемся к переменной x. Произведем замену переменной,
t=
4+5x,
dt=5dx,
dx=
,
тогда
Типовой пример 3.
Найти
неопределенный интеграл
:
Решение типового примера.
Интеграл находится методом замены переменной.
Введем новую переменную t=2x2-3, выразим подынтегральное выражение через t и найдем первообразную, после чего вернемся к старой переменной x.
.
Типовой пример 4.
Найти
неопределенный интеграл
;
Решение типового примера.
Интеграл определяется методом замены переменной
.
Типовой пример 5.
Найти
неопределенный интеграл
Решение типового примера.
Найдем интеграл методом замены переменной
;
Типовой пример 6
Найти
неопределенный интеграл
.
Решение типового примера.
Применим
формулу интегрирования по частям
.
Интеграл
должен быть проще исходного интеграла
,
определив его, тем самым находят исходный
интеграл.
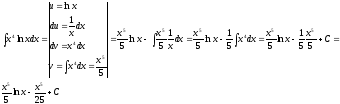
Типовой пример 7.
Вычислить
определенный интеграл
;
Решение типового примера.
Для
вычисления интеграла воспользуемся
формулой интегрирования по частям в
определенном интеграле
и формулой Ньютона- Лейбница
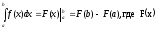- первообразная дляf(x).
Кроме того, следует применять табличные
интегралы
;
;
Типовой пример 8.
Вычислить
определенный интеграл
.
Решение типового примера.
Воспользуемся методом замены переменной в определенном интеграле и формулой Ньютона –Лейбница.
Сделаем замену переменной:
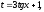
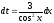
При
x=
0 t=1,
а при x=
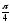t=4.
Типовой пример 9.
Вычислить площадь фигуры, ограниченной линиями: y=x2
x+y-2=0
Решение типового примера.
y=x2 – квадратичная функция, график парабола, вершина в т. О (0,0); ветви направлены вверх.
x+y-2=0; y=-x+2 –линейная функция, график прямая.
Найдем точки пересечения линий:
x1=-2;
x2=1;
y1=4;
y2=1
Схематично изобразим фигуру в прямоугольной системе координат.
Площадь заштрихованной фигуры определяется формулой
S=
гдеa,
b
– абсциссы точек пересечения графиков;
f1 (x)- функция, график которой ограничивает фигуру сверху;
f2 (x)- функция, график которой ограничивает фигуру снизу.
Таким образом
ед2.