Самостоятельная работа

“Теория вероятностей ”

2015

Содержание.

Введение ____________________________________________ 4

Образец решения типового варианта по теории вероятностей___5

Варианты заданий по теории вероятностей__________________ 9

Литература __________________________________________ 18

Введение.

В связи с тем, что по учебной программе при изучении дисциплины “Теория вероятностей и математическая статистика” значительное время отводится на самостоятельную работу студентов, практикуется такая её форма, как типовой расчёт. Типовой расчёт включает в себя наиболее типичные и распространённые практические задания по основным разделам учебной программы.

2. Образец решения типового задания по теории вероятностей.

1. В ящике 10 шаров: 7 черных и 3 белых. Из ящика вынимают 5 шаров. Найти вероятность того. что среди них окажется 3 черных и 2 белых шара.

Решение.

Требуемую вероятность найдем с помощью классической формулы:

Число n - общее число возможных исходов - равно (поскольку порядок шаров безразличен) сочетанию 5 из 10 элементов: n = C

Теперь определим число благоприятных исходов т. Очевидно, что способов, которыми можно вынуть 3 черных шара из 7 и 2 белых шара из 5 равно cсоответственно: Си С.

Поскольку каждая комбинация черных шаров может сочетаться с любой комбинацией белых, всего получится Сспособов.

Получим: Р(А) =

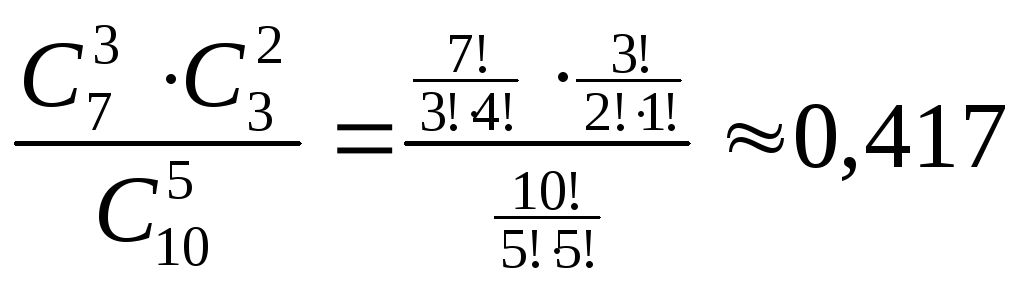
Ответ: Р(А) ≈ 0,42

2. Из колоды в 36 карт наугад вынимают 5 карт. Какова вероятность того, что среди них не будет карты пиковой масти?

Решение.

Как и в предыдущем случае воспользуемся формулой классического подсчета вероятностей

Очевидно, общее количество возможных исходов n равно С

Так как в колоде 27 карт не пиково» масти, то благоприятным исходом можно считать извлечение 5 любых из них. Тогда m = С

Получим: Р(А) =

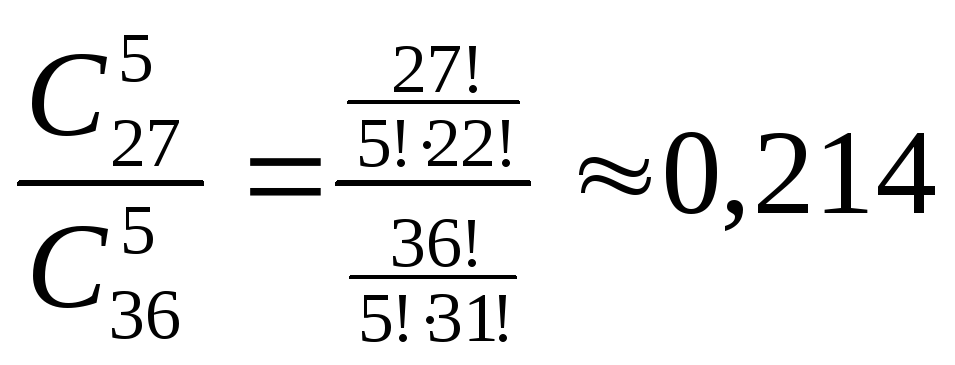
Ответ: Р(А) ≈ 0,214

3. Вероятность обнаружения опечатки на странице книги равна 0,01. Найти вероятность того, что в 500-страничной книге не будет обнаружено опечаток (обнаружение опечаток на различных страницах считать независимыми событиями).

Решение.

Поскольку в условиях независимых испытаний Бернулли вероятность р = 0,01 близка к нулю, а n = 500 велико, применим формулу Пуассона:

P_n(k) = a=500 ∙ 0,01 = 5

Для k = 0 (отсутствие опечаток), получаем: H₅₀₀(0) =

Ответ: Р₅₀₀ ≈ 0,007

4. Узел содержит три независимо работающие детали. Вероятность отказа деталей соответственно равны 0,1; 0,2; 0,3. Найти вероятность отказа учла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Решение.

Для нахождения вероятности события А - отказа узла, найдем сначала вероятность противоположного события Р(Ā), заключающегося в исправной работе всех деталей:

Р(Ā) = (1-0,1)∙(1-0,2)∙(1-0,3) = 0,9∙0,8∙0,7 = 0,504.

Искомая вероятность равна:

Р(А) = 1 - Р(Ā) = 1-0,504 = 0,496

Ответ: Р(А) ≈ 0,496

5. Монета бросается пять раз. Найти вероятность того, что орел выпадет 2 раза.

Решение.

По формуле Бернулли при n = 5, р = 0,5 найдем искомую вероятность:

Ответ: Р₂(2) ≈ 0,01

6. Два завода производят детали, поступающие в магазин. Вероятность выпуска бракованной детали для первого завода равна 0,8, для второго - 0,7. С первого завода поступило в 3 раза больше деталей, чем со второго. Покупатель приобрел годную деталь. Найти вероятность того, что она с первого завода.

Решение.

Этот пример решим по формуле Байеса:

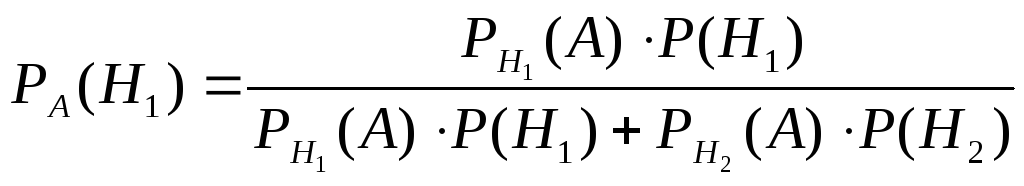
Где события (гипотезы) Н₁ и Н₂ - произвольно выбранная соответственно первом или втором заводе деталь; событие А заключается в том, что деталь годная. Получим:

Ответ: Р_А ≈ 0,77

7. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины, заданной законом распределения:

Х	- 1	2	4
р	0,2	0,3	0,5

Решение.

Сначала найдём математическое ожидание по формуле:

Дисперсию вычислим по формуле:

.

Чтобы найти , составим закон распределения дляв виде таблицы:

Х	1	4	16
р	0,2	0,3	0,5

Тогда .

Получим: .

Находим среднее квадратическое отклонение: .

Ответ: .

7. Случайная величина задана функцией распределения:

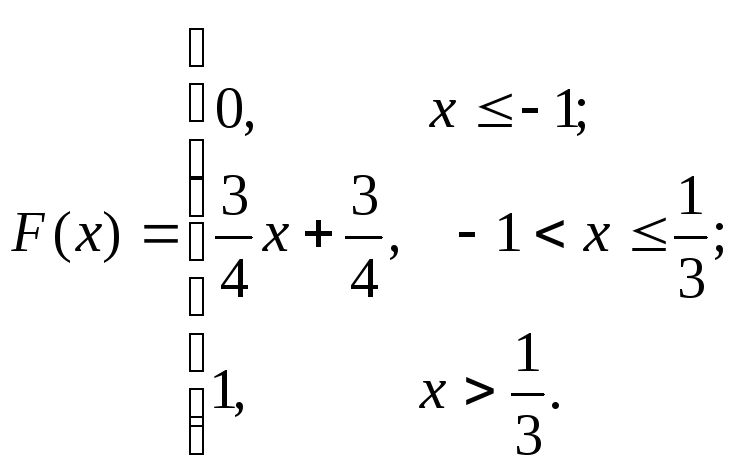
Найти: а) плотность распределения случайной величины; б) вероятность того, что в результате испытания величина примет значение, заключённое в интервале .

Решение.

а) Воспользуемся тем, что плотность распределения является производной от функции распределения: . Получим:

б) Вероятность того, что случайная величина примет значение из некоторого интервала равна приращению её функции распределения на этом интервале:

.

В нашем случае:

.

7. Задана плотность распределения непрерывной случайной величины :

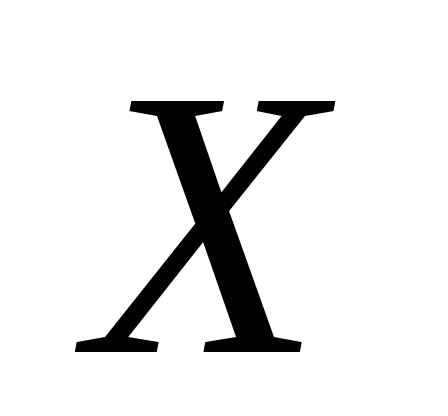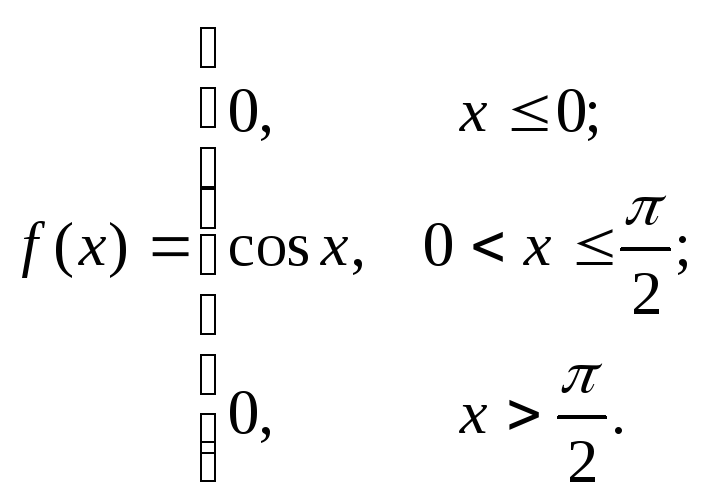
Найти функцию распределения .

Решение.

Используем формулу:

.

Получим: