
- •Самостоятельная работа № 4 Введение в математический анализ
- •Тема 4. Введение в математический анализ.
- •Список литературы
- •Решение типового варианта контрольной работы.
- •Контрольная работа №4. Вариант 1
- •Контрольная работа №4. Вариант 2
- •Контрольная работа №4. Вариант 3
- •Контрольная работа №4. Вариант 4
- •Контрольная работа №4. Вариант 5
- •Контрольная работа №4. Вариант 6
- •Контрольная работа №4. Вариант 7
- •Контрольная работа №4. Вариант 8
- •Контрольная работа №4. Вариант 9
- •Контрольная работа №4. Вариант 10
- •Контрольная работа №4. Вариант 11
- •Контрольная работа №4. Вариант 12
- •Контрольная работа №4. Вариант 13
- •Контрольная работа №4. Вариант 14
- •Контрольная работа №4. Вариант 15
- •Контрольная работа №4. Вариант 16
- •Контрольная работа №4. Вариант 17
- •Контрольная работа №4. Вариант 18
- •Контрольная работа №4. Вариант 19
- •Контрольная работа №4. Вариант 20
- •Контрольная работа №4. Вариант 21
- •Контрольная работа №4. Вариант 22
- •Контрольная работа №4. Вариант 23
- •Контрольная работа №4. Вариант 24
- •Контрольная работа №4. Вариант 25
- •Контрольная работа №4. Вариант 26
- •Контрольная работа №4. Вариант 27
- •Контрольная работа №4. Вариант 28
- •Контрольная работа №4. Вариант 29
- •Контрольная работа №4. Вариант 30
Контрольная работа №4. Вариант 7
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
 ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.

Контрольная работа №4. Вариант 8
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.

Контрольная работа №4. Вариант 9
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
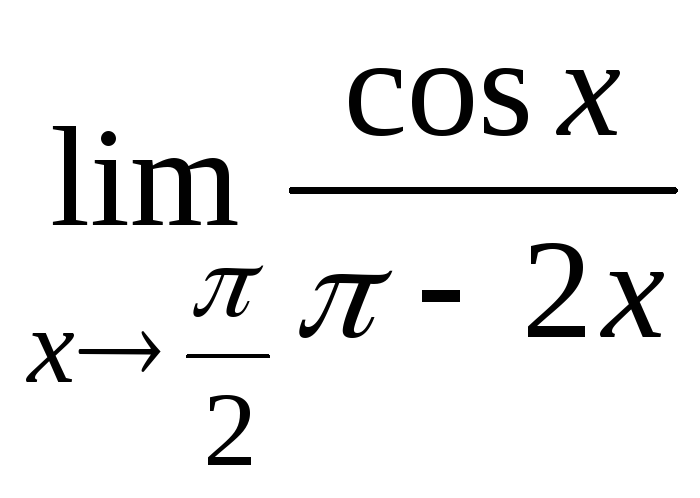 ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.

Контрольная работа №4. Вариант 10
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
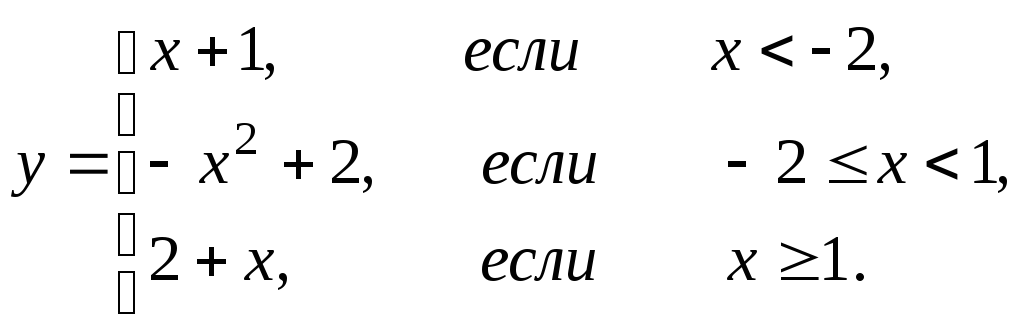
Контрольная работа №4. Вариант 11
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
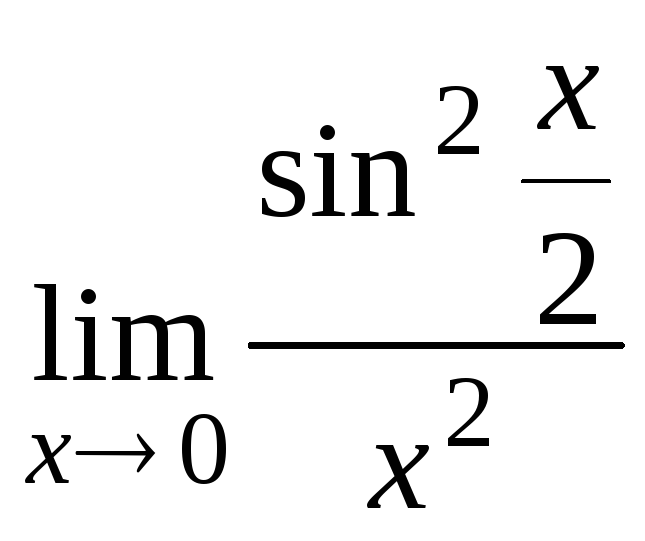 ;
;
д)
 ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.
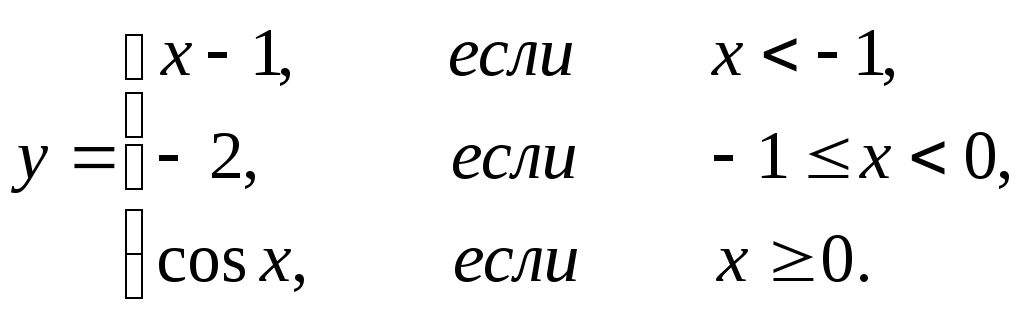
Контрольная работа №4. Вариант 12
Вычислить пределы функций.
а)
![]() ;
;
б)
![]() ;
;
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
![]() .
.
2. Дана функция
![]() и два значения аргумента
и два значения аргумента![]() .
.
Требуется.
1)Найти значение
функции при стремлении аргумента к
каждому из данных значений
![]() ;
;
2) Определить,
является ли функция непрерывной или
разрывной при данных значениях
![]() ;
;
3) Сделать
схематический чертеж в окрестности
точек
![]() и
и![]() .
.
![]() ,
,
![]() .
.
3. Для кусочно-заданной
функции
![]() .
.
Требуется.
1) Найти точки разрыва функции, если они существуют;
2) Найти скачок функции в каждой точке разрыва;
3) Сделать схематический чертеж.

