Задача №2.

Условие задачи №2 несколько различается в зависимости от номера варианта контрольной работы. Приведем решения простейших задач, входящих в это задание.

1) Составить уравнение плоскости, проходящей через точки ,,.

Решение.

Уравнение плоскости, проходящей через точки ,,имеет вид:

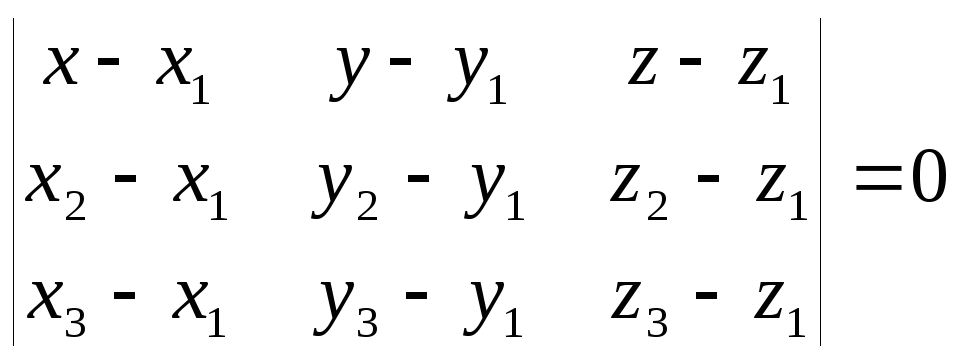(3.7)

Тогда уравнение плоскости в силу уравнения (3.7) имеет вид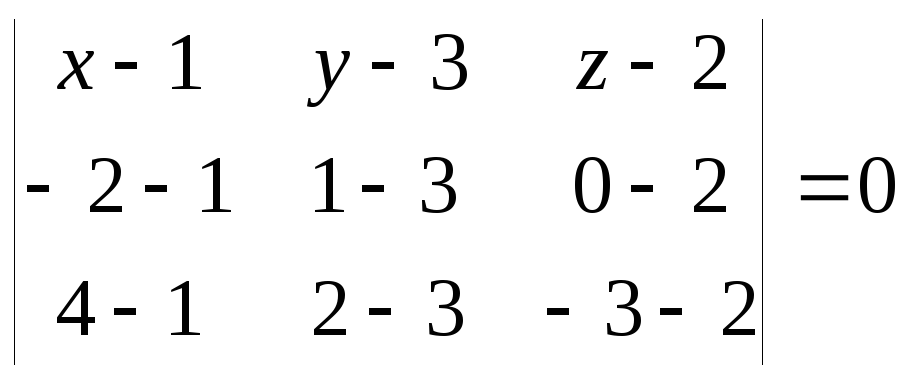или.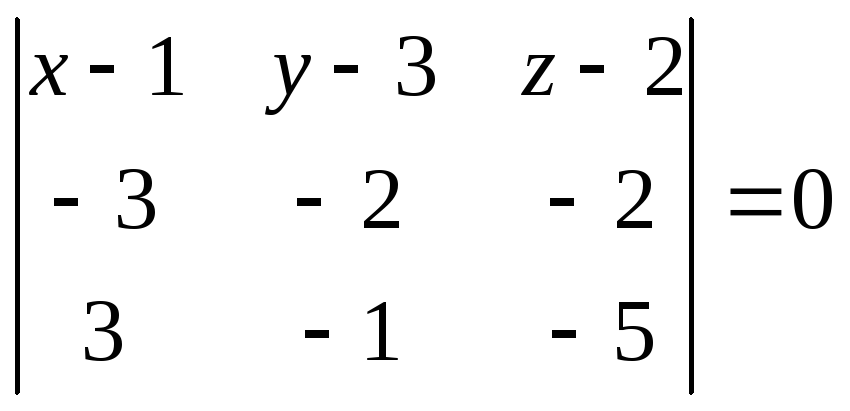

Запишем полученное уравнение в общем виде, т.е. в виде . Для этого раскроем определитель по первой строке. После преобразований получим:.

2) Найти нормальный вектор плоскости .

Решение.

Нормальный вектор - это вектор, перпендикулярный плоскости. Если плоскость задана общим уравнением, то нормальный вектор имеет координаты.

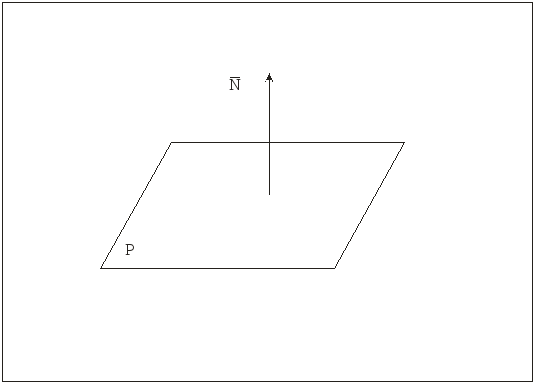
Рис. 3

Для плоскости нормальным является вектор=.

Отметим, что любой вектор, коллинеарный вектору =так же является нормальным вектором плоскости. Таким образом, при каждом ненулевомвектор с координатамибудет являться нормальным вектором рассматриваемой плоскости.

3) Найти косинус угла между плоскостями и.

Решение.

Угол между двумя плоскостямиипредставляет собой угол между их нормальными векторами и определяется равенством

Для плоскости координаты нормального вектораопределяются равенствами,,. Для плоскости- равенствами,,. Следовательно, =.

4) Составить уравнение плоскости , проходящей через точкупараллельно плоскости:.

Решение.

Уравнение плоскости, проходящей через точку , имеет вид

(3.8)

Подставим в уравнение (3.8) координаты точки :.

Условие параллельности плоскостей иимеет вид

(3.9)

Так как плоскости ипараллельны, то в качестве нормального вектораплоскостиможно взять нормальный векторплоскости, т.е. в формуле (3.9) отношениеможно принять равным единице. Следовательно, уравнение плоскостипримет вид. Запишем это уравнение в общем виде:.

5) Найти расстояние от точки до плоскости:.

Решение.

Расстояние от точкидо плоскостипредставляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой

(3.10)

Для плоскости координаты нормального вектораопределяются равенствами,,. Следовательно,.

6) Составить канонические уравнения прямой, проходящей через точки и.

Решение.

Уравнения прямой, проходящей через точки иимеют вид

(3.11)

Так как ,, то в силу (3.11) получим уравненияили.

7) Найти направляющий вектор прямой .

Решение.

Направляющий вектор - это вектор, параллельный прямой.

Если прямая задана каноническими уравнениями , то направляющий векторимеет координаты.

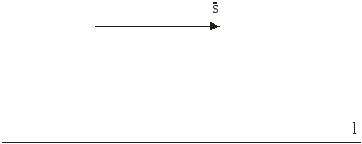
Рис. 4

Для рассматриваемой прямой направляющим вектором является вектор.

Отметим, что любой вектор, коллинеарный вектору так же является направляющим вектором прямой. Таким образом, при каждом ненулевомвектор с координатамибудет являться направляющим вектором рассматриваемой прямой.

8) Найти косинус угла между прямыми и.

Решение.

Угол между двумя прямымиипредставляет собой угол между их направляющими векторами и определяется равенством

Для прямой координаты направляющего вектораопределяются равенствами,,. Для прямой- равенствами,,. Значит,.

9) Составить канонические уравнения прямой , проходящей через точкупараллельно прямой:.

Решение.

Канонические уравнения прямой имеют вид . Здесь- координаты точки, через которую проходит прямая.

В канонические уравнения прямой подставим координаты точки. Получим:.

Условие параллельности прямых иимеет вид

(3.12)

Так как прямые ипараллельны, то в качестве направляющего векторапрямойможно взять направляющий векторпрямой, т.е. в формуле (3.12) отношениеможно принять равным единице. Следовательно, уравнение прямойпримет вид.

10) Найти угол между прямой :и плоскостью:.

Решение.

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Угол между прямой и плоскостью равен, где- угол между направляющим векторомпрямой и нормальным векторомплоскости.

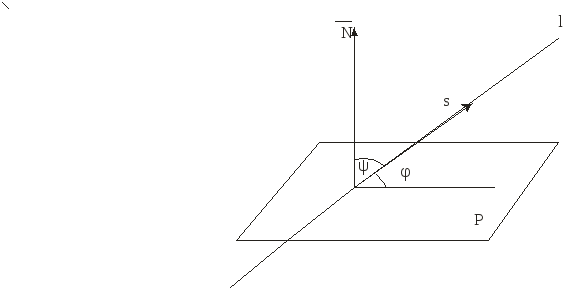
Рис. 5

Угол между прямойи плоскостьюопределяется формулой

Для плоскости :координаты нормального вектораопределяются равенствами,,. Для прямой:координаты направляющего вектора- равенствами,,. Синус угла между прямой и плоскостью равен=. Следовательно,.

11) Составить уравнение плоскости , проходящей через точкуперпендикулярно прямой:.

Решение.

Уравнение плоскости, проходящей через данную точку, имеет вид .

Подставим в указанное уравнение координаты точки . Получим:.

Условие перпендикулярности плоскости и прямойимеет вид

(3.13)

Так как искомая плоскость перпендикулярна прямой, то в качестве нормального вектораплоскости можно взять направляющий векторпрямой, т.е. в формуле (3.13) отношениеможно принять равным единице. Следовательно, уравнение плоскостипримет вид. Запишем это уравнение в общем виде:.

12) Составить канонические уравнения прямой , проходящей через точкуперпендикулярно плоскости:.

Решение.

Канонические уравнения прямой, проходящей через данную точку, имеют вид .

Подставим в эти уравнения координаты точки . Получим:

Условие перпендикулярности прямой и плоскостиимеет вид.

Так как прямая перпендикулярна плоскости, то в качестве направляющего векторапрямойможно взять нормальный векторплоскости, т.е. в формуле (3.13) отношениеможно принять равным единице. Следовательно, уравнение прямойпримет вид:.

13) Найти координаты точки пересечения прямой :и плоскости:.

Решение.

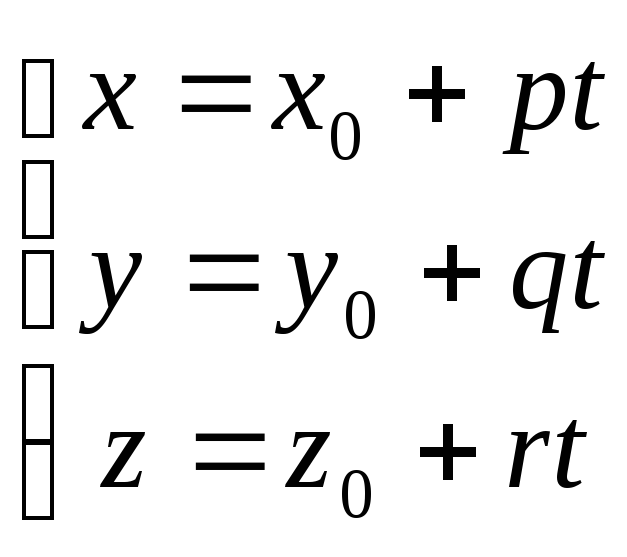Координаты точки пересечения прямойи плоскостипредставляют собой решение системы

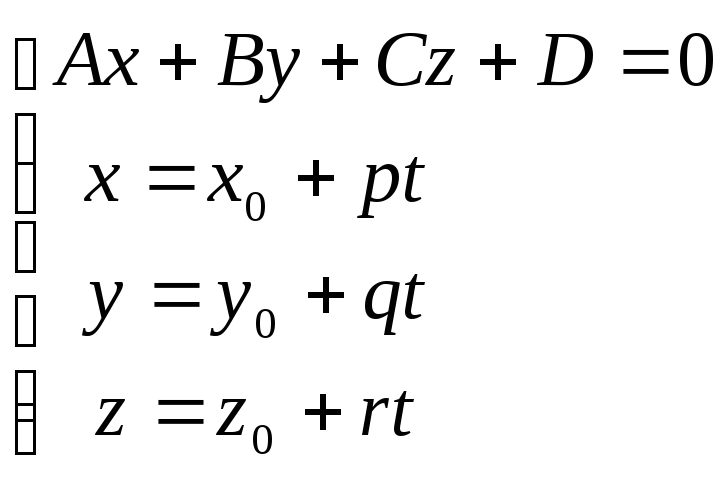(3.14)

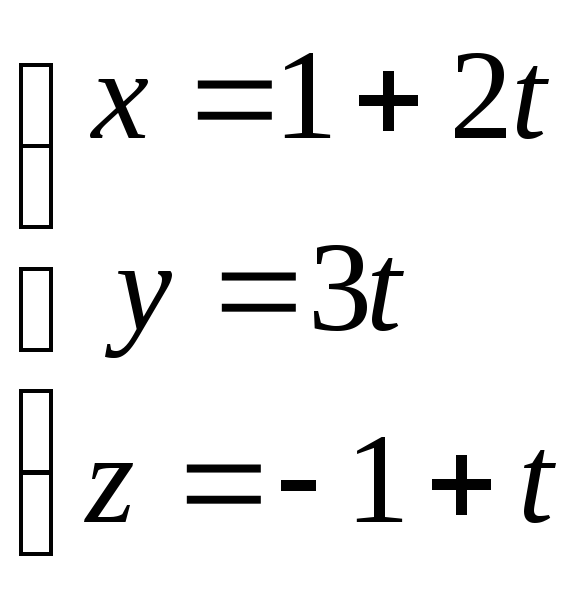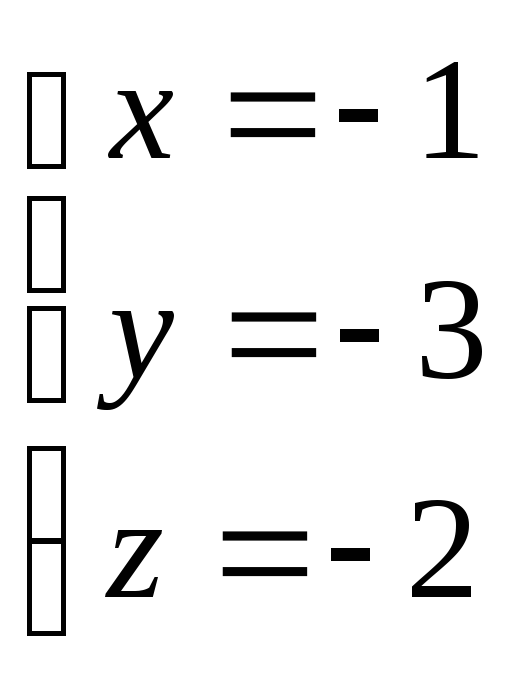Запишем параметрические уравнения прямой :и подставим выражения дляв уравнение плоскости:. Отсюда;. Подставим найденное значениев параметрические уравнения прямой:. Следовательно,.