
Кафедра информатики
Сборник лабораторных работ по курсу «Алгоритмизация и программирование».
Лабораторная работа № 4.
Программирование
вложенных циклических процессов
Цель работы.
Приобретение навыков построения алгоритмов и программ со структурой вложенных циклов, отработка характерных приемов программирования при вычислении суммы и произведения величин.
Краткая теория.
Наиболее часто в практике программирования встречаются алгоритмы циклической структуры, когда одну и ту же последовательность действий необходимо выполнить многократно при различных значениях входящих в них величин. К алгоритмам такого типа относятся задачи вычисления суммы или произведения значений некоторой функции y = f(x) при различных значениях аргумента x:
![]()
![]() ,
,
где
значения![]() могут являться элементами заданного
массива
могут являться элементами заданного
массива
![]() ,
вычисляться по рекуррентным соотношениям
,
вычисляться по рекуррентным соотношениям
![]() и т.п. Это означает, что необходимо
организовать циклический вычислительный
процесс, в котором происходит не только
вычисление значений заданной функции
y=f(x)
при каждом новом значении аргумента,
но и одновременное накопление сумм
(произведений) путем прибавления
(умножения) полученного значения к сумме
(произведению) всех предыдущих.
и т.п. Это означает, что необходимо
организовать циклический вычислительный
процесс, в котором происходит не только
вычисление значений заданной функции
y=f(x)
при каждом новом значении аргумента,
но и одновременное накопление сумм
(произведений) путем прибавления
(умножения) полученного значения к сумме
(произведению) всех предыдущих.
На
рис. 7 представлена блок-схема вычисления
![]() где
где
![]() - элементы массива
- элементы массива
![]() .
.
Общая
формула, используемая для накопления
суммы может быть представлена в виде:
![]() .
.
Отметим,
что в этой формуле знак «=» играет не
свою необычную роль знака равенства, а
роль знака присваивания: переменной S
присваивается новое значение, которое
на величину
![]() больше прежнего значения S.
больше прежнего значения S.
Если
начальное значение переменой S
предварительно (до входа в цикл) задать
равным нулю (S
= 0), то после первого выполнения цикла
значение S
будет равно первому значению функции
![]() и при каждом новом происхождении цикла
значение увеличивается на очередной
член суммы:
и при каждом новом происхождении цикла
значение увеличивается на очередной
член суммы:
![]() и т.д.
и т.д.

Рис. 7. Блок-схема алгоритма вычисления сумму элементов массива.
Аналогичным
образом организуется циклический
алгоритм накопления произведения
![]() .
Разница состоит в том, что начальное
значение P
должно быть равно единице (P
= 1), а формула накопления имеет вид:
.
Разница состоит в том, что начальное
значение P
должно быть равно единице (P
= 1), а формула накопления имеет вид:
![]() .
.
Содержание задания.
Составить алгоритм и написать программу для вычисления предложенных выражений, используя структуру вложенных циклов. Для каждого значения параметра внешнего цикла выводится значение внешней скобки.
Варианты задания.
-
Вычислить значение выражения

где z = 1.05
-
Вычислить значение выражения

где x = 1.55; y = -2.25
-
Вычислить значение выражения

где x = 2.43
-
Вычислить значение выражения

где x = 1.72; y = 2.45
-
Вычислить значение выражения

где y = 2.25
-
Вычислить значение выражения:

где z = 1.873
-
Вычислить значение выражения

где z = 1.33
-
Вычислить значение выражения

где x = 1.12; y = 2.24
-
Вычислить значение выражения
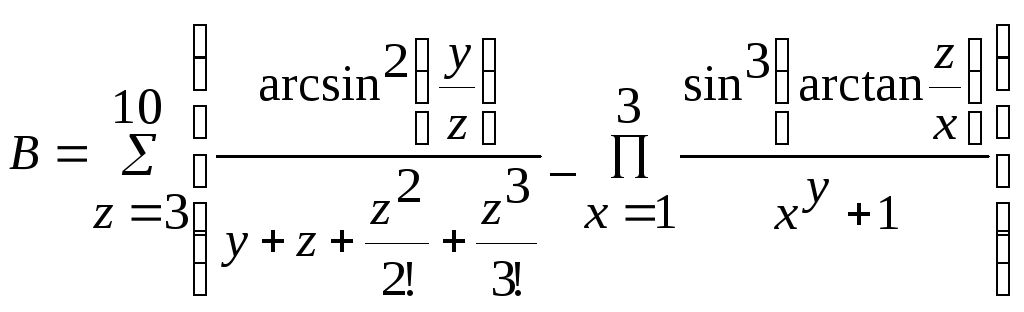
где y = 2.15
-
Вычислить значение выражения

где x = 1.19; y = 0.02
-
Вычислить значение выражения

где z = 1.32
-
Вычислить значение выражения
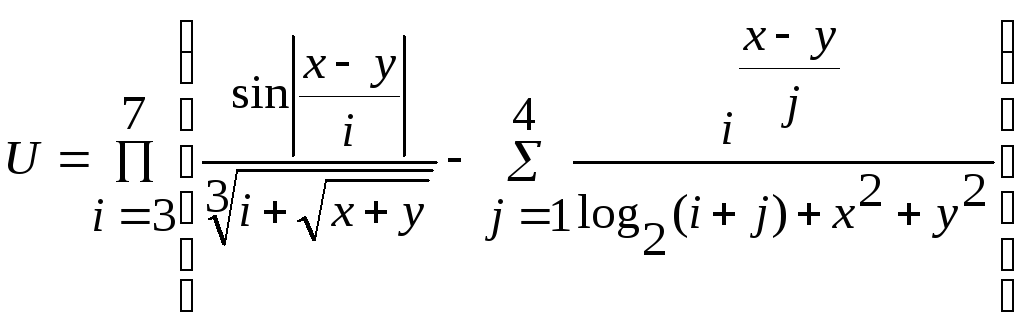
где x = 3.42; y = 2.9
-
Вычислить значение выражения

где x = 3.140
-
Вычислить значение выражения

где z = 0.92
-
Вычислить значение выражения

где x = 2.21; y = 0.72
-
Вычислить значение выражения

где z = 1.341; x = -0.675
-
Вычислить значение выражения
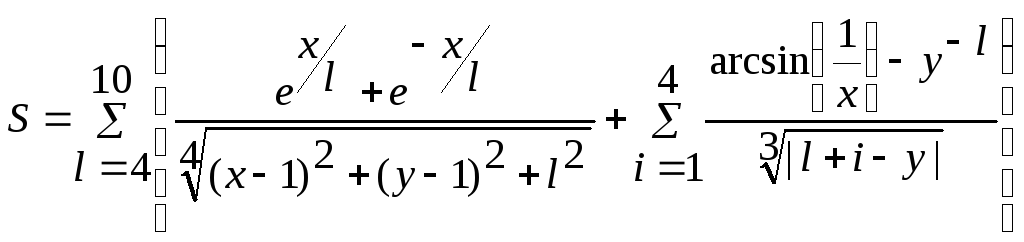
где x = 3.45; y = 2.9
-
Вычислить значение выражения

где y = 1.1
-
Вычислить значение выражения

где x = 0.981; y = 0.12; z = 3.65
-
Вычислить значение выражения

где x = 0.95
-
Вычислить значение выражения

где x = 0.86
-
Вычислить значение выражения

где z = 1.1; y = 1.1
-
Вычислить значение выражения

где y = 0.72
-
Вычислить значение выражения
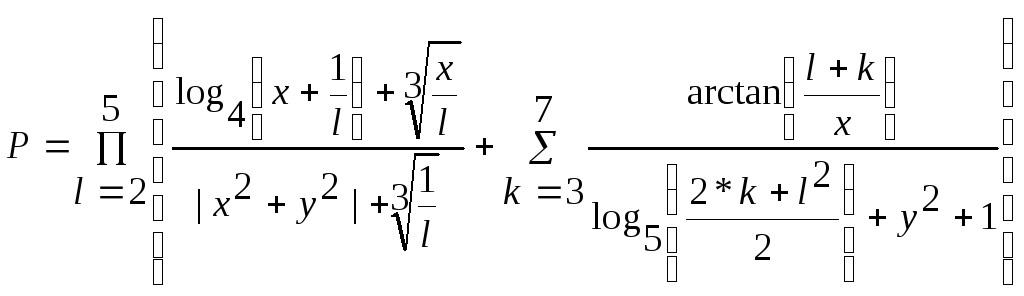
где x = 1.5; y = 0.94
-
Вычислить значение выражения

где y = 0.74
-
Вычислить значение выражения

где x = 3.21; y = 2.15
-
Вычислить значение выражения

где y = 0.34
-
Вычислить значение выражения

где x = 0.31; z = 5.8
-
Вычислить значение выражения

где z = 0.12
-
Вычислить значение выражения где x = 0.115; z = 1.092

