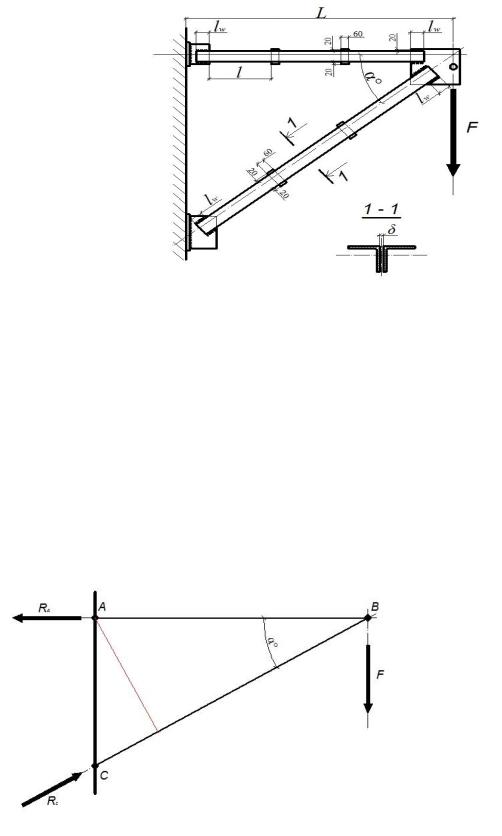
Пример решения задачи 3

Рис.1 Конструкция консоли

Исходные данные

L = 4,5м; α = 35°; F = 120 кН;

Сталь C245, Ry = 240Н/мм2 = 24кН/см2 (таб.В.5; СП 53-102-2004)

1. Подбор сечения

1.1 Определяем опорные реакции Узловые соединения считаем как шарнирные. Реакции вычисляем из уравнений моментов относительно точек «А» и «С»

Рис.2 Расчётная схема консоли

ΣМА = 0; F×L ̶ RC×L×sinα° = 0; RC = F / sinα° = 120 / sin35° = 209,2 кН

ΣМс = 0; F×L ̶ RА× L×tgα° = 0; RА = F / tgα° = 120 / tg35° = 171,4 кН

1.2 Усилия в стержнях АВ и ВС вычислим через проекции действующих сил на оси «X» и «Y»

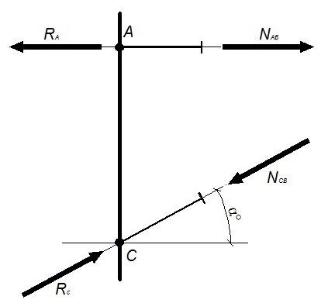
Рис.3 Схема к определению внутренних усилий (часть консоли заменена усилиями в стержнях для уравновешивания опорных реакций)

ΣY = 0; RC ×sinα° ̶ NCB×sinα° = 0; NCB = RC = 209,2кН;

ΣX = 0; NAB ̶ RA + RC ×cosα° ̶ NCB×cosα° = 0;

NAB = RA = 171,4 кН.

По направлению действия сил в данной конструкции, а также по результатам расчётов, видим, что стержень «АВ» работает на растяжение, а

стержень «ВС» - на сжатие.

Здесь:

N = NAB = 171,4 кН

A – площадь поперечного сечения двухветвевого стержня АВ (сеч. 1-1, рис.1)

Ry = 24 кН/см2 – расчётное сопротивление стали C245;

γc = 1 – коэф. условий работы стержня

Для вычисления требуемой площади принимаем

σ = Ry = 24 кН/см2

тогда

ААВ = NAB / Ryγc = 171,4 / 24 = 7,14(см2).

Площадь сечения одного уголка составит А1/2 = ААВ/2 = 7,14 / 2 = 3,57см2

Минимальный равнополочный уголок, рекомендуемый для применения

в строительстве – уголок № 5, с размерами полки 5,0×0,5см и площадью сечения 4,8 см2.

Вэтой связи, для стержня «АВ» принимаем два уголка №5.

1.4Подбор сечения сжатого стержня

N = NСB = 209,2 кН

A – площадь поперечного сечения двухветвевого стержня СВ (сеч. 1-1, рис.1)

Ry = 24 кН/см2 – расчётное сопротивление стали

γc = 1 – коэф. условий работы стержня

φ – коэф. устойчивости сжатого стержня. При расчёте сжатых стержней определение значения этого коэффициента является достаточно важной и ответственной задачей.