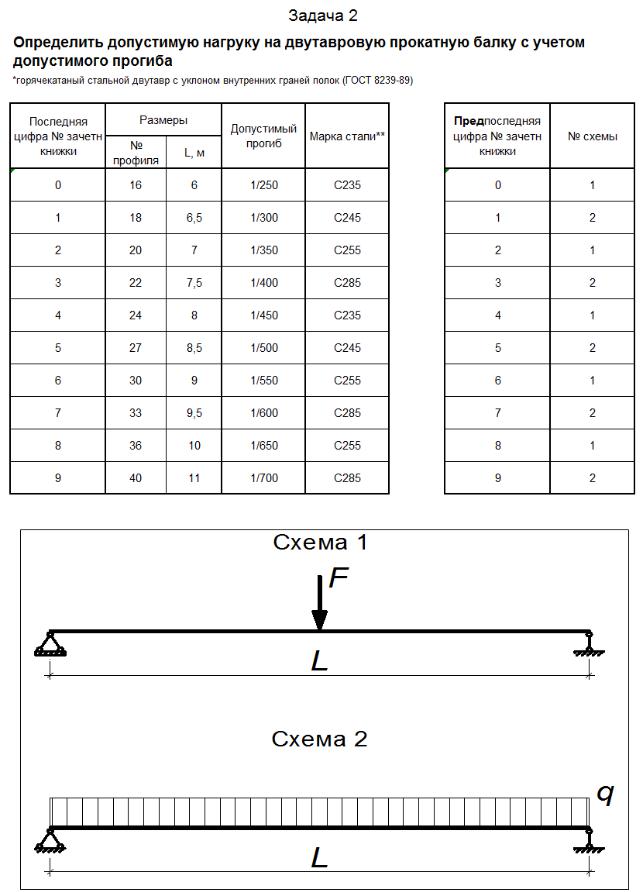
Задача 2
Пример решения задачи 2
Определить допустимую нагрузку на двутавровую прокатную балку с учётом допустимого прогиба
Исходные данные: |
|
№ профиля |
– 12; |
Пролёт L |
- 6м; |
Допустимый прогиб – 1/400;
Марка стали |
- С255. |
Т.к., геометрические характеристики проката приведены в ГОСТах в см, целесообразно в формулы подставлять величины, выраженные в сантиметрах или соотнесённые с сантиметрами. Например см2, кН/см2 и т.п.
Проверку несущей способности балки следует выполнить по нормальным напряжениям
σ = |
М |
≤ Ryγc |
(1) |
|
|
||||
|
|
|
||
|
|
|
|
Для схемы 1:
Мmax = |
|
(1.2) |
|
4 |
|||
|
|
Из (1)
Мmax = σ · Wx ,
при этом следует принять
σ = Ryγc
где
Ry = 240Н/мм2 = 240МПа = 24кН/см2 (СП 53-102-2004, табл. В.5);
γс = 1.0 – коэф. условий работы (СП 53-102-2004, табл.1, прим.5)
Wx = 58.4см3 (по ГОСТ 8239-89)
Тогда
Мmax = =1401,6кН·см
Из (2)
F = |
4 |
= |
4 · 1401,6 |
= 9,34кН |
|
|
|||
|
600 |
где
F – искомая нагрузка, кН;
L = 6м = 600см – пролёт между опорами по заданию;
Нагрузку, с учётом допустимого прогиба определим из формулы
f = |
3 |
|
|
(1.3) |
|
|
||
48 |
||
где Е = 20600кН/см2 – модуль упругости стали, не зависит от марки стали;
I = Ix = 350см4 – момент инерции для двутавра №12 (по ГОСТ 8239-89); f = [f ] – допустимое значение прогиба в см:
[ ] = 1/400 = 0.0025,
откуда
[f ] = 0.0025l = 0.0025×600(см) = 1.5(см)
Преобразовав формулу (1.3) с учётом поставленной задачи, получим
48 [ ] |
(1.4) |
F = |
3 |
|
откуда
F = 48 × 20600(кН/см2) × 350(см4) × 1.5(см) / 6003(см) = 2.4кН
Проверку несущей способности балки следует выполнить по нормальным напряжениям
|
|
|
|
|
(1) |
σ = |
|
≤ Ryγc |
|||
|
|
||||
Мmax = = |
|
(1.2) |
|||
4 |
|
|
|||
Здесь
Мmax = Fl / 4 = 2.4(кН) × 600(см) / 4 = 360 (кН×см); Wx = 58.4см3 (по ГОСТ 8239-89);
Ry = 240Н/мм2 = 240МПа = 24кН/см2 (СП 53-102-2004, табл. В.5); γс = 1.0 – коэф. условий работы (СП 53-102-2004, табл.1, прим.5).
Сучётом перечисленного
σ= 360 (кН×см) / 58.4(см3) = 6.16 кН/см2 << 24кН/см2
Как видно из расчётов, получаем почти четырёхкратный запас по прочности при ограничении по допустимому прогибу.
Для схемы 2:
Мmax = |
2 |
||
|
(2.1) |
||
8 |
|||
|
|
||
Для решения используем все приведённые ранее значения. Преобразовав формулу (2.1) в соответствии с поставленной задачей, получим
q = |
8 |
(2.2) |
|
2 |
|||
|
|
При этом из (1)
Мmax = σ · Wx ,
где
σ = Ryγc;
Ry = 240Н/мм2 = 240МПа = 24кН/см2 (СП 53-102-2004, табл. В.5);
γс = 1.0 – коэф. условий работы (СП 53-102-2004, табл.1, прим.5)
Wx = 58.4см3 (по ГОСТ 8239-89)
Тогда
Мmax = 24(кН/см2) × 58,4(см3) =1401,6кН·см,
q = 8× 1401,6(кН·см) / 6002(см) = 0,031кН/см
Нагрузку, с учётом допустимого прогиба определим из формулы
f = 54 (2.3)
384
где Е = 20600кН/см2 – модуль упругости стали, не зависит от марки стали;
I = Ix = 350см4 – момент инерции для двутавра №12 (по ГОСТ 8239-89); f = [f ] – допустимое значение прогиба в см:
[ ] = 1/400 = 0.0025,
откуда
[f ] = 0.0025l = 0.0025×600(см) = 1.5(см)
Преобразовав соответствующим образом (2.3) получим:
q = |
384 [ ] |
(2.4) |
|
54 |
|||
|
|
q = (384×20600(кН/см2) ×350(см4)×1,5(см)) / (5×6004(см)) = 0,0064 кН/см Также выполним проверку несущей способности балки по нормальным
напряжениям по (1), с учетом (2.1)
Т.е.,
Мmax = 0,0064(кН/см) × 6002(см) / 8 = 288 (кН×см);
Прочие значения приведены в предыдущем примере.
С учётом сказанного:
σ = 288 (кН×см) / 58.4(см3) = 4.93 кН/см2 << 24кН/см2.
Как видно из расчётов, также получаем значительный запас прочности при ограничении по допустимому прогибу.