математика

Занятие 3

Некоторые приложения двойных интегралов

Площадь плоской фигуры, ограниченной областью D, выражается в прямоугольных координатах

Dmax di!0 i=1

площадь плоской фигуры.

Объем цилиндра, ограниченного сверху непрерывной поверхностью z = f(x; y), снизу плоскостью Oxy и с боков прямой цилин-

дрической поверхностью, вырезающей на плоскости Oxy область D, выражается интегралом

ZZ

V = f(x; y) dxdy:

D

Рассмотрим тело, ограниченное сверху поверхностью z = f(x; y), z > 0, снизу замкнутой областью D плоскости Oxy, с боков

цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 14).

21

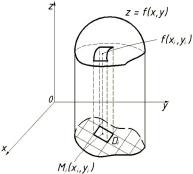
Ðèñ. 14.

Такое тело называется цилиндрическим. Найдем его объем V . Для этого разобьем область D (проекция поверхности z = f(x; y) на плоскость Oxy) произвольным образом на n областей Di, площа- ди которых равны Si (i = 1; : : : ; n). Рассмотрим цилиндрические столбики с основаниями Di, ограниченные сверху кусками поверхности z = f(x; y) (на рис. 14 один из них выделен). В своей совокупности они составляют тело V . Обозначив объем столбика с

произвольную точку

и заменим каждый столбик прямым цилиндром с тем же основанием Di и высотой zi = f(xi; yi). Объем этого цилиндра приближенно равен объему Vi цилиндрического столбика, т. е. Vi f(xi; yi) Si. Тогда получаем

nn

XX

Это равенство тем точнее, чем больше число n и чем меньше разме- ры областей Di. Естественно принять предел суммы (8) при условии, что число площадок Di неограниченно увеличивается (n ! 1), а каждая площадка стягивается в точку (max di ! 0), за объем V цилиндрического тела, т. е.

22

или, согласно равенству (2),

ZZ

V = f(x; y) dxdy: (9)

D

Èòàê, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела . В этом состоит геометри- ческий смысл двойного интеграла.

Если пластина занимает область D плоскости Oxy и имеет переменную плотность = (x; y), то масса m пластины выражается двойным интегралом

ZZ

m = (x; y) dxdy:

D

Требуется найти массу m плоской пластины D, зная, что ее поверхностная плотность = (x; y) есть непрерывная функция координат точки (x; y). Разобьем пластину D на n элементарных ча- стей Di (i = 1; : : : ; n), площади которых обозначим через Si. Â каждой области Di возьмем произвольную точку Mi(xi; yi) и вы- числим плотность в ней: (xi; yi).

Если области Di достаточно малы, то плотность в каждой точке Mi(xi; yi) 2 Di мало отличается от значения (xi; yi). Считая приближенно плотность в каждой точке области Di постоянной, равной(xi; yi), можно найти ее массу mi: mi (xi; yi) Si. Òàê êàê ìàñ- са m всей пластины D равна m =

имеем приближенное равенство

Точное значение массы получим как предел суммы (10) при условии n ! 1 и max di ! 0:

или, согласно равенству (2),

23

Итак, двойной интеграл от функции (x; y) численно равен массе пластины, если подынтегральную функцию (x; y) считать плотностью этой пластины в точке (x; y). В этом состоит физический

смысл двойного интеграла.

Статические моменты фигуры D относительно осей Ox и Oy могут быть вычислены по формулам

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d от точки до оси, т. е. Ml = m d2. Моменты инерции плоской фигуры относительно осей Ox и Oy могут быть вычислены по формулам

Задача 1. Вычислить объем тела, ограниченного плоскостью z = 0 и параболоидом z = 3 x2 y2.

Решение: Сверху данное тело ограничено параболоидом z = 3 x2 y2, поэтому V = RR 3 x2 y2 dxdy.

D

Ðèñ. 15.

24

Задача 2. Вычислить площадь плоской фигуры, ограниченной линиями y2 = x + 1 è x + y = 1.

Решение: Область D ограничена слева параболой y2 = x+1, справа прямой y = x + 1.

Ðèñ. 16.

Решая совместно два уравнения, находим точки их пересечения (0; 1) и (3; 2). Значит искомая площадь

Задача 3. Найти массу, статические моменты Sx è Sy è êîîð-

динаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом x2=4 + y2 = 1 и координатными осями. Поверх-

ностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

25

Решение:

Ðèñ. 17.

По условию поверхностная плотность пластины = kxy, где k коэффициент пропорциональности. По формуле

26

Задачи.

1.Найти объем тела, ограниченного z = 0, z = 2 y и цилиндром y = x2.

2. Найти объем тела, ограниченного поверхностями z = 4 y2, y = 0; 5x2, z = 0.

3.Найти объем тела, ограниченного поверхностями x2 +y2 = 2x, z = 2x, z = 4x.

4.Вычислить площадь и координаты центра масс плоской фигуры, ограниченной прямой y = 2 и y = x2 1.

5.Вычислить площадь и координаты центра масс плоской фи-

гуры, ограниченной синусоидой y = sin x, осью Ox и прямой

x = =4.

6.Вычислить площадь кругового сектора, соответствующего центральному углу (радиус круга равен 1).

7.Найти массу квадратной пластины D 0 6 x 6 2, 0 6 y 6 2, поверхностная плотность которой равна = x + y.

8.Найти массу пластины D, ограниченной прямыми x = 0, y = 0, x = 1, y = 1, с поверхностной плотностью = xy.

9.Найти массу пластины, ограниченной кривыми y = x2, y = p

x, если ее плотность равна (x; y) = x + 2y.

Контрольная работа по темеДвойной интеграл

1. Изменить порядок интегрирования в повторном интеграле

26 x

ZZ

02x

27

Решение: Область D не является правильной в направлении Ox. Представим ее в виде объединения правильных D1 è D2.

Ðèñ. 18.

Тогда

2. Перейдя к полярным координатам, вычислить площадь фи-

Ðèñ. 19.

Их уравнения в полярных координатах ' = 0, r = sin ' и

28

' = =6. Площадь фигуры вычисляется по формуле

3. Вычислить RR x2 + y dxdy, где D область, ограниченная

D

параболами y = x2, x = y2.

Решение:

Ðèñ. 20.

Область D является правильной, выберем направление Oy. Тогда

29

Криволинейные интегралы

Занятие 4

Криволинейный интеграл I рода. Основные понятия

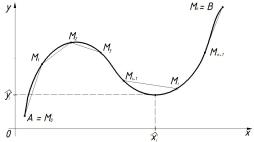
Пусть на плоскости Oxy задана непрерывная кривая AB (или L) длины l. Рассмотрим непрерывную функцию f(x; y), определенную в точках дуги AB. Разобьем кривую AB точками M0 = A; M1; : : :, Mn = B на n произвольных дуг Mi 1Mi с длинами li (i = 1; : : : ; n).

Ðèñ. 21.

Выберем на каждой дуге Mi 1Mi произвольную точку (^xi; y^i) è ñî-

Ее называют интегральной суммой для функции f(x; y) по кривой AB.

30