
Методичка_погрешности
.pdf
11
Точечная оценка – статистическая оценка, выраженная единственным числом.
Интервальная оценка – статистическая оценка представляемая интервалом значений, внутри которого с заданной вероятностью находится истинное значение оцениваемого параметра.
Точечные оценки погрешности измерений.
В соответствии с теорией вероятности и математической статистикой за истинное значение случайной величины а принимается ее среднее значение <a> .е. значение величины а, усредненное по всем возможным ее состояниям и с учетом вероятности появления каждого из состояний (т.е. по генеральной совокупности).
Точечными оценками погрешности измерения случайной величины являются ее среднеарифметическое значение, среднеквадратическое значение отклонения отдельного измерения и среднеквадратическое отклонение среднеарифметического, удовлетворяющие требования несмещенности, состоятельности и эффективности.
Точечной оценкой истинного значения физической величины является ее среднеарифметическое значение, полученное в результате многократно проведенных измерений и принимаемое за действительное значение
|
a1 a2 aN |
|
1 |
N |
|
|
A |
|
ai |
(5) |
|||
|
|
|||||
|
N |
N i 1 |
|
|||
где А – среднеарифметическое значение многократных измерений, ai - результат i-го отдельного измерения, N – число измерений.
За действительное значение физической величины принимается ее среднеарифметическое значение – наиболее достоверное значение, которое можно приписать измеряемой величине на основании многократных измерений.
Отклонение среднеарифметического значения А от истинного значения величины а характеризуется понятием дисперсии.
Дисперсией среднеарифметического D(A) называется откло-
нение среднеарифметического значения физической величины от ее среднего, т.е. истинного, значения:

12
|
|
|
1 |
N |
|
2 |
1 |
N |
|
|
1 |
|
2 |
||
|
|
|
|
|
|||||||||||
D( A) ( A a 2 |
|
ai |
a |
|
|
|
(ai a )2 |
|
|
N 2 |
|
||||
|
N |
2 |
N |
2 |
N |
||||||||||
|
|
|
N i 1 |
|
|
|
i 1 |
|
|
||||||
(6)
где: <a> - среднее значение измеряемой величины, равное истинному значению, - среднеквадратическая погрешность однократного измерения.
Из выражения для дисперсии среднеарифметического (6) следует,
при бесконечном увеличении числа измерений, N , дисперсия среднеарифметического D(A) стремится к нулю, D(A) 0 и, следовательно, среднеарифметическое значение измеряемой величины A будет стремится к ее истинному значению <a>.
среднеквадратическое отклонение случайной погрешности результата
многократного измерения в 
 N раз меньше среднеквадратичного отклонения результата однократного измерения .
N раз меньше среднеквадратичного отклонения результата однократного измерения .
Зная среднее арифметическое значение, можно определить отклонение результата единичного измерения от среднего значения, т.е. его погрешность:
i аi А |
…7 |
Тогда сумма отклонения результата измерений от среднего значения будет равна нулю, а сумма их квадратов минимальна. Эти свойства лежат в основе обработки результатов измерений, контроля правильности вычислений, регрессионного анализа.
Точно так же, как невозможно опытным путем определить среднее значение величины, нельзя определить и среднеквадратическое значение отклонения отдельного измерения . При конечном числе измерений N, возможно лишь найти его оценку, которая равна:
|
1 |
|
N |
|
|
0 |
|
(ai a ) 2 |
…8 |
||
N 1 |
|||||
|
i 1 |
|
|||
|
|
|
|
||
Для многократного измерения оценка среднеквадратического отклонения среднеарифметического (среднеквадратическая погрешность результата многократных измерений) равна:
|
|
1 |
|
N |
|
A |
|
|
( ai A )2 |
…9 |
|
|
|
||||
N( N |
|
||||
|
|
1) i 1 |
|
||

13
При увеличении количества измерений, N среднеарифметическое значение А стремится к среднему значению , а среднеквадратическая погрешность становится пренебрежимо малой А 0.
Интервальная оценка.
Интервальная оценка погрешности состоит в указании доверительного интервала, в котором измеряемая величина находится с известной вероятностью. Т.е. определяется вероятность появления погрешности , величина которой не выходит за некоторые заданные границы (интервал). За середину этого интервала принимается среднеарифметическое значение величины, а сам интервал называют доверительным интервалом.
Интервальная оценка погрешности основывается на понятии «функция распределения вероятности погрешности», которая определяет вероятность возникновения данной величины случайной погрешности. На практике обычно рассматривают некоторое, наиболее простое для анализа и расчетов, приближение к реальному закону распределения,. В случае технических измерений в качестве такого приближения (аппроксимации) наиболее часто используют закон нормального распределения. Рассматриваются также законы равномерного распределения и треугольный закон распределения, распространенный среди цифровых приборов.
Свойства нормального распределения.
Нормальное распределение есть распределение вероятности суммы независимых случайных величин с конечными дисперсиями при неограниченном увеличении числа слагаемых.
Сточки зрения процесса измерений нормальное распределение погрешностей есть результат одновременном действия большого числа независимых
факторов, каждый из которых незначительно и независимо от других оказ ы- вает в влияние на суммарную погрешность измерений. Именно по этому случайная погрешность измерений наиболее часто описываются законом нормального распределения поскольку
В реальности мы всегда имеем дело с ограниченным числом источников погрешностей. Однако, при сложении даже только четырех-пяти случайных величин с различными законами распределения, но с соизмеримыми дисперсиями (т.е. со сравнимыми величинами погрешностей), мы приходим к закону распределения погрешностей, близкому к нормальному. Особенно, если плотность вероятности достаточно велика
14
P( ) |
|
|
|
|
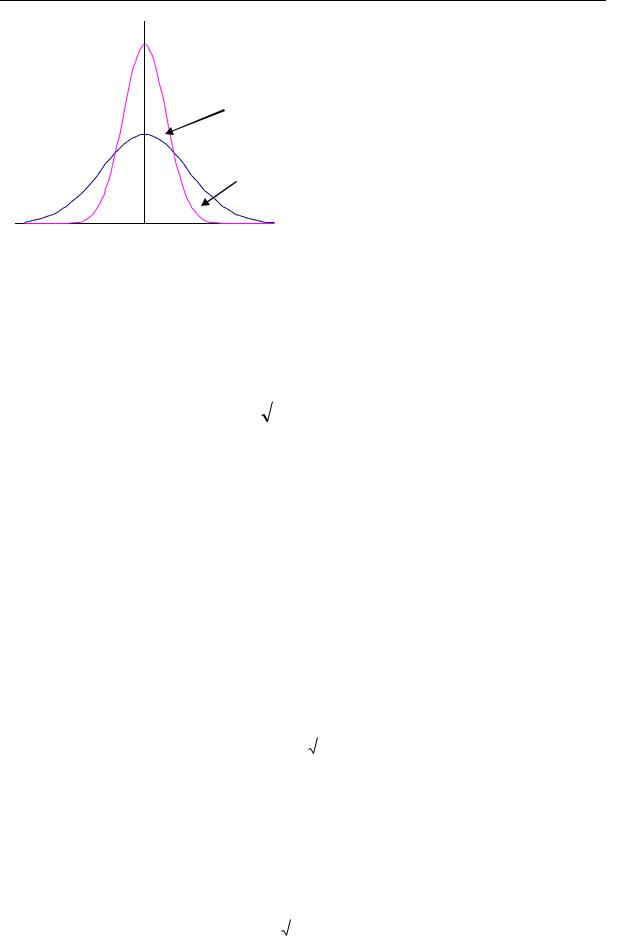
Рис. 3.. График нормального (Гауссова) рас- |
|
1 |
пределения вероятности случайной погрешно- |
|
сти P( ) при двух значениях среднеквадратич- |
|
2=2 1 |
|
|
|
ной погрешности 1 и 2 ( 2=2 1) |
|
|
|
2 |
0 |
|
|
Функция распределения вероятности p( ) определяет вероятность того, что величина случайной погрешности окажется равной заданной. Нормальное распределение плотности вероятности p( ) центрированной случайной погрешности описывается функцией Гаусса:
|
|
1 |
|
|
|
2 |
|
|
|
|
p( ) |
|
|
|
|
|
|
|
|
|
…10 |
|
|
|
|
|
2 |
|||||
|
|
2 |
|
exp |
2 |
|
||||
|
|
|
|
|
|
|
|
|||
где: - величина случайной погрешности, |
- среднеквадратическое откло- |
|||||||||
нение измеряемой величины от истинной. Из выражения (10) следует:
1). Площадь, ограниченная графиком и осью абсцисс, всегда остается неизменной и равной 1 при любых значениях , что соответствует тому, что вероятность появления ошибки, отличной от нуля равна р( 0)=1:
|
|
p( )d 1 |
…11 |
2). Вероятность того, что величина случайной погрешности окажется в интервале от =- до =+а, определяется соотношением:
|
|
1 |
|
a |
2 |
|
|
|
|
P( ) |
|
|
|
|
exp( |
|
|
)d |
…12 |
|
|
|
|
2 |
2 |
||||
|
|
2 |
|||||||
|
|
|
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Можно выразить величину интервала в единицах , т.е. принять = t , где t – безразмерный коэффициент, и таким образом связать величину ожидаемой погрешности = со среднеквадратичным отклонением. Тогдао интеграл (12) преобразуется к следующему виду:
|
|
2 |
|
t |
u |
2 |
|
|
|
P( t t ) |
|
|
exp( |
|
)du 2 (t) |
(13) |
|||
|
|
|
|
|
|||||
2 |
2 |
||||||||
|
|
0 |
|
|
|||||

15
Этот интеграл определяет вероятность нахождения величины погрешности в интервале = t и называется интегралом ошибок. Значения интеграла ошибок Ф(t) заранее вычислены, затабулированы и широко используются в практических расчетах.
При нормальном законе распределения с помощью интеграла ошибок можно вычислить вероятность того, что величина случайной погрешности лежит в некотором заданном интервале значений.
В частности:
P(-3 < 3 )=2Ф(3)=0,9972 - случайная составляющая погрешности измерения с вероятностью 0,9972 не выходит за пределы интервала 3
P(-2,67 < <2,6 )=2Ф(2,6)=0,99 - случайная составляющая погрешности измерения с вероятностью 0,99 лежит в пределах 2,6
P(-2 < <2 )=2Ф(2)=0,95 - случайная составляющая погрешности измерения с вероятностью 0,95 лежит в пределах интервала 2 .
Р(-(- < < )=2Ф(1)=0,68 - вероятность того, что величина погрешности не превышает своего среднеквадратического значения составляет 0,68
Принято считать, что при достаточно большом числе отдельных измерений, N 30, то с высокой степенью точности среднеарифметическое значение измеряемой величины равно ее среднему, принимаемому за ее действительное значение. При этом среднеквадратическое отклонение отдельного измерения 0 равно среднеквадратическому отклонению многократного измерения А и соответствующему параметру закона нормального распределения .
A a ; |
A 0 |
Вероятная погрешность.
Величина вероятной погрешности определяет интервал значений случайной погрешности - доверительный интервал, которые эта погрешность может принимать с доверительной вероятностью равной 0,5 .
Вероятной погрешностью называют такую величину погрешности, относительно которой при повторных измерениях 50% случайных погрешностей будет по абсолютной величине больше вероятной погрешности, а другие 50% - меньше ее.
При нормальном законе распределения вероятная погрешность результата измерений, т.е. погрешность определения среднеарифметического значения, будет равна
|
|
|
16 |
||
|
|
|
|
|
|
A |
2 |
A |
(14) |
||
3 |
|||||
|
|
|
|
||
Правило 3
При N> 30 принято отбрасывать результаты отдельных измерений, отличающихся от среднеарифметического более, чем на 3 , для которых А-аi >3 , поскольку вероятность их появления составляет менее 0,003.
При нормальном законе распределения за максимальную величину случайной составляющей погрешности принимают ее значении, равное трем значениям среднеквадратичной погрешности
max=3 .
Погрешности более, чем второе превосходящие среднеквадратичное значение считаются грубыми и исключаются из дальнейшего рассмотрения.
Распределение Стьюдента.
На практике возможное количество измерений достаточно ограничено и для определения доверительного интервала вместо закона нормального распределения результата используют распределение Стьюдента. Смысл этого распределения заключается в коррекции нормального (гауссова) распределения при небольшом количестве измерений, когда значительные случайные погрешности могут вносить непропорционально большой вклад в итоговое распределение.
Распределению Стьюдента соответствует свой интеграл ошибок, значения которого табулированы в виде коэффициентов Стьюдента tN, Эти коэффициенты зависят от задаваемой доверительной вероятности Р и количества измерений N (Таблица 1). Для определения доверительного интервала среднеквадратическая погрешность А умножается на коэффициент Стьюдента, взятый из соответствующей таблицы, и границы доверительного интервала записываются в виде:
A(Р, N) A tN A |
(15) |
Интервальная оценка и понятие доверительного интервала с точки зрения анализа данных и организации работы систем управления являются более информативными, чем точечные оценки. Если результат отдельного измерения выходит за пределы заранее определенных доверительных границ, то это есть нарушение статистической закономерности, свойственной данному объекту

17
Таблица 1. Коэффициенты Стьюдента
|
|
Коэффициенты Стьюдента |
|
|||
n |
|
|
Значения Р |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0.6 |
0.8 |
0.95 |
|
0.99 |
0.999 |
|
|
|
|||||
|
|
|
|
|
|
|
2 |
1.376 |
3.078 |
12.706 |
|
63.657 |
636.61 |
3 |
1.061 |
1.886 |
4.303 |
|
9.925 |
31.598 |
4 |
0.978 |
1.638 |
3.182 |
|
5.841 |
12.941 |
5 |
0.941 |
1.533 |
2.776 |
|
4.604 |
8.610 |
6 |
0.920 |
1.476 |
2.571 |
|
4.032 |
6.859 |
7 |
0.906 |
1.440 |
2.447 |
|
3.707 |
5.959 |
8 |
0.896 |
1.415 |
2.365 |
|
3.499 |
5.405 |
9 |
0.889 |
1.397 |
2.306 |
|
3.355 |
5.041 |
10 |
0.883 |
1.383 |
2.262 |
|
3.250 |
4.781 |
11 |
0.879 |
1.372 |
2.228 |
|
3.169 |
4.587 |
12 |
0.876 |
1.363 |
2.201 |
|
3.106 |
4.437 |
13 |
0.873 |
1.356 |
2.179 |
|
3.055 |
4.318 |
14 |
0.870 |
1.350 |
2.160 |
|
3.012 |
4.221 |
15 |
0.868 |
1.345 |
2.145 |
|
2.977 |
4.140 |
16 |
0.866 |
1.341 |
2.131 |
|
2.947 |
4.073 |
17 |
0.865 |
1.337 |
2.120 |
|
2.921 |
4.015 |
18 |
0.863 |
1.333 |
2.110 |
|
2.898 |
3.965 |
19 |
0.862 |
1.330 |
2.101 |
|
2.878 |
3.922 |
20 |
0.861 |
1.328 |
2.093 |
|
2.861 |
3.883 |
21 |
0.860 |
1.325 |
2.086 |
|
2.845 |
3.850 |
22 |
0.859 |
1.323 |
2.080 |
|
2.831 |
3.819 |
23 |
0.858 |
1.321 |
2.074 |
|
2.819 |
3.792 |
24 |
0.858 |
1.319 |
2.069 |
|
2.807 |
3.767 |
25 |
0.857 |
1.318 |
2.064 |
|
2.797 |
3.745 |
26 |
0.856 |
1.316 |
2.060 |
|
2.787 |
3.725 |
27 |
0.856 |
1.315 |
2.056 |
|
2.779 |
3.707 |
28 |
0.855 |
1.314 |
2.052 |
|
2.771 |
3.690 |
29 |
0.855 |
1.313 |
2.048 |
|
2.763 |
3.674 |
30 |
0.854 |
1.311 |
2.045 |
|
2.756 |
3.659 |
31 |
0.854 |
1.310 |
2.042 |
|
2.750 |
3.646 |
40 |
0.851 |
1.303 |
2.021 |
|
2.704 |
3.551 |
60 |
0.848 |
1.296 |
2.000 |
|
2.660 |
3.460 |
12 |
0.845 |
1.289 |
1.980 |
|
2.617 |
3.373 |
0 |
|
|||||
|
|
|
|
|
|
|
∞ |
0.842 |
1.282 |
1.960 |
|
2.576 |
3.291 |
.
При измерения это свидетельствует о наличии в результатах грубой погрешности. Такие результаты должны быть выявлены и отброшены, а все расчеты проведены заново без учета отброшенных значений.

18
Пример:
С помощью стрелочного вольтметра измерялось напряжение в электрической сети. Измерения выполнялись 8 раз, их результаты приведены в таблице 1
№ пп. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
Измеренное |
226 |
228 |
214 |
216 |
239 |
227 |
223 |
219 |
|
значение, В |
|||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Погрешность |
|
|
|
|
|
|
|
|
|
отдельного из- |
+2 |
+4 |
-10 |
-8 |
+15 |
+3 |
-1 |
-5 |
|
мерения, В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднеарифметическое значение измеренного напряжения, которое мы принимаем за его действительное значение, равно 224 В. Тогда можно вы числить погрешности отдельных измерений и рассчитать среднеквадратическое отклонение:
|
|
|
U 2 |
U 2 |
... U 2 |
4 16 100 64 225 9 1 25 |
|
|
|
444 |
|
|
|
|
|
А |
|
1 |
2 |
8 |
|
|
|
|
|
2,816 |
В 3В |
||
|
|
|
|
|||||||||||
|
|
|
N( N 1) |
8 7 |
|
|
|
56 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
Определим интервал, в котором измеряемого напряжения находится с доверительной вероятностью 99%. Для этого по таблице коэффициентов распределения Стъюдента для доверительной вероятности Р=0,99 и N=8 находим tn = 3,5. Отсюда согласно формуле (1.11) находим величину напряжения: U=224 В ± 3 3,5
В= (224±10,5) В = (224±11) В. Здесь мы учли, что данные измерений известны с точностью 1 В, поэтому все вычисляемые значения также округляются до 1 В.
Полученная оценка показывает, что погрешность одного из измерений (№ 5) не укладывается в установленный доверительный интервал, т.е. содержит грубую погрешность. Это значение должно быть исключено, а процедура определения погрешности проведена заново, но при количестве измерений N=7. В результате мы получим, что с вероятностью 0,99 действительное значение напряжения лежит в пределах (221±8) В.
4.СИСТЕМАТИЧЕСКАЯ ПОГРЕШНОСТЬ.
Втехнических измерениях к систематическим погрешностям относят те погрешности, независимо от их природы и источника, величина которых
может быть определена или спрогнозирована еще до проведения измерений. Определение и исключение систематической погрешности является одной из главных задач на всех стадиях планирования и проведения измерений.
При проведении технических измерений возможны систематические погрешности, которые могут быть выявлены и учтены только при глубоком понимании сущности объекта измерений, методики и средств измерений. Особенно это свойственно измерениям, которые производятся на крупных тех-

19
нических агрегатах, в сложных технологических процессах, например, металлургических.
Применительно к задачам автоматизации выявление и оценка систематической погрешности означает, что расчет ожидаемой систематической погрешности измерений или контроля должен начинаться еще на этапе проектирования САУ. На этом этапе необходимо:
выбрать методы и средства измерений, адекватные поставленной задаче, определить и, при необходимости, подтвердить метрологические характеристики средств измерений:
выявить потенциальные источники погрешностей и принять меры по их устранению или минимизации воздействия на результат измерений,
провести оценку ожидаемой систематической погрешности.
Предварительная работа выполняется методами теоретического анализа, математического, имитационного и физического моделирования процесса измерений. Однако, все эти действия не позволяют абсолютно уверенно оценить и (или) исключить систематическую погрешность. Поэтому особое значение приобретает этап наладки средств автоматизации, включая средства и методы измерений, в ходе которого реальные значения и источники погрешностей выявляются экспериментально.
Для исключения и (или) оценки систематических погрешностей в процессе подготовки измерений применяются самые различные способы. В том числе:
Способ замещения - измеряемый объект заменяется известной мерой. Такой мерой может служить образцовый объект, имеющим туже природу, что и измеряемый, но характеристики которого заранее известны с высокой то ч- ностью.
Способ последовательных наблюдений - последовательные измерения через равные промежутки времени позволяют определить и учесть скорость изменения прогрессирующих систематических погрешностей
Метод рандомизации - искусственная трансформация систематической погрешности в случайную. Например, для измерения физической величины одновременно используются несколько разнотипных приборов с последующим усреднением их показаний; применяют наложение известных периодических возмущений (изменение методики и условий измерений, параметров внешней среды и т.п.), которые не влияют на измеряемую величину, но могут изменить систематическую погрешность ее измерения.
Повторные и многократные измерения при измененяемых внешних условиях, при других методиках и технических средствах измерений. Сопоставление результатов, полученных в различных условиях измерений, позво-

20
ляет минимизировать систематические ошибки, обусловленные неизвестными и (или) не формализуемыми причинами. В том числе:
особенностями эксплуатации оборудования,
влиянием окружающей среды;
влиянием различных процессов, которые протекают в объекте измерений, но прямо не влияют на измеряемую величину.
Врезультате выполнения всех этих действий часть источников систематической погрешности вообще может быть устранена. Оставшаяся часть си-
стематической погрешности должна быть выявлена, а ее величина должна учитываться в результатах измерений в виде поправок.
Поправкой называется величина, одноименная с измеряемой, добавление которой к результату измерений исключает систематическую погрешность.
Поправочный множитель (поправочный коэффициент) это число, на которое умножается результат измерений с целью исключения систематической погрешности.
Поправки и поправочные коэффициенты в виде графиков, таблиц или формул прилагаются к паспорту прибора, методике измерений, стандарту предприятия или другому документу, регламентирующую данную процедуру технических измерений.
Большинство поправок не может быть точно определено ни расчетным путем, ни экспериментально, т.е. тоже содержат погрешность.
Все методы определения систематической погрешности в свою очередь содержат погрешность. Поэтому поправки также содержат погрешность и в принципе не могут полностью компенсировать систематическую составляющую погрешности.
в результатах измерений всегда остается некоторая остаточная величина систематической погрешности, которая называется неисключенным остатком систематической погрешности или неисклю-
ченной систематической погрешностью (НСП).
Принято, что при небольшом числе источников погрешности (n 3) верхняя граница НСП результата измерений определяется по максимуму суммарной погрешности:
m |
|
i |
(16) |
i 1
