3.2. Расчеты по уравнениям изотермы, изобары и изохоры химической реакции

Изменение изобарного потенциала при протекании химичес­кой реакции в газовой фазе: aA + bB = gG + rR при Р, Т = const можно вычислить по уравнению изотермы Вант-Гоффа:

.

При V, T = const уравнение изотермы позволяет вычислить изменение изохорного потенциала:

По знакам ∆G и ∆F можно судить о возможности и направлении протекания данной реакции. Если ∆G_P, T < 0 или ∆F_V, T < 0, реакция может протекать самопроизвольно в прямом направлении.

Зависимость константы равновесия от температуры выражается уравнениями изобары и изохоры Вант-Гоффа:

или ;

или .

В небольших температурных интервалах можно принять, что ∆Н ≠ f(T), тогда в интегральной форме уравнение изобары имеет вид

Графически в координатах это уравнение изображается прямой линией, тангенс угла наклона которой равен

Постоянная интегрирования j определяется отрезком, отсекаемым прямой на оси ординат, или вычисляется по формуле

.

Интегрируя в пределах от Т₁ до Т₂, получаем

.

Это уравнение позволяет вычислять ∆Н в небольших интервалах температур, если известны значения констант равновесия при двух температурах. При более точном интегрировании следует учитывать, что ∆Н = f(T).

Пример 15

Степень диссоциации фосгена по реакции СОCl₂ = CO + Cl₂ при 873 К и 1,38 · 10⁵ Н/м² равна 0,9. Определить, в каком направлении будет протекать процесс при следующих заданных значениях парциальных давлений компонентов:

№ п/п	, Н/м2	, Н/м2	, Н/м2
1	1,013	1,013	1,013
2	1,048	2,026	3,039
3	1,048	3,039	3,039

Решение

Определяем константу равновесия реакции

СОCl₂ = CO + Cl₂:

n(1 - α) nα nα

Подставим в уравнение для K_Р :

Направление процесса определяем по ∆G из изотермы химической реакции. В первом случае

значит, процесс идет самопроизвольно в прямом направлении.

Во втором случае

значит, система находится в равновесии.

В третьем случае

значит, процесс идет самопроизвольно в обратном направлении.

Пример 16

Возможен ли термодинамический процесс получения анилина из хлорбензола по уравнению, если известны стандартные изменения изобарного потенциала веществ, входящих в данную реакцию: ,, ,.

Вычислить K_р реакции при 298 К.

Решение

1. ,

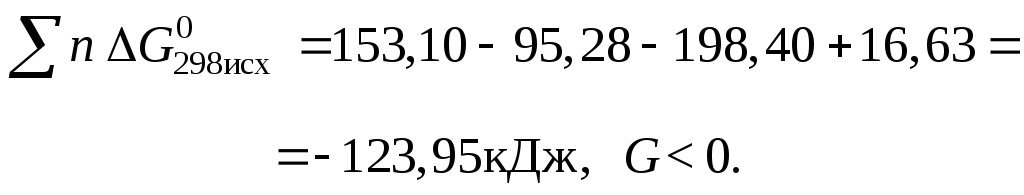
Следовательно, процесс возможен.

2. K_р вычисляется по уравнению изотермы для нормального сродства:

Пример 17

Рассчитать констант равновесия реакции СО + 2Н₂ = СН₃ОН_г

при 800  К, если ,и мольные теплоемкости газов:

Решение

Определяем тепловой эффект по уравнению Кирхгофа:

Константу равновесия определяем по формуле

Пример 18

Константа равновесия реакции может быть выражена уравнением

Определить тепловой эффект этой реакции при 1000 К и K_Р.

Решение

Зависимость константы равновесия от температуры описывается уравнением изобары:

.

Для определения ∆Н необходимо продифференцировать уравнение по температуре и полученную зависимость умножить на 2,303R T² .

3.3. Расчет равновесий по таблицам стандартных величин и методом Темкина – Шварцмана

Стандартное изменение изобарного потенциала выражается уравнением

.

Отсюда

или

.

Для расчета константы равновесия при любой температуре используют уравнение

,

где

Подставляя значения ив уравнение дляlgK_p, T и преобразуя его, можно получить

,

где М₀, М₁, М₂ и М_–2 – функции температуры.

; приn ≠ 0.

Указанные коэффициенты могут быть найдены по таблице, составленной М.И. Темкиным и Л.А. Шварцманом. Расчеты при использовании метода Темкина – Шварцмана значительно упрощаются.

Таким образом, для расчета константы равновесия по стандартным термодинамическим данным необходимо:

1. Найти в справочной литературе для всех участников реакции:иа_-2.

2. Рассчитать для реакции и Δа_-2 путем вычитания из суммы соответствующих величин для конечных продуктов суммы этих величин для исходных веществ с учетом стехиометрических коэффициентов уравнения химической реакции.

3. Найдя по таблицам Темкина – Шварцмана значения М₀, М₁, М₂ и М_-2 для своей температуры Т, рассчитать K_p, T.

Пример 19

Вычислить константу равновесия по методу Темкина –Шварцмана для реакции в газовой фазе при 1200 К. Полученное значение константы равновесия сравнить с экспериментальным

Решение

Находим из справочника значения и Δа₂ для Н₂, СО, СО₂ и СН₄. Данные записываем в виде таблицы:

Вещество			а0	а1 .103	а2 .106	а–2 .10-5
			Дж/(моль·К)
СО	-110,50	197,40	28,41	4,10	–	-0,460
Н2	0	130,60	27,28	3,26	–	0,502
СН4	-74,85	186,20	17,45	60,46	1,17	–
СО2	-393,50	213,60	44,14	9,04	–	8,530

По данным таблицы вычисляем:

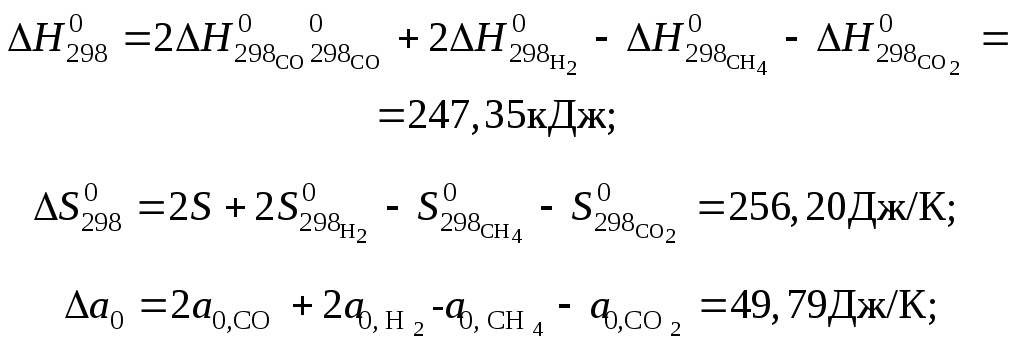
По таблице Темкина – Шварцмана при Т = 1200 К находим:

М₀ = 0,641, М₁ = 0,339 · 10³ , М₂ = 0,203 ^.10⁶ , М_-2 = 0,318 ^.10^-5 .

По приведенной выше формуле находим:

Таким образом, K_р, 1200 = 3,127·10³, вычисляем расхождение между расчетными и экспериментальными данными:

Список литературы