3.19. Точка перетину прямої з площиною

Якщо пряма не паралельна площині, то вони перетинаються в одній точці. Щоб знайти точку перетину необхідно розв’язати систему їх рівнянь

Це зручніше зробити, якщо рівняння записати в параметричній формі

і підставити ці вирази в рівняння , тоді одержимо

За знайденим значенням із (34) знаходимо координатиточки перетину.

Приклади

1.Знайти точку перетину прямої з площиною.

Розв’язання. Запишемо рівняння прямої в параметричному вигляді: Підставимо вирази дляx, y, z в загальне рівняння площини

Звідки

2. Знайти точку N симетричну з точкою М(-1,4,2) відносно площини

Розв’язання. Спочатку складемо рівняння прямої, яка проходить через точку М(-1,4,2) перпендикулярно до площини. За напрямний вектор можна взяти нормальний векторданої площини (див. умову (33) попереднього параграфа). Отже, маємо

Знайдемо точку перетину знайденої прямої з площиною. З рівняння прямої виражаємо і підставляємо у рівняння площини

–точка перетину прямої і площини. Ця точка є серединою між двома симетричними відносно площини точками М(-1,4,2) і N(X_N, Y_N, Z_N), тобто

Отже, симетричною з точкою М(-1,4,2) відносно заданої площини є точка N(5,6,4).

Задачі для самостійного розв’язання

1. Довести, що пряма паралельна площиніа пряма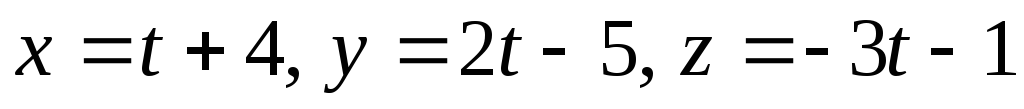перпендикулярна цій площині.

2. Знайти точку перетину прямої з площиною, яка проходить через точку М(0,3,-5), перпендикулярно до цієї прямої.

3. Скласти рівняння площини, яка проходить через точку А(-2,3,3) і перпендикулярна прямій

4. Через точку М₀(1,-3,5) провести пряму, перпендикулярно до площини

5. Знайти координати основи перпендикуляра, опущеного з точки М(5,0,8) на площину

6. Знайти точку А₁ симетричну з точкою А(7,5,-8) відносно площини

7. Довести, що прямі таперетинаються, та скласти рівняння площини, на якій вони лежать.

8. Довести, що прямі іпаралельні, та знайти рівняння площини, в якій вони лежать.

9. Знайти точку А_1, яка симетрична з точкою А(4,-2,1) відносно прямої

10. Дано дві мимобіжні прямі: і. Необхідно: 1) скласти рівняння площини, яка проходить через пряму₁ і паралельна прямій ₂; 2) знайти відстань між прямими.

Вказівка. 1) Знайти вектор Рівняння площини знаходиться за точкою М₁(6,-1,0) та нормальним вектором . 2) Відстань між прямими збігається з відстанню від точки М₂(1,7,5) до знайденої в п. 1) площини.

Відповіді: 2. 3. 4. 5. 6. 7. 8. 9. 10. .

20. Криві другого порядку

Рівняння вигляду

де хоча б один з коефіцієнтів абовідмінний від нуля, називається алгебраїчним рівняннямпершого порядку, або першого степеня відносно змінних і.

Рівняння (35) завжди описує пряму лінію.

Алгебраїчним рівнянням другого порядку називається всяке рівняння вигляду

де хоча б один з коефіцієнтів .

Лінії, координати точок яких задовольняють рівняння (36) називаються лініями другого порядку. До ліній другого порядку відносяться: еліпс (зокрема коло), гіпербола, парабола. Вони описуються рівнянням вигляду (36). Однак не кожне рівняння другого порядку завжди описує одну із згаданих ліній. Може, наприклад, вийти так, що рівняння вигляду (36) описує пару прямих ліній або не визначає жодного реального об’єкту.

Приклади.

1.Рівняння описує коло.

2.Рівняння описує параболу.

3.Рівняння розпадається на дві пряміі, що перетинаються.

4.Рівняння , тобторозпадаються на дві паралельні пряміі.

5.Рівняння , тобторозпадається на дві прямі, що збігаються.

6.Рівняння має своїм розв’язком тільки одну точку.

7.Рівняння не описує в області дійсних чисел ніякого геометричного місця точок.

Додамо ще, що при відповідному виборі декартової системи

координат рівняння (36) для кривих другого порядку набувають простий, так званий канонічний вигляд. Далі розглянемо коротко кожну із кривих другого порядку.