3.7.Канонічне та параметричне рівняння прямої

Нехай в системі координат задана точкаі ненульовий вектор(рис.7).

рис.7.

Необхідно скласти рівняння прямої, що проходить через точку паралельно вектору, що називаєтьсянапрямним вектором. Довільна точка належить цій прямійтоді і тільки тоді, коли. Оскільки вектор– заданий, а вектор, то згідно з умовою паралельності, координати цих векторів пропорційні, тобто

Співвідношення (7) називається рівнянням прямої, що проходить через задану точку у заданому напрямку або канонічним рівнянням прямої.

Звернемо увагу, що до рівняння вигляду (7) можна перейти, наприклад, від рівняння пучка прямих (4)

,

або від рівняння прямої за точкою та нормальним вектором (1)

Зауваження. Вище припускалось, що напрямний вектор – ненульовий, але може трапитись, що одна з його координат, наприклад,. Тоді вираз (7) формально запишеться

який, взагалі кажучи, не має смислу. Однак приймають і отримують рівняння прямої перпиндикулярної осі. Дійсно із рівності видно, що пряма визначена точкоюі напрямним вектором, перпиндикулярним осі. Якщо ж в цьому рівнянні звільнитись від знаменника, то отримаємо, або– рівняння прямої, перпендикулярної осі. Аналогічно було б отриманодля вектора.

Щоб перейти до параметричного рівняння прямої, прирівняємо кожен із дробів (7) до параметра . Оскільки хоча б один із знаменників в (7) відмінний від нуля, а відповідний чисельник може набувати довільні значення, то область зміни параметра– вся числова вісь. Отримаємо

або

Рівняння (8) називається параметричним рівнянням прямої.

Приклади

1. На прямій лінії заданої рівнянням , знайти точкуM(x,y), що знаходяться від точки цієї прямої на відстані 10 одиниць.

Розв’язання. Нехай –шукана точка прямої, тоді для відстані запишемо. За умовою. Оскільки точканалежить прямій, що має нормальний вектор, то рівняння прямої можна записати

Тоді відстань . За умовою, або. З параметричного рівняння

Відповідь:

2. Точка рухається рівномірно з швидкістюв напрямку векторавід початкової точки. Знайти координати точкичерезс від початку руху.

Розв’язання. Спочатку знайти одиничний вектор . Його координати це напрямні косинуси

.

Тоді вектор швидкості

Канонічне рівняння прямої тепер запишется

параметричне рівняння.

Після чого скористатись параметричним рівнянням прямої при . Відповідь:.

3.8.Основні задачі на пряму лінію

а) Рівняння прямої за двома точками ізнаходимо з канонічного рівняння (7) оскільки напрямний вектор, то

Приклад. Записати рівняння прямої, якщо ,. Відповідь:.

б) Відстань від точки до прямої знаходиться за формулою

Дійсно, з рис. 8 зрозуміло, що

,

Рис. 8.

де – довільна точка прямої. Вектор.

Тоді Але із загального рівняння прямої, томуа. Отже,

отримуємо (9).

Наприклад, відстань від точки до прямоїза формулою (9) дорівнює

в) Кут між двома прямими іспочатку знайдемо, коли їх рівняння мають вигляд (див. рис.9)

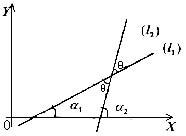
Рис.9

Оскільки а, то

Отже,

• формула тангенса кута між двома прямими.

Зауваження. З рис.9 видно, що між прямими і- два кути: один – гострий, другий – тупий. Згідно формули (11)- це той кут між прямимиі, на який потрібно повернути прямупроти годинникової стрілки від носно їх точки перетину до суміщення її з прямою. У формулі (11) для однозначності нагадує стрілка, записана зверху.

Приклад. В рівнобедреному прямокутному трикутнику АВС відома вершина прямого кута С(-1,2) і рівняння гіпотенузи АВ . Скласти рівняння катетів.

Розв’язання. Рівняння прямої, що проходить через точку С знаходимо за формулою пучка прямих , де кутовий коефіцієнтдля прямої АС ідля прямої ВС.

За умовою А=В=45, tg45=1, тому ізнаходимо за формулою (11), ураховуючи зауваження до неї.

Спочатку знайдемо і рівняння катета АС.

Оскільки поворот прямої АВ на кут 45 проти годинникової стрілки відносно точки А приводить до суміщення з прямою АС, то у формулі (11) , а. Із рівняння АВ:, тому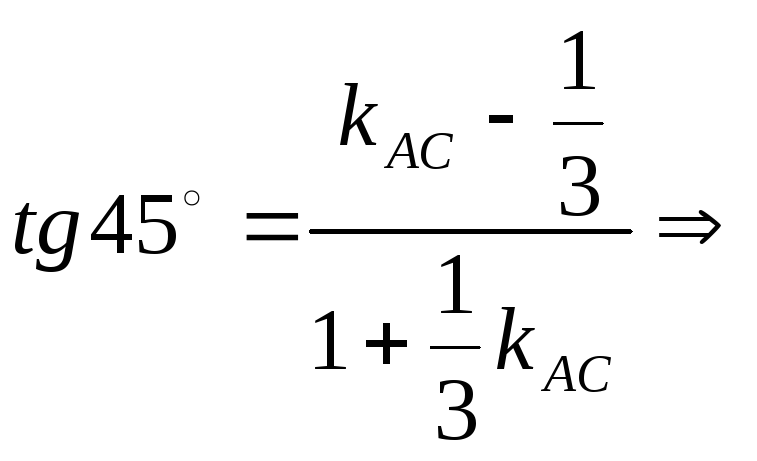

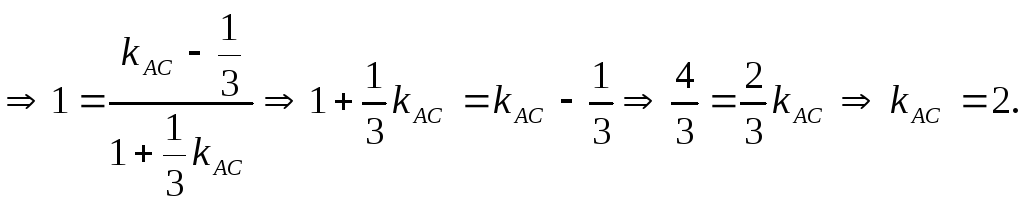
За формулою пучка рівняння прямої АС запишеться

(АС) .

Аналогічно знайдемо і рівняння ВС. При вершині В за формулою (11) відповідно беремо, а,В=45

Рівняння прямої ВС:

(ВС)

Якщо – прямі паралельні, тоі тоді

– умова паралельності двох прямих.

Якщо ж , то, а

або

- умова перпендикулярності двох прямих.

Якщо ж прямі задані загальними рівняннями

то кут між ними можна знаходити, як кут між їх нормальними екторами (див. рис. 10);

Рис.10

косинус кута між двома прямими і, заданими загальними рівняннями.

Якщо , то

– умова паралельності. Якщо ж , то

– умова перпендикулярності прямих.

г) Рівняння прямої, що проходить через задану точку паралельно прямій .

Розв’язання. Кожного разу, коли задається точка, то рівняння прямої краще знаходити за формулою (5) пучка прямих

,

де – знаходимо із загального рівняння заданої прямої і умови паралельності прямих (12).

Наприклад, скласти рівняння прямої, що проходить через точку паралельно прямій.

Розв’язання. Із загального рівняння прямої , а за умовою паралельності прямих, тоді отримуємо.

д) Рівняння прямої, що проходить через точку перпендикулярно прямій .

Із загального рівняння , а за умовою перпендикулярності маємо, тоді шукане рівняння за формулою пучка

Приклад. Скласти рівняння прямої, що проходить через точку перпендикулярно до прямої.

Розв’язання. Із . Тоді

Відповідь:

.

е) Точка перетину прямих і, якщо вони не паралельні

знаходиться як розв’язок системи

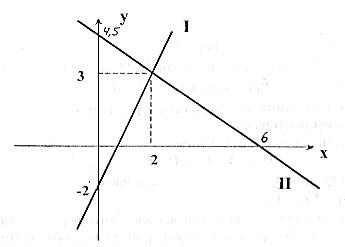
Приклад. Знайти точку перетину прямих. Зробити рисунок, побудувавши графіки.

Розв’язання. Розв’яжемо дану систему рівнянь, домноживши перше рівняння на 2 і додавши результат з другим рівнянням

Підставивши в перше рівняння маємо:

Отже, точка перетину .

Побудуємо графіки за рівняннями, що входять в систему. Побудову краще виконати у відрізках на осях