Ііі. Аналітична геометрія

3.1. Аналітична геометрія це розділ математики, в якому геометричні задачі розв’язуються алгебраїчним шляхом за допомогою методу координат.

В аналітичній геометрії геометричні місця точок або лінії задаються рівняннями, що зв’язують в даній системі координат змінні і, які називаються ще поточними координатами. Якщо в елементарній геометрії лінії та їх властивості вивчались в основному за допомогою геометричних побудов, то в аналітичній геометрії вони вивчаються шляхом дослідження рівнянь цих ліній.

Означення. Рівнянням лінії в аналітичній геометрії називається співвідношення, (або залежність між змінними і) вигляду, яке задовольняють координати довільної точкицієї лінії, а якщо точкане лежить на цій лінії, то її координати не задовольняють дане рівняння.

Наприклад.

1. Координати точки задовольняють рівняння прямої, отже, ця точка лежить на прямій. Координати точкидане рівняння не задовольняють:. Отже,не лежить на даній прямій.

2. Точка лежить на колі, оскільки, а точкане лежить на цьому колі, бо.

Пряма лінія на площині

3.2.Рівняння прямої за точкою та нормальним вектором

Нехай в системі координат задана точкаі ненульовий вектор(рис.1).

Очевидно існує єдина пряма , що проходить через точкуперпендикулярно напрямкові вектора(в цьому випадкуназиваютьнормальним вектором прямої ).

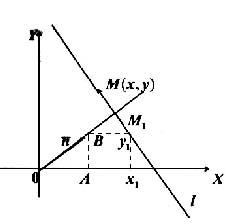
Рис.1

Доведемо, що лінійне рівняння

є рівнянням прямої , тобто координати кожної точкипрямоїзадовольняють рівняння (1), але координати точки, що не лежить на, рівняння (1) не задовольняють.

Для доведення зауважимо, що скалярний добуток векторів ів координатній формі збігається з лівою частиною рівняння (1).

Далі використаємо очевидну властивість прямої : векториіперпендикулярні, тоді і тільки тоді, коли точкалежить на. А за умовою перпендикулярності двох векторів їх скалярний добуток (2) перетворюється вдля всіх точок, що лежать на, і тільки для них. Отже, (1) – рівняння прямої.

Рівняння (1) називається рівнянням прямої, що проходить через дану точку з нормальним вектором .

Приклад. Дана точка М(4,1) і вектор Необхідно:

1) скласти рівняння прямої , що проходить через точку М перпендикулярно вектору;

2) перевірити, які з точок М₁(0,3), М₂(-6,6), М₃(3;2,5), М₄(8,-1) лежать на прямій ;

3) побудувати пряму і точки М₁, М₂, М₃, М₄.

Відповіді: 1) (х-4)+2(у-1)=0; 2) ,

3.3. Загальне рівняння прямої

Перетворимо рівняння (1)

.

Позначивши , отримаємо

— загальне рівняння прямої.

Таким чином, прямій лінії відповідає лінійне рівняння вигляду (3). Навпаки, за даним рівнянням вигляду (3), де хоча б один з коефіцієнтівівідмінний від нуля, можна побудувати пряму.

Дійсно, нехай пара чисел задовольняє рівняння (3), тобто

.

Віднімаючи останнє від (3), одержимо співвідношення , яке визначає пряму за векторомі точкою.

Приклади

1.Скласти загальне рівняння прямої, що проходить через точку перпендикулярно вектору.

Відповідь: .

2.Задані точки і. Скласти загальне рівняння прямої, що проходить через точкуперпендикулярно вектору.

Відповідь: .