11. Среднее значение физической величины. Операция физической величины.

Как мы уже знаем, квадрат модуля волновой функции определяет плотность вероятности состояния микрочастицы в произвольный момент времени. Однако, возникает вопрос, каким образом произвольная физическая величина L будет связана с волновой функцией.

Квантовая механика утверждает, что зная волновую функцию и, зная оператор 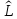, мы можем рассчитать среднее значение L по формуле: .

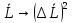
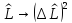
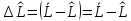
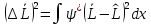
Вернемся к (*): .

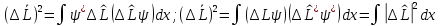12. Уравнение на собственное значение. Собственная функция и собственное значение оператора физической величины. Спектр собственного значения.

Отметим, если мы произведем единичные измерения физической величины L, то её дисперсия по определению равна нулю (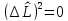), поскольку .

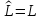Тогда из предыдущего параграфа следует, что

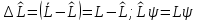– этот оператор уравнения называется уравнением на собственное значение. В квантовой механике, в подавляющем большинстве случаев, в качестве оператора 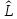выступает какой-либо дифференциальный оператор первого или второго порядка. Например: .

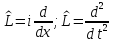Решение этого оператора уравнения, обязательно удовлетворяющее свойствам конечности, например: однозначность волновой функции 𝛙. …. этим требованиям, как правило, приводим к тому, что решим, возможно, не при любых произвольных значениях физической величины L, а лишь при избранных: 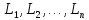. Такие значения называют собственными значениями 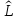. Ряд собственного значения часто называют спектром. Он может быть дискретным, может быть непрерывным, может состоять из определения полос. Например: энергия электрона L=E – энергетический спектр. Отметим, что каждому собственную функцию, которая в итоге образует спектр собственной функции .

В квантовой механике постулируется, что идеальный прибор измерения физической величины L, не может показывать иных значений, кроме собственных значений этой величины.

13. Основные свойства собственных функций.