Глава 2: математический аппарат квантовой механики.

9. Волновая функция и её основные свойства.

Хорошо известно, что в квантовой механике состояние любой частицы определяется тремя координатами и тремя проекциями импульса, то есть шестью скалярными функциями. Если мы имеем уравнения движения или закон движения (уравнения Ньютона, Лагранжа, Гамильтона) и знаем начальные условия, то есть местоположение частицы в начальный момент времени, то решив уравнения движения, мы будем знать траекторию, а, следовательно, и состояние частицы в любой момент времени, такой подход называется классическим детерминизмом.

В квантовой механике состояние частицы принято описывать так называемой волновой функцией: ; . Зная волновую функцию, мы можем определить вероятность состояния микрочастицы следующим образом: .

В самом простейшем случае под состоянием микрочастицы мы будем понимать её местоположение в пространстве. В квантовой механике постулируется, что волновая функция подчиняется уравнению Шрёдингера, решив которое, с учётом начального значения волновой функции, мы получим волновую функцию в произвольный момент времени, то есть 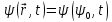; 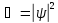=> , то есть вероятность состояния микрочастицы в любой произвольный момент времени зависит от вероятности состояния в начальный момент времени, такой подход называется квантовый детерминизм.

Рассмотрим основные свойства волнов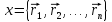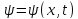ой функции (; ; ; ): 1) нормировка волновой функции .

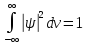Волновая функция в квантовой механике обязана, подчинятся трем основным требованиям: 1. непрерывность; 2. однозначность; 3. конечность.

Для волновой функции считается справедливым принцип суперпозиции состояния. Суть его в следующем: если микрочастицы могут находиться в состоянии волновой функции , то эти частицы могут находиться в состоянии .

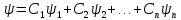Отметим, что введенная здесь волновая функция зависит от координат времени, но не зависит от импульсов частиц. Это связанно с принципом неопределенности Гейзенберга, из которого следует, что координаты и импульс являются взаимоисключающими переменными. Представление волновой функции в виде: 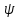= 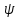(x, t) называется x представлением (<x>) или координатным представлением. Однако, в квантовой механике существует возможность использовать и другие переменные в качестве основных 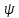= (p, t), 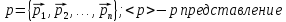(импульсное представление.

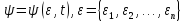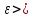, <-энергетическое представление (эпсилон представление).

Плотность представления - ; dW.

Различные виды представления волновой функции связаны между собой, например: .

10. Изображение физических величин операторами. Основные свойства операторов в квантовой механике.

Пусть имеется . Под оператором мы будем понимать действие (набор действий), которое необходимо выполнить над функцией стоящей справа от него: ; .

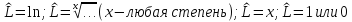Однако, в квантовой механике применяют не любые операторы. Операторы, применяемые в квантовой механике должны обладать следующими, двумя свойствами: 1) свойство линейности . Свойство линейности оператора следует из принципа суперпозиции волновой функции. Пример линейного и не линейного оператора: 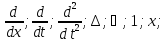2) свойство самосопряженных операторов в квантовой механике называется самосопряженным, если выполняется следующее равенство: 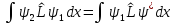(i- самосопряженное, –не самосопряженное).

Поскольку оператор 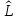для величины L может быть комплексной функцией, свойство само сопряжённости необходимо для того, чтобы отображал реальную физическую величину L.

Для оператора x – два математических действий: сложение и умножение. Сложение: если имеются два оператора 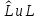, то под суммой этих операторов мы будем понимать , для … выполняется следующее равенство . Умножение: пусть два оператора , тогда под произведением этих двух операторов мы будем понимать такой оператор , для которого выполняется следующее выражение: .

Отметим, что операция умножения в общем случае, в квантовой механике не является коммутационной. Это означает, что оператор в общем случае не равен ().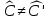

Оператор 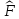называется коммутатором : .

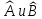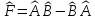Примеры: ; ;

;

.
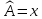
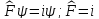