7. Волны де-Бройля. Дисперсия волн де-Бройля. Статическая интерпретация волн де-б.

1923 г. – де-Бройль основываясь на результат экспериментов по дифракции микрочастиц, предложил связать с любой свободной частицей плоскую монохроматическую волну.

, ;

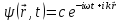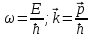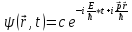
Чтобы проверить утверждения де-Бройля, необходимо вычислить фазовую скорость этой волны и сравнить её со скоростью частиц.

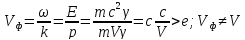
После этого возникает идея связать со свободно движущейся частицей некий волновой пакет, который можно представить в виде:

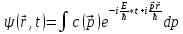
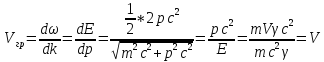
Отсюда, на первый взгляд, следует, что любой свободно движущейся частице можно поставить в соответствии волновой пакет. Однако, если рассмотреть волновой пакет в пространстве, то мы увидим наличие дисперсии волн, то есть зависимость фазовой скорости от длины волны:

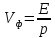
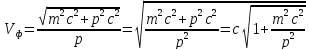
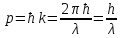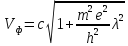; . Отсюда мы видим, что с ростом длины волны фазовая

волнам де-Бройля дал немецких физик М. Борн. М. Борн подметил одну существенную особенность скорость возрастает и наоборот. Следовательно, с течением времени волновой пакет будет расплываться в пространстве. Таким образом, учитывая стабильность многих микрочастиц (в частности электрона), мы видим, что волновой пакет так же нельзя поставить в соответствии свободно движущейся частице.

Правильную интерпретацию в экспериментах по получению дифракционной картины в экспериментах по рассеянию частиц. Дифракционная картина получалась наиболее четкой и явной лишь в том случае, когда в процессе рассеяния принимают очень большое число микрочастиц. Это навело Борна на мысль о том, что проявление волновых свойств связано с понятием вероятности.

Чтобы пояснить эту мысль, приведем рассуждения самого Борна: если в процессе рассеяния участвуют всего несколько микрочастиц, то на фотопластинке будет возникать картинка аналогичная мишени в тире, сделанная плохим стрелком. Лишь только когда число микрочастиц участвующих в рассеянии станет достаточно большим, на фотопластинке будут появляться концентрические светлые и темные области, аналогичные дифракционной картине. При этом Борн предположил, что амплитуда плоской волны де-Бройля пропорциональна вероятности обнаружения микрочастиц в какой-то конкретной точке пространства.

Отсюда следует простое объяснение так называемой дифракционной картины: темные круги – область с минимальной вероятностью обнаружения микрочастиц, а светлые – с максимальной (рис. Блохинцев).

Непосредственную связь вероятности обнаружения микрочастиц с плоской волны де-Бройля, М. Борн предложил: (

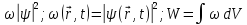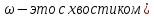
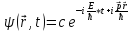– уравнение плоской волны де-Бройля.

8. Соотношение неопределенностей Гейзенберга.

Отметим, что 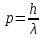в левой части содержит характеристику частицы импульса p, а в правой – характеристику волны 𝛌. Именно эта формула нагляднее всего свидетельств о корпускулярно-волновом дуализме в отношении частиц и более широком смысле объясняет вероятностные свойства микромира.

В рамках концепции корпускулярно-волнового дуализма частиц запишем известное соотношение из теории волн: 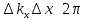. Это соотношение записано для произвольного волнового пакета и 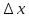- область локализации волнового пакета в обычном пространстве, а 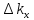- число волновых чисел из которых состоит волновой пакет или, другими словами, область локализации волнового пакета в пространстве волновых чисел.

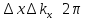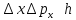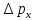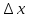Немецкий физик Гейзенберг применил соотношение: к волновому пакету де-Бройля, до множил на ħ => . Здесь – неопределенность импульса частицы, а – неопределенность координаты. Это соотношение получило название соотношение неопределенностей Гейзенберга и более строго оно записывается так: 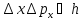. Гейзенберг интерпретировал данное соотношение следующим образом: если мы измеряем локализацию частицы, то есть, её местоположение, то, в результате, многочисленных измерений, мы получим некоторое среднее значение x₀. Результат же конкретного измерения идеальным прибором (прибором без погрешности) будет давать значения (интервал) отсюда 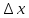и получило название неопределенной координаты.

Точно так же рассуждения можно провести и для неопределенности импульса .

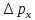Из соотношения неопределенностей следует, что, если мы попытаемся максимально точно измерить местоположение частицы (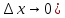, то неопределенность импульса проекции будет бесконечно возрастать, и мы ничего не сможем сказать о его численном значении. Наоборот, если мы стремимся максимально точно измерить импульс, то есть, 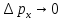из соотношения неопределённости следует, что 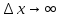. Последнее означает, что мы не сможем узнать, в каком месте пространства находится частица.

Соотношение неопределенности Гейзенберга фактически отражает вероятностный характер поведения микрочастиц. С математической точки зрения соотношение неопределенностей означает, что координата и проекция импульса являются взаимоисключающими переменными и одновременно не могут быть измерены точно (отметим, что речь идет с использованием абсолютно точного прибора). В квантовой механике, кроме приведенных выше, существуют и другие пары взаимоисключающих переменных 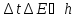. Здесь . 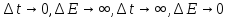Кроме этого, нельзя одновременно измерить 2 проекции момента импульса на разные оси координат.