Зубенко, Омельчук - Програмування. Поглиблений курс

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

Ui =Ui −1 o X . ΩL -терми системи називаються регулярними вираза-

ми, а їхні значення в – регулярними мовами. Для спрощення запи- су регулярних виразів використовується пріоритет операцій (відпові- дає порядку операцій у Ωf ), можуть опускатися символ множення o і

фігурні дужки в одноелементних множинах. Наприклад,

{c1,c2}c3 = {c1,c2}o{c3} = {c1c3,c1c3}.

Приклад 1.19. Регулярні мови.

Вирази: 1) {a}* ; 2) a {ba}* ; 3) {aa}* задають регулярні мови:

1){an : n ≥ 0};

2){ε,a,ba,baba,bababa,K};

3){a2n : n ≥ 0}■

Регулярні вирази широко використовуються в сучасних мовах про- грамування22, при побудові лексичних аналізаторів тощо.

Системи алгоритмічних алгебр (САА). Були введені В.М. Глушковим у зв'язку із задачами синтезу й аналізу дискретних перетворювачів інформації та поклали початок застосуванню алгеб- ричних методів у проектуванні ЕОМ і програмуванні.

Сигнатура Ω САА має такий склад:

Ωs = {func,pred}, Ωc = {id,f1,..., fn : func, p1,..., pm : pred},

22 Наприклад, у таких мовах, як XML, HTML, Perl, Python та інших мовах WEB- програмування.

81

ПРОГРАМУВАННЯ

Зафіксуємо певну множину A . Нехай F (A) позначає сукупність усіх відображень типу A → A , а P (A) – усіх предикатів на A . Відо- браження та предикати в САА називають відповідно операторами й умовами. Нехай iA ,F1,...,Fn – одиничний і довільні оператори з F (A), а P1,...,Pm – умови з P (A). Визначимо САА як Ω -систему FP із мно- жинами сортів ΩS = {F(A),P(A)} , констант ΩC = {iA ,F1,...,Fn ,P1,...,Pm }, предикатів ΩP = {=, } і операцій ΩF = {o,(→),{→},•,¬, , }. В останній

сукупності o – множення операторів, далі йдуть відповідно компози- ції розгалуження, ітерації, множення оператора на умову, диз'юнкції, кон'юнкції й заперечення.

Як і в регулярних мовних виразах, для спрощення регулярних САА- термів використовується пріоритет операцій (відповідає порядку в

¬p1{ p2 → f2 } p4 – мікропрограму (¬({ p2 → f2 } • p1) p4 ).

Якщо сигнатуру САА доповнити символами чотирьох однотипних композицій ↑,↓,→,[] : pred× func a func – відповідно композицій зву-

ження, обмеження, обходу й повторення, а також символом компози- ції недетермінованого вибору ||: pred× func× pred× func a func , то

отримаємо сигнатуру ΩRAA = (Ωs ;Ωc ,Ωv ,Ωf ,Ωp ) регулярної алгоритмі-

чної алгебри.

Вільні Ω -системи. При вивченні й моделюванні Ω-систем важли- ва роль належить вільним Ω -системам. Носієм вільної системи да- ного типу є сукупність T (Ω) усіх можливих типізованих Ω -термів,

82

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

дносно всіх операцій-конструкторів fˆi сигнатури Ωf . Уся сукупність T (Ω) за означенням поділена на типи. Покладемо, що Tk – сукупність

ється довільна Ω -система на універсумі термів T (Ω) , операції та предика-

ти якої є операціями-конструкторами термів і предикатами на термах відповідних типів.

морфна певній фактор-системі /σφ вільної системи типу .

Поняття гомоморфізму багатосортних систем Ω -системи певного типу не відрізняється від аналогічного поняття для звичайних систем. Єдине, що вимагається від гомоморфізму багатосортних систем, – щоб він додатково зберігав тип елементів.

Теорема 1.4 (про вільні Ω -системи). Відображення φ : Ωc → ΩC таке,

Покажемо, що φ – гомоморфізм. Дійсно, за означенням

fˆiτi (ti1,...,tin )φ = fiτi (ti1,...,tin )φ /*означення fˆiτi */ = Fiτi (ti1φ,...,tin φ)/*Def φ*/.

83

ПРОГРАМУВАННЯ

Нехай ϕ : T (Ω) → A – інший гомоморфізм і ci φ = ci ϕ , i ≥1. Покажемо, що φ = ϕ . Застосуємо структурну індукцію для термів. База індукції

=Fiτi (ti1φ,...,tin φ) /*індуктивне припущення*)/ =

=fˆiτi (ti1 ,...,tin ) φ /*означення φ-гомоморфізму*/.

Відображення φ : T (Ω) → A є відображенням "на", тому що сукуп- ність ΩC за умовою є твірною системи A ■

Як свідчить теорема 1.1, вибираючи в кожному фактор-класі /σφ

певний Ω -терм за канонічний представник усього класу, завжди мо- жна отримати термальну копію будь-якої системи A й перейти від абстрактних елементів носія A до конкретної множини Ω -термів. Це відкриває універсальний шлях до словарного моделювання будь-яких Ω -систем. Зрозуміло, він не завжди забезпечує необхідний рівень ефективності моделей, але важливо, що такий шлях існує і ним мож- на скористатися.

Нестандартні алгебричні системи. Як зазначалось у підрозд. 1.1,

потреби метаматематики й програмування привели до необхідності узагальнення понять звичайної n -арної операції й алгебричної системи. Одне з найпростіших із них ми вже розглянули – поняття багатосортної операції і Ω -системи. Наступними узагальненнями є: 1) перехід від векторів фіксованої довжини до довільних послідовностей (як скінченних, так і нескінченних), а також 2) до довільних скінченних і нескінченних індексованих сукупностей елементів. Дослідження в цих напрямах були розпочаті польськими математиками й логіками всередині минулого сторіччя. Для нових узагальнених операцій було побудовано алгебричну теорію, аналогічну традиційній (теореми про гомоморфізми, конгруенції, вільні алгебри тощо). Деякі з цих результатів викладено в [105]. Потужним імпульсом для прискорення й розвитку подібних результатів стали дослідження з денотаційної та композиційної семантики мов програмування (див.

84

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

літературу для СР). Ми покажемо, як застосовуються узагальнені операції при описі семантики вихідних систем у підрозд. 2.1.2.

1.4.4. ДЕЯКІ ПРИКЛАДНІ БАГАТОСОРТНІ Ω -СИСТЕМИ

Кілька важливих прикладних Ω -систем уже було розглянуто вище. Продовжимо їхній розгляд.

Матрична алгебра. Нехай R – певна сукупність чисел. Числовою матрицею розміром n ×m над R називається вектор A довжиною n , компоненти якого називаються рядками та є, у свою чергу, число- вими векторами довжиною m над R . Для позначення елементів мат-

риці використовують подвійну індексацію й пишуть A = (aij )ni =1mj =1 , де

У результаті множення матриці на скаляр і вектор отримаємо ма-

Додавання матриць повертає матрицю того самого розміру:

Множення матриць повертає матрицю розміром n ×k :

У матричній алгебрі є багато законів, що виконуються для чисел множини R. Наприклад, додавання цілих матриць асоціативне й ко- мутативне, множення асоціативне тощо (вправа 13).

Реалізація й аналіз алгоритмів матричної алгебри розглядаються в підрозд. 4.2.

85

ПРОГРАМУВАННЯ

Списки, стеки й черги. Кортежі, елементами яких можуть бути інші кортежі, називаються списками. Зафіксуємо певну множину U , елементи якої називаються атомами. Побудуємо сім'ю множин Ui :

U0 =U , Ui +1 =Ui Ui* , i > 0 . Отже, U1 складають атоми й кортежі з атомів. Останні називають лінійними списками. До U2 додаються ко-

ртежі кортежів і т. д. Сукупність списків Lst =U ∞ визначається як

def ∞

U ∞ = i =1Ui \U0 .

Приклад 1.20. Списки.

Нехай U = {A,B,C,+,−,*,/,[,]}, тоді

A – атом;

[ ] – порожній список; [A] – лінійний список;[A] – нелінійний список;

[A,+,B ],*,C , *,[+,A,B ],C ,[A,B,+,C,*].

Останні три списки подають різні форми термів для арифметично- го виразу (A + B )* C . Це відповідно (A + B )* C – інфіксна форма;

*(+(A,B ),C ) – префіксна форма та A B +C * – ОПЗ. Звичайна пост- фіксна форма цього виразу має вигляд ((A,B )+,C )* ■

Основними операціями на списках є: cons :U ×Lst → Lst – дода- вання ліворуч елемента до списку; конкатенація списків; вставлення й вилучення елементів зі списку; пошук елементів у списку; перевір- ка, чи не є список порожнім. Визначимо операцію cons : для атома

push(a,[a1 ,...,ak ])= [a1 ,...,ak ,a] – додати елемент у стек; read ([a1 ,...,ak ])= (k > 0 → ak |#) – прочитати елемент у стеку;

pop([a1 ,...,ak ])= (k > 0 → [a1 ,...,ak −1]|#) – зняти елемент зі стеку;

86

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

empty (s) s = [ ] – перевірка, чи є стек порожнім.

Як бачимо, зі стеку можна видалити лише той елемент, що був до-

даний останнім (останнім прийшов – першим пішов), тому стеки ще називають списками LIFO (англ. – Last-In, First-Out).

Сукупність Qn черг, як і стеків, утворюють лінійні списки з U1 , тобто Qn =U1 \U . Вони мають ті самі операції, що й стеки, але відріз- няються означенням операцій read : St →U та pop : St → St :

read ([a1 ,...,ak ])= (k > 0 → a1|#);

pop([a1 ,...,ak ])= (k > 0 → [a 2 ,...,ak ]|#).

Із черги можна видалити лише той елемент, який перебуває в ній найдовше (першим прийшов – першим пішов), тому черги також на-

зивають списками FIFO (англ. – First-In, First-Out).

Програмні моделі списків, стеків, черг і реалізація основних опера- цій з ними розглядаються в підрозд. 4.3.

Орієнтовані графи. Мультиграфи. Мережі. Орієнтовані графи

(надалі – просто графи) є певною спеціалізацією поняття бінарного відношення. До цього розглядались найбільш загальні властивості бі- нарних відношень. Тепер ми зробимо наступний крок і, обмежившись скінченним відношенням, розглянемо тонші зв'язки між його елемен- тами. Саме завдяки цим зв'язкам графи знайшли широке застосу- вання в інформатиці. Зокрема це стосується подання складнострук- турованої інформації. Фактично ми хочемо перейти від загального поняття до глибшого розглядання певного його фіксованого смисло- вого варіанта. При подібних переходах семантика понять залишаєть- ся незмінною, а от синтаксис і термінологія часто підлаштовуються під нові постановки задач – достатньо згадати перехід від загального поняття кортежу до його спеціалізації у вигляді векторів, матриць, слів, списків, черг, стеків.

Графом називається пара G = (V ,R ), де V – сукупність вершин, а R G ×G – скінченне бінарне відношення на V , елементи якого на- зиваються ребрами. Про ребро (a,b) R кажуть: 1) воно зв'язує вер-

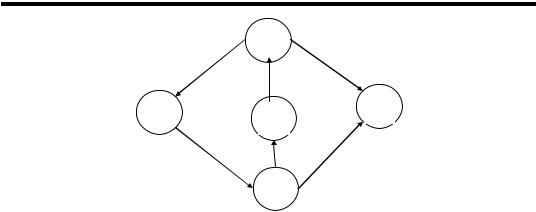
шину a з вершиною b ; 2) a є початком ребра, а b – його кінцем; 3) ребро виходить із вершини a і заходить у вершину b . Графи та їхні фрагменти зручно подавати графічно, для чого на площині виби- рають точки-вершини та з'єднують їх стрілками-ребрами (рис. 1.6):

87

ПРОГРАМУВАННЯ

5

Рис. 1.6

Граф називається порожнім, коли порожньою є одна з двох його складових. Якщо порожня сукупність ребер, то в графічному поданні будуть відображені тільки вершини, якщо ж порожньою є й сукуп- ність вершин, то графічне подання буде теж порожнім. Однак у будь- якому разі слід пам'ятати, що, незалежно від подання, порожній граф має такий самий статус, як і всі інші графи. Шляхом у графі назива- ється послідовність ребер, в якій початок кожного наступного ребра збігається з кінцем попереднього. Ко-шлях – це послідовність ребер, в якій кінець кожного наступного ребра збігається з початком попере- днього. Зв'язок – послідовність шляхів і ко-шляхів така, що початок кожного наступного члена збігається з кінцем попереднього. Цикл – це скінченний шлях, в якому початок і кінець збігаються. Шлях (ко- шлях) максимальний, якщо його не можна продовжити. Початкова вершина – це вершина, в яку не входить жодне ребро. З кінцевої вер- шини не виходить жодного ребра. Ізольована вершина є одночасно й початковою, і кінцевою. Граф зв'язний, якщо між кожними його дво-

ма вершинами є зв'язок. Підграфом графа G = (V ,R ) називається граф G = (V ′,R′), де V ′ V , а R′ R . Підграф графа є його фрагмен-

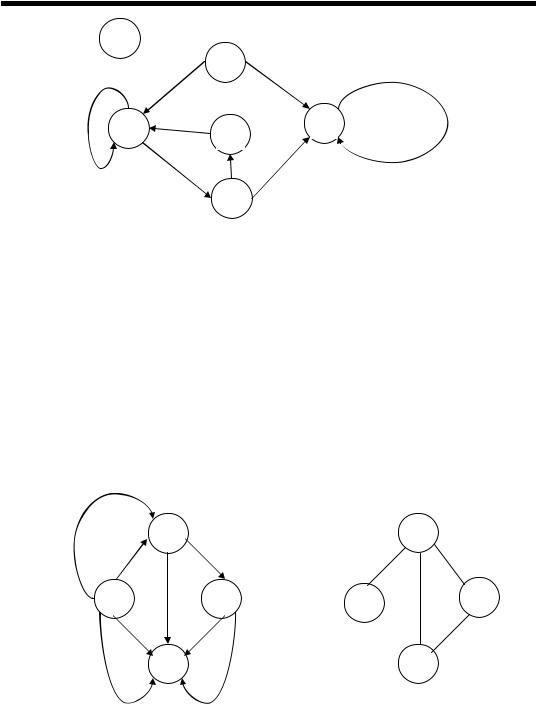
том, якщо він містить усі зв'язки графа між вершинами фрагмента. Проілюструємо введені поняття на прикладі незв'язного графа. Приклад 1.21. Розглянемо граф, зображений на рисунку. Він має

такі цикли: 2 − 5 − 3 − 2; 2 ; 4 – останні два є петлями.

Початкові вершини – 1 та 6. Кінцеві вершини – 4 та 6. Ізольована вершина – 6. Підграф, що містить вершини 1− 2 − 3 − 4 − 5 і всі ребра, зв'язний.

88

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ

6

1

4

3

5

■

Неорієнтованим називається граф G = (V ,R ) із симетричним від-

ношенням R . У зображенні такого графа на площині дві стрілки, що з'єднують певну пару вершин, замінюють однією лінією без напрямку

(див. прикл. 1.22).

Мережа – зв'язний граф без циклів.

Зважений граф – трійка (G,α,β), де G – граф, α – функція, облас- тю визначення якої є сукупність вершин G , β – функція, областю ви-

значення якої є сукупність ребер G .

Мультиграф – це граф, ребра якого проіндексовані натуральними числами. На відміну від графа, у мультиграфі може бути кілька ребер з однаковими початками й кінцями. У графічному зображенні таким ребрам відповідають різні стрілки.

Приклад 1.22. Зважені мультиграф (а) і неорієнтований граф (б):

89

ПРОГРАМУВАННЯ

Розгляду й реалізації деяких важливих алгоритмів на графах при- свячено підрозд. 4.6.

Дерева. Деревом називається граф, в якому існує початкова вер- шина – корінь, з якої в будь-яку іншу вершину існує рівно один шлях. Вершини дерева називаються вузлами.

Лема 1.5 (про дерево). Граф є деревом коли виконуються умо- ви: 1) у графі є тільки одна початкова вершина; 2) у будь-який вузол входить рівно одне ребро; 3) усі шляхи скінченні.

Доведення. Див. вправу 33 ■

Кінцеві вершини дерева називаються листками. Нескладно впев- нитись, що будь-який зв'язний фрагмент дерева є деревом, яке нази- вається піддеревом із коренем у даному вузлі. У бінарному дереві ко- жне піддерево складається з кореня, з'єднаного з двома піддеревами, одне або два з яких (у випадку листків) можуть бути порожніми. За- звичай ці два піддерева впорядковані між собою, одне з них назива- ється лівим, а друге – правим. Висотою дерева називається найбіль- ша з довжин його максимальних шляхів, тобто найбільша відстань від кореня до листка в дереві. Нехай на множині вузлів дерева задано певний лінійний порядок (V ,p). Бінарне дерево називається деревом

пошуку, якщо в ньому для кожного вузла вершини лівого піддерева менші за нього, а вершини правого – більші. Відомо, що час перевір- ки, чи належить даний елемент дереву пошуку, не перевищує його висоти. Збалансовані дерева – це дерева, в яких для будь-якої верши- ни кількість елементів у лівому й правому піддеревах відрізняється не більше ніж на 1. Зрозуміло, що для збалансованого дерева в загально- му випадку час пошуку кращий. Проте іноді в дереві можуть бути зо- всім відсутні ліві або праві піддерева. Такі дерева називаються виро- дженими. Висота їх дорівнює кількості вузлів у дереві. Для таких де- рев пошуку пошук елемента перетворюється на звичайний послідов- ний пошук. Тому інколи при кожному вставленні елемента в дерево пошуку дерево корегують так, щоб воно було збалансованим.

Проілюструємо введені поняття.

Приклад 1.23. На рисунку зображено дерево з початковою вер- шиною (вузлом) 1 і листками 5 , 6 , 7 , 9 (а). Максимальні шляхи в ньому: 1− 2 − 5 , 1− 2 − 6 , 1− 3 − 7 , 1− 4 − 8 − 9 . Таким чином, висота дерева дорівнює 3 . На рис. б), в) зображені відповідно збалансоване й незбалансоване цілочислові дерева пошуку.

90