
Зубенко, Омельчук - Програмування. Поглиблений курс
.pdf
Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
P,S0,Sfin,τ0 , де P − певна процедура над простором Π, S0 S та
Sfin S |
– виділені підмножини відповідно вхідних і вихідних станів, |
τ0 Γ – |
початковий момент часу. Результативним назвемо обчис- |
лення p у процедурі P , що розпочинається в момент часу τ0 із пев- ного початкового стану pτ0 = s0 S0 , закінчується у вихідному стані, а всі його проміжні стани невихідні. Для результативного обчислення p на інтервалі [τ0,τ] останній його стан pτ називається заключним і
є результатом. Результат позначається P* (s0 ) і є єдиним, якщо фу-
нкція керування однозначна. У деяких випадках за результат обчис- лення береться не сам заключний стан, а значення на ньому певного результуючого часткового відображення Val : Sfin → B . Також вва-
жають заключними ті скінченні обчислення, на останніх станах яких не визначена функція керування.
Якщо в результативному обчисленні зняти умову, щоб усі проміжні стани були невихідними, то таке обчислення називатимемо гіперре- зультативним. Його вихідні стани можуть зустрічатися й серед про-
міжних, а результат позначається P** (s0 ).
Якщо для певного обчислення значення результуючого відобра- ження Val на заключному стані не визначене, то воно вважається безрезультатним. Безрезультатними є зазвичай нескінченні, а та- кож ті скінченні обчислення, що не мають жодного результативного продовження.
Ми уточнили поняття процедури й обчислення в ній. Це дозволяє уточнити й поняття функції як процедури.
Функціямипроцедурами називаються ініціальні обчислювальні процедури над простором Π .
Після такого уточнення словосполучення "функція-процедура" та "ініціальна обчислювальна процедура" стають синонімами.
З кожною функцією-процедурою P(S0,Sfin,τ0 ) пов'язані два її гра- фіки відповідності на вхідних станах P* :S0 →S fin та P** :S0 →S fin , значення яких на початковому стані s0 S0 складають результати всіх результативних і гіперрезультативних обчислень із початком у момент τ0 на s0 . Про графіки P* та P** кажуть, що їх подає, або об-
числює, функція P .
61

ПРОГРАМУВАННЯ
Багато прикладів функцій-процедур можна знайти в математиці, зо- крема в алгебрі й геометрії. Наприклад, задачі з планіметрії на побудову за допомогою циркуля й лінійки є фактично задачами на побудову пев- них функцій. Станами тут є сукупності фігур на площині, які можуть бути побудовані за допомогою циркуля й лінійки та операцій виділення довільної точки площини, точок перетину фігур, операцій іменування точок і фігур, а також умовних варіантів подібних операцій. Часовий простір тут дискретний і збігається з натуральними числами. Цікава си- туація виникає у випадку існування кількох розв'язків задачі. Розв'язок може забезпечити недетермінована функція, але її можна детермінізу- вати. Якщо, наприклад, для розв'язку задачі певний Виконавець вико- ристовує дошку й необхідно побудувати два різні розв'язки, то після по- будови першого дошка зазвичай витирається і функція повертається в один із попередніх станів, але не в попередню конфігурацію – момент часу інший! Завдяки цьому процес обчислення може бути продовжений детерміновано, як того вимагає побудова другого розв'язку.
Функції-процедури, керування діями в яких реально залежить від часової компоненти, будемо називати темпоральними на відміну від автоматних, коли таке керування не залежить від часу. Класичними прикладами автоматних процедур є скінченні й магазинні автомати (див. підрозд. 1.4.4), машини Тьюрінга (підрозд. 2.1.4), деякі ігрові чис- лення тощо. Для останніх часові фактори можуть відігравати важливу роль, і тоді вони набувають ознак темпоральних процедур. У багатьох іграх важливою є черговість ходу. У грі в шахи (шашки), наприклад, у всі непарні моменти часу ходять білі, а в парні – чорні. Однак є й інші принципові обставини, пов'язані з часом – рокіровка короля залежить від того, чи рухався він до цього моменту. У деяких моделях на страте- гію вибору чергового ходу може впливати обмеженість часу (гра в цейт- ноті). У такому випадку з часом пов'язують певну міру.
Звернемось до натуральної арифметики й розглянемо обчислюва- льну процедуру GCD для знаходження найбільшого спільного дільни-
ка НСД(a,b) двох натуральних чисел.
Приклад 1.10 (алгоритм Евкліда). Нехай Π = Γ,S |
– обчислюваль- |
|||||
ний |
простір |
із |
натуральним часом |
Γ = N , |
множиною станів |
|
S = N + ×N + , N + |
= N \{0}. Набір операцій |
= {α,β} |
і функцію керуван- |
|||
ня δ |
визначимо |
так. Для будь-яких |
a,b N + , |
τ ≥ 0 покладемо: |
||
α(a,b) = (a −b,b),β(a,b) = (a,b −a), δ(τ,(a,b))= (a ≠ b → (a > b → α|β)).
62

|
|
Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ |
|||
Розглянемо |
функцію GCD = Π, |
,δ та її |
ініціалізований |
варіант |
|
GCD (S0,Sfin,0) |
із |
результуючою |
операцією |
проектування |
pr1 , де |
S0 = N + ×N + , Sfin |
= iN . Нескладно перевірити, що повне обчислення |
||||
функції GCD на будь-якому початковому стані s0 = (a,b) є результа- тивним. Дійсно, безпосередньо з означення GCD і співвідношень:
1)gcd(d,d)= d ,
2)(b > a gcd(a,b)= gcd(a,b −a)),
3)(b < a gcd(a,b)= gcd(b,a −b))
випливає, що останній стан у обчисленні функції GCD із початковим станом s0 = (a,b) матиме вигляд (d,d) для деякого числа d = gcd(a,b),
тому що рано чи пізно компоненти чергового стану стануть рівними, а операції α та β не змінюють найбільший спільний дільник компо-
нентів стану. Кінцевий результат обчислення формує операція проек- тування pr1 (d,d)= d . Таким чином, GCD*(a,b) = gcd(a,b) ■
Окремого розгляду заслуговують функції, що закінчують обчислення винятково за часовими критеріями. У цьому випадку можуть навіть не фіксуватись заключні стани, а замість них на станах вводиться, напри- клад, певний частковий порядок, і за результат обчислення (у тому числі й нескінченного) береться найменша верхня грань його станів.
Інший варіант становлять функції, що закінчують обчислення в певний момент часу τ або після деякого моменту τ тощо.
Функції P та Q називаються еквівалентними ( P ≡ Q ), якщо відпо-
відності P * та Q* , які вони обчислюють, еквівалентні. Стан функції P(S0,Sfin,τ0 ) назвемо припустимим, якщо він зустрічається серед станів деякого її результативного обчислення. Покладемо Sacc S – підмножину всіх припустимих станів процедури P . Для графіків фу- нкцій стани за межами підмножини Sacc зайві. Нехай P ′(S0′ ,S′fin ,τ0 ) –
ініціальна функція над простором Π′ із множиною станів Sacc і об-
меженими на Π′ елементарними операціями, функцією переходу та вхідними й вихідними станами процедури P . Очевидно, що функції P та P ′ еквівалентні. Функція, усі стани якої припустимі, називаєть- ся зведеною. Наприклад, наведена вище функція GCD є зведеною.
63

ПРОГРАМУВАННЯ
Має місце така теорема.
Теорема 1.3. Клас графіків функцій-процедур замкнений відносно усіх регулярних композицій.
Доведення – див. вправу 34 ■
Увага! Надалі в тексті слово "функція" буде вживатися в обох смис- лах – і в традиційному теоретико-множинному, і як обчислювальна про- цедура. Яке з них мається на увазі – буде видно з контексту. Наприклад, у розд. 3 функції – це С- та С++-функції, а у формулі O(log2 n) log2 n –
це традиційна логарифмічна функція-відображення ►
* Література для CР: функції-процедури – [1, 51, 65, 77, 80, 129]; рівняння в алгебрі відношень – [52]; обчислювальні процедури – [42, 44, 45, 85]; ігрові числення – [1, 100, 126].
Контрольні запитання та вправи
1.Що таке функція як процедура на змістовному рівні?
2.Пояснити різницю між функцією як процедурою і як відпо- відністю.
3.Що таке графік функції-процедури?
4.Яка різниця між ін'єкцією й сюр'єкцією?
5.Що таке бієкція?
6.Яка роль графіків у поданні функцій?
7.Перерахувати традиційні способи подання функцій. У чому їхні переваги й недоліки?
8.Дати визначення всіх регулярних композицій: а) для унарних функцій; б) для n -арних функцій.
9.Що таке регулярна: а) функція; б) n -арна операція?
10. Довести регулярність функцій над арифметичним базисом:
а) max (x,y); |
б) min(x,y); |
в) max (x +y + z,xyz ); |
г) max2 (x +y + z /2,xyz )+1. При |
цьому: 1) дозволяються |
|
базові предикати-порівняння; 2) базові предикати відсутні, але є базова функція sign(x); 3) те саме, що й у 2), але
sign(x) замінити на |x |. У 2)-3) використовується лише
композиція суперпозиції.
11. Поле шахової дошки визначається парою натуральних чисел, кожне з яких не перевищує вісім: перше число – номер вер- тикалі (при підрахунку зліва направо), друге – номер горизо-
64
Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
нталі (при підрахунку знизу вгору). Дано натуральні числа 1 ≤ k,l,m,n ≤ 8 . Потрібно з'ясувати:
а) чи є поля (k,l ) і (m,n) одного кольору;
б) чи загрожує ферзь на полі (k,l ) полю (m,n); в) чи загрожує кінь на полі (k,l ) полю (m,n).
Розв'язок |
оформити у вигляді регулярних функцій |
f (k,l,m,n) |
над арифметичним базисом (як ходять фігури, |
див. у підрозд. 2.1.4).
12 * . З'ясувати, чи містить десяткове подання числа n вхо- дження цифри 3. Знайти кількість таких входжень. Розв'язок оформити у вигляді регулярних предиката й функції над арифметичним базисом.
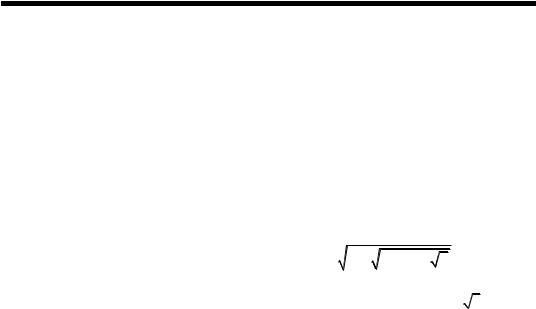
13 * . Довести, що функція f (n) = |
2 + |
2 +... + 2 |
|
є регуляр- |
|||||||||
|
|
|
|
|
144424443 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
ною в дійсній арифметиці, доповненій операцією |
. |
|
|
|
|||||||||
14. Довести: а) регулярність степеневої функції an |
у натураль- |
||||||||||||
ній арифметиці; б) * будь-який регулярний терм для функції |
|||||||||||||
an є циклічним, тобто містить ітерацію або повторення. |
|
|
|||||||||||
15 ** . Композиція мінімізації μ n -арній функції |
f (x ,...,x |
n |
) |
||||||||||
|
|
|
|
|
|
(n −1)-арну |
|
1 |
|
|
|||
ставить |
у |
відповідність |
|
|
функцію |
||||||||
g(x1,...,xn −1) = μ(f (x1,...,xn ) = 0), яка |
повертає |
|
найменше |
||||||||||
значення |
a таке, що f (x1,...,xn −1,a) = 0 , і при цьому всі |
||||||||||||
|
f (x1,...,xn −1,i) для i = |
|
визначені. Базови- |
||||||||||
значення |
0,a −1 |
||||||||||||
ми називаються функції-проекції по i -му компоненту |
prn , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
n > 0 , |
i = |
|
, |
тотожний |
нуль |
0(x) = 0 |
і |
функція |
|||||
1,n |
|||||||||||||
s(x) = x +1. Функція називається частково-рекурсивною,
якщо вона належить замиканню множини базових функцій відносно композицій суперпозиції, примітивної рекурсії (див. підрозд. 2.6.2) і мінімізації. Показати, що будь-яка ча- стково-рекурсивна функція є регулярною n -арною операці- єю над базисом, що включає всі наведені вище базові фун- кції та предикати порівняння "<" і "=" [15, 94].
16 |
* . Довести неперервність відповідностей f |
o f |
2 |
, f |
1 |
f |
2 |
та |
|
1 |
|
|
|
|
f * за кожним з аргументів.
65

ПРОГРАМУВАННЯ
17.Що таке обчислювальний простір?
18.Що таке процес у обчислювальному просторі?
19.Що означає: сукупність процесів подає функцію?
20.Дати означення обчислювальної процедури й обчислення за нею.
21.Яка роль функції керування в обчислювальній процедурі?
22.Що таке обчислення й гіперобчислення?
23.Що таке детермінована й недетермінована функції?
24.Що таке зведена функція-процедура?
25.Що означає: дана процедура обчислює певну відповідність на станах?
26.Побудувати функцію для поділу відрізка навпіл за допомо- гою циркуля й лінійки. У цій і зад. 23-26 для нотації функ- цій використовувати українську мову.
27.Побудувати функцію для знаходження найбільшої спільної мі- ри двох сумірних відрізків за допомогою циркуля й лінійки.
28.Написати функцію для побудови кола за трьома його точ- ками за допомогою циркуля й лінійки.
29.Написати функцію для переправи через річку вовка, кози й капусти. Припустимими операціями є переправа одного з них з одного берега на інший. При цьому на березі не пови- нні залишатися вовк із козою чи коза з капустою.
30.Нехай x – числова змінна і припустимими є операції мно- ження з можливим іменуванням результату й зупинки stop .
Яке значення обчислює така послідовність операцій: а) знайти значення x * x і позначити його x2 ;
б) знайти значення x2 * x2 і позначити його x4 ; в) знайти значення x2 * x4 і позначити його x6 ; г) зупинитись: значення x6 – результат?
Написати функцію для даного обчислення.
31. Написати функції для обчислення значень степенів. Припу- стимі операції – ті самі, що й у вправі 23. Дію "знайти зна- чення a і позначити його v " будемо формально записувати як v ← a . Бажана послідовність операцій із мінімальною кі- лькістю множень:
а) x10 ; |
д) a5 та a19 ; |
з) a4 та a20 ; |
к) a28 . |
б) x12 ; |
е) a15 ; |
и) a5 та a13 ; |
|
в) x16 ; |
є) a21 ; |
і) a2 , a5 , a17 ; |
|
г) x32 ; |
ж) a64 ; |
й) a4 , a12 , a28 ; |
|
66

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
32. Сформулюємо поняття копії та реалізації функцій. Нехай Π1 = Γ,S1 і Π2 = Γ,S2 – довільні обчислювальні простори,
P1 = Π1, 1,δ1 та P2 = Π2, 2,δ2 – довільні процедури від- повідно над Π1 та Π2 , ϕ : S1 → S2 – певне відображення (фу-
нкції кодування). Кажуть, що функція P2 є ϕ-копією (просто копією) функції P1 , а функція P1 – ϕ-реалізацією процедури P2 (просто реалізацією), якщо для будь-якого стану s S1 і
часової константи τ Γ виконується умова: (*) для будь-якого елементарного перетворення f δ1(τ,s) у сукупності δ2(τ,ϕs)
є таке перетворення g , що ϕf (s) = g(ϕs) . Функція P2 назива- ється дублікатом функції P1 , якщо вона є ϕ-копією P1 для певного бієктивного відображення ϕ.
Показати: 1) для кожного обчислення(τ0,s0 ) P1 (τn ,sn ) процедури P1 в її ϕ-копії P2 існує обчислення вигляду
(τ0,ϕs0 ) P2 (τn ,ϕsn ) ; 2) * переходячи від окремих станів до
фактор-класів за ядерною еквівалентністю функцій коду- вання, будь-яку наближену реалізацію певної функції мо- жна стандартним чином перетворити на її дублікат.
33 ** . Нехай Σ* – вільна півгрупа над алфавітом Σ. Покладемо
(Σ) сукупність усіх операцій |
|
appa (u) = app(a,u) , |
a Σ . |
|||||||||||||
Функції над простором Π = |
Γ,Σ* |
із сукупністю елементар- |
||||||||||||||
них операцій (Σ) називаються вільними. Показати, що для |
||||||||||||||||
будь-якої функції існує її вільна реалізація [42]. |
|
|
|
|
|
|
||||||||||
34 ** . Дано довільні функції P (S |
0 |
,S ,τ |
0 |
) |
та |
P (S ,S |
2 |
,τ |
0 |
) |
над |
|||||
|
1 |
|
|
1 |
|
|
|
2 |
1 |
|
|
|
||||
простором Π і предикати p1 та |
p2 на множині станів S . |
|||||||||||||||
Побудувати функції з графіками: 1) |
P *P |
* |
, 2) |
(p → P * |P * ); |
||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
2 |
||
3) (p → P * ); 4) |
{ p → P * } ; 5) (p → P * || p |
2 |
→ P * ) [42]. |
|
|
|||||||||||
1 |
1 |
1 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
||
35 ** . Ввести на станах певний частковий порядок і за резуль- тат обчислення (у тому числі й нескінченного) узяти най- меншу верхню грань його станів. Розглянути теорему про замкненість для отриманих функцій-процедур.
67

ПРОГРАМУВАННЯ
1.4. Алгебричні системи
¾Поняття алгебричної системи
¾Моделі систем
¾Багатосортні Ω - системи
¾Деякі прикладні багатосортні Ω - системи
Ключові слова: алгебричні системи, алгебра, замкнена підмножина, підси- стема, твірна множина, похідні операція та предикат системи, методом ізоморфізм, автоморфізм, гомоморфізм, функція коду- вання, наближена, сильна й точна моделі системи, еквівалентні моделі, ядерна
еквівалентність, конгруенція, фактор-система, типізована операція, багато- сортна Ω -система, вільна Ω -система, Ω -алгебра слів, лексикографічний по- рядок, регулярна Ω-система мов, регулярний вираз, регулярна мова, системи алгоритмічних алгебр, матриці, матрична алгебра, список, лінійний список, стек, черга, орієнтований та неорієнтований графи, зважений граф, мульти- граф, мережа, бінарне дерево, дерево пошуку, збалансоване дерево пошуку, ре- гулярний вираз, скінченний X -автомат, КВ- та РКВ-граматики, контекстно-
вільна мова, дерево виведення, LL (k )-граматика, автомат із магазинною па- м'яттю (МП-автомат), розширена БНФ, синтаксична діаграма.
Алгебричні системи й багатосортні Ω -системи є центральними по- няттями першого розділу. Вони уточнюють інтерпретації ПЧП і дозво- ляють розглянути деякі загальні їхні властивості.
1.4.1. ПОНЯТТЯ АЛГЕБРИЧНОЇ СИСТЕМИ
Нехай A – довільна множина. Нагадаємо, що n -арною операцією на А (m -арним предикатом на А) називається відображення вигля-
ду F : An → A (предикат вигляду P : Am → Bool ). Якщо DF An
( DP Am ), то операція (предикат) називається частковою (частко- вим). Число n (m ) визначає тип операції (предиката). Щоб підкресли-
ти тип операції, будемо писати Fn . Результат операції Fn на векторі (a1,....,an ) позначається термами F (a1,....,an ), (a1,....,an )F , а у випа- дку унарної операції – термами Fa , aF .
68

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
0 -арні операції на A називаються константами. Область визна-
чення константи становить порожній вектор ε : F 0 ε = a для певного виділеного елемента a A .
Алгебричною системою називається трійка A = (A;ΩF ;ΩP ), де A –
носій системи, ΩF = {F1n1 ,F2n2 ,…} – сукупність основних операцій,
ΩP = {P1m1 ,P2m2 ,K}– сукупність основних предикатів на A .
Ураховуючи, що тип Bool є стандартною частиною кожної алгебрич- ної системи, його опускають при визначенні систем. Типом τ алгебрич-
ної системи називається пара τ = (n1,n2,K;m1,m2,K), утворена з типів її
основних операцій і предикатів. Алгебрична система називається: 1) ал-
геброю, якщо ΩP = ; 2) реляційною системою, якщо ΩF = . Алгебра й реляційні системи подаються у вигляді відповідних пар.
Згадувана натуральна арифметика = (N ,Bool;+,−,×,/,0,1;=,<) є ал- гебричною системою типу (2,2,2,2,0,0;2,2). Cистема опуклих замкне- них багатокутників A = (V ;∩) є алгеброю типу 2, а система кругів B = (C; ) – реляційною системою типу 2. Одним із найпростіших кла-
сів алгебр є півгрупи. Вони мають тип 2. Сигнатура їх складається з єдиної асоціативної бінарної операції – множення. Півгрупами є на- туральні числа відносно операцій додавання та множення, слова в певному алфавіті з операцією конкатенації.
Кожну алгебричну систему A можна подати у вигляді певної реля-
ційної системи A% , якщо операції замінити предикатами, що відповіда- ють їхнім графікам. Наприклад, натуральну арифметику подає реля-
ційна система N% = (N;P12,P12,P12,P12,P51,P61;=,<), де P12 (x,y) z (x +y = z),
P51 (x ) x = 0(x ) тощо.
Підсистеми. Зупинимось тепер на важливому в практичному сен- сі питанні: яка мінімальна інформація є необхідною й достатньою для опису носія алгебри? Непорожня підмножина B A системи
A = (A;ΩF ;ΩP ) називається замкненою в A , якщо вона замкнена від-
носно кожної основної операції системи, тобто якщо результат кожної такої операції на елементах із B теж належить A . Система
B = (B;Ω′F ;Ω′P ), де Ω′F і Ω′P – сукупності основних операцій і предика- тів системи A , обмежених на замкнену підмножину B , називається
69
ПРОГРАМУВАННЯ
підсистемою системи A . Щоб не ускладнювати позначення, будемо там, де це можливо, сукупності основних операцій і предикатів під- систем і систем позначати однаково – ΩF та ΩP , відповідно. Якщо A
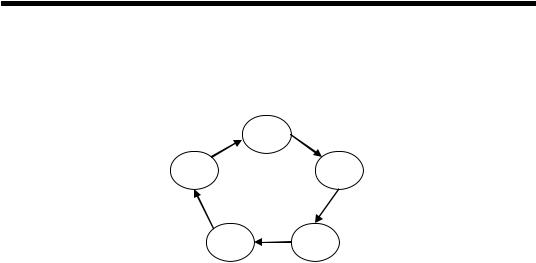
є алгеброю, то в цьому випадку говорять про підалгебру алгебри A . Алгебра A5 = ({a1,a2,a4,a3,a5};λ), де операція λ задана графом
|
a1 |
|
a5 |
|
a 2 |
a 4 |
a3 |
, |
|
|
не має власних підалгебр, тобто таких, що не збігаються із самою ал- геброю, а алгебра N + = ({1,2,...};+) має зліченну кількість власних під- алгебр, наприклад вигляду ({k,k +1,...};+), k >1.
Сукупність непорожніх власних підсистем даної системи має важливу властивість – вона замкнена відносно перетину систем (вправа 2.7). Перетин усіх непорожніх власних підсистем системи A є найменшою (головною) підсистемою A . Якщо взяти арифметику ці-
лих чисел Z10 , то головною її підсистемою є {0}, а алгебра N + = ({1,2,...};+) не має головної підалгебри.
Нехай B – довільна підмножина системи A . Серед підсистем A обов'язково є й надсистеми B (напр., сама система A ). Нехай – сукупність усіх підсистем системи A , що включають B . Тоді пере-
тин B* усіх систем із є найменшою підсистемою A , що містить усі елементи B . Система B* = (B*;ΩF ;ΩP ) називається підсистемою
системи A , породженою множиною B , множина B* – замкненням множини B відносно операцій із ΩF , а елементи множини B – твір-
ними елементами замкнення B .
Якщо B* = A , то множина B називається множиною твірних сис- теми A . Система може мати не одну множину твірних. Наприклад, в алгебрі A5 кожен елемент ai сам є твірним алгебри. Якщо в алгебрі
A5 вибрати за твірний елемент a1 , то решту її елементів можна зада- ти термами a2 = λ(a1), a3 = λ(λ(a1)), a4 = λ(λ(λ(a1 ))), a5 = λ(λ(λ(λ(a1)))).
70
