
Зубенко, Омельчук - Програмування. Поглиблений курс
.pdf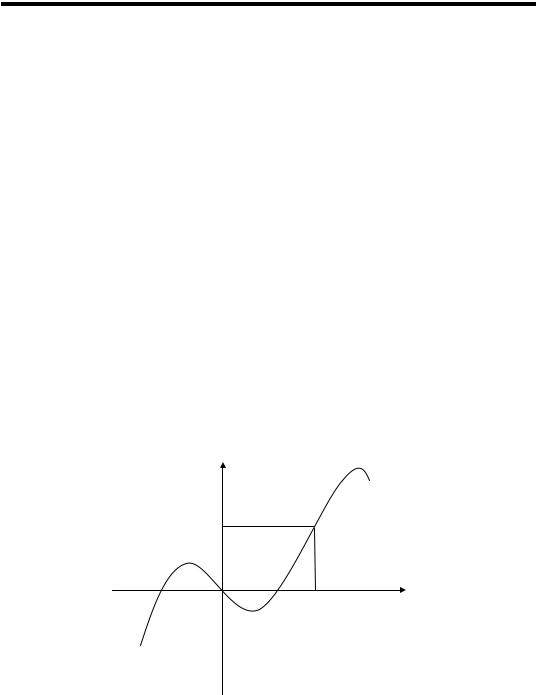
Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
технічних засобів. Досить пригадати відомі ще зі школи таблиці Брадіса для обчислення елементарних функцій – степенів, коренів, десяткових логарифмів, тригонометричних функцій тощо. Таблиці широко викорис- товуються в обчислювальній математиці й програмуванні, наприклад при так званій інтерполяції функцій, яка дозволяє за відомими таблич- ними значеннями функцій у певних фіксованих точках наближено об- числювати їхні значення на довільних аргументах. Моделі таблиць є ос- новним засобом для організації та збереження інформації в пам'яті ЕОМ.
Інший відомий спосіб подання відображень – геометричний. Він полягає в розташуванні за певним правилом (масштабом) усіх елеме- нтів областей визначення та значень на двох перпендикулярних пря- мих, які перетинаються в точці O і називаються осями абсцис (вісь OX ) і ординат (вісь OY ). При цьому аргументи розташовуються на
першій осі, а результати – на другій. Тоді кожній парі (x,αx ) відо-
браження α відповідає точка на квадратній площині, якій належать осі OX та OY (рис. 1.3).
Геометричний спосіб використовується для наближеного подання й обчислення значень функцій. Він зручний при вивченні інтегральних властивостей функцій, таких як монотонність, опуклість тощо.
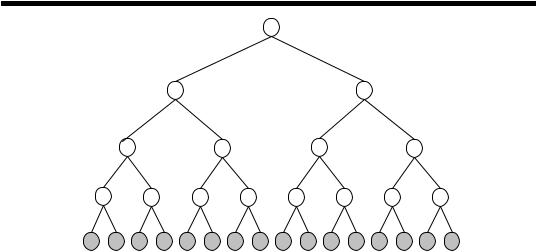
Для подання функцій можуть застосовуватись і графи, зокрема де- рева (див. підрозд. 1.4.4). Такий спосіб називається графічним. Типо- вим прикладом є кодові дерева, які за двійковим кодом дозволяють знайти відповідний символ кодової таблиці, графи скінченних авто- матів тощо. На рис. 1.4 зображено кодове дерево для двійкових кодів шістнадцяткових цифр.
Y
αx
O |
x |
X |
Рис. 1.3
51
ПРОГРАМУВАННЯ
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
1 |
|
|
0 |
1 |
0 |
1 |
|
0 |
1 |
|
|
0 |
|
1 |
0 |
1 0 |
1 0 |
1 0 |
1 0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 1 2 3 4 5 6 7 8 9 A B C D E F
Рис. 1.4
Зазначимо, що конкретні табличні, геометричні й графічні специфікації відображень тим цікавіші на практиці, чим ефективніше вони алгоритмізуються. Наприклад, щоб знайти значення табличного відображення для даного аргументу, достатньо простим перебиранням знайти в таблиці стовпчик із даним аргументом і взяти другий його компонент. Однак якщо рядків багато, то це може бути не дуже зручно. У таких випадках пошук можна зробити більш прийнятним, якщо аргументи в таблиці розташувати в певному лінійному порядку (див. підрозд. 4.1.2).
1.3.3. АЛГЕБРИЧНІ СПЕЦИФІКАЦІЇ
Універсальним і потужним засобом подання відображень є алгеб- ричний. Розрізняють явні й неявні алгебричні специфікації. В явних відображення подають як конструктивні об'єкти. Для цього фіксують певні сукупності атомних (базових) відображень і конструкторів на відображеннях (композицій), що дозволяють будувати з базових відо- бражень складніші. Наприклад, композиція суперпозиції дозволяє бу- дувати складні тригонометричні функції на основі базових тригоно- метричних функцій і арифметичних операцій. Нові функції подають- ся за допомогою спеціальних термів – алгебричних виразів.
Розглянемо певний набір класичних композицій, що найчастіше вжи- ваються для явної специфікації відображень. Вони цікаві тим, що збері- гають процедурність аргументів, тобто якщо їх застосувати до графіків
52

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
не просто відображень, а функцій, то в результаті будуть отримані теж графіки певних функцій. Спочатку розглянемо композиції унарних відо-
бражень. Композицією рангу 1 над множиною A будемо називати будь-
яку операцію вигляду K : A ×...× A × (A →A) ×...×(A →A) → (A →A). Звичайні n -арні операції на A належать до композицій рангу 0. Дві композиції
рангу 1 уже зустрічалися вище – множення ( o) та обернення ( −1 )17.
Зазначимо, що результат обернення є відображенням тільки для сюр'єктивних відображень. Нехай p – предикат на A ,
α : A → A ,β : A → B , γ : A → C – довільні відображення.
Обмеженням відображення β |
за предикатом p називається відо- |
|
|
def |
|
браження |
β ↓p = β ∩ p(A)×B . |
Якщо p(a) =1, то результатом обме- |
ження β ↓p |
на елементі a буде значення βa , якщо ж p(a) = 0 , то зна- |
|
чення не визначене.
Розгалуженням за предикатом p відображень β, γ називається |
ві- |
|
дображення (p → β|γ) = β ↓p γ ↓¬p . |
Таким чином, якщо p(a) =1, |
то |
результатом розгалуження (p → β|γ) |
на елементі a буде значення βa , |
|
якщо ж p(a) = 0 , то значення γa . |
|
|
Обходом за предикатом p відображення β називається відобра- ження (p → β) = β ↓p i¬p . За межами області істинності предиката p обхід (p → β) діє як одиничне відображення.
Звуженням відображення β за предикатом p на B називається відображення β ↑p : A → B таке, що β ↑p = β I A × p(B) .
Позначимо через αp* замикання відображення α відносно преди-
ката p на A , тобто αp* = ((α ↓p ) ↑p )* .
Ітерацією за предикатом p відображення α називається відобра-
def
ження { p → α} = ((αp )* oα) ↑¬p . За означенням { p → α}(a) = b , якщо
існує m ≥ 0 , за якого послідовність b0 = a, bi = f (bi −1) , i =1,m , є такою,
m −1
що bm = b і виконується умова & p (bi )& ¬p (b).
i =0
17 Обернення не зберігає процедурність.
53
ПРОГРАМУВАННЯ
Приклад 1.8. Функція Gcd = {q → (p → α|β)}opr1 обчислює найбі- льший спільний дільник двох натуральних чисел, де α(n,m) = (n −m,m) ,
β(n,m) = (n,m −n), p(n,m) = m < n та q(n,m) = n ≠ m для всіх n,m N .
Про коректність функції Gcd див. прикл. 1.10 ■
Повторенням за предикатом p відображення α називається відо-
def
браження [p → α] = α{ p → α} .
Недетермінованим вибором відображень α1,...,αn : A → A за пре-
дикатами |
|
p1,..., pn називається відповідність (p1 → α1 || … |
|||
|| pn → αn ) |
def |
n |
|
αi ↓p . |
|
|
= |
U |
|
||
|
|
|
i =1 |
i |
|
|
|
|
|
||
Предикат |
pi |
іноді називають охороною відображення αi . Якщо |
|||
охорони p1,..., pn |
|
попарно не перетинаються, то результат недетермі- |
|||
нованого вибору (p1 → β1 || … || pn → βn ) буде теж відображенням.
Приклад 1.9. Нехай sign(x ) = (x < 0 → −1||x = 0 → 0||x > 0 →1) та
± x = (x > 0 → x || x>0 → − x ). Тоді перший вибір є відображенням,
а другий – ні ■
Нехай p1,..., pn – довільні охорони, деякі з яких виділені як заклю- чні. Детермінованим вибором відображень α1,...,αn : A → A за охоро- нами p1,..., pn називається відображення
(p1 → α1 | … | pn → αn ) |
def |
n i −1 |
¬pk (a)& pi (a )→ γi |#) , |
= |
( & |
||
|
|
i =1 k =1 |
|
де γi = αi , якщо охорона pi є заключною, і γi = αi ...αn , якщо ні. Якщо
всі умови на певному елементі одночасно хибні, то значення вибору на ньому не визначене.
Наведені композиції разом із множенням і логічними зв'язками на- зиваються регулярними18. Як уже зазначалось, вони зберігають фун- кціональність аргументів. Функції, що отримують за їхньою допомо- гою, теж називаються регулярними. Процедури обчислення значень регулярних функцій формулюються досить просто. Наприклад, щоб знайти результат добутку fg на елементі a , достатньо за правилом g
знайти результат g(a) і до нього застосувати правило функції f . Щоб
18 Обернення не є регулярною композицією
54

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
знайти результат b ітерації {p → f } на елементі a , необхідно спочатку перевірити предикат p на a . Якщо він виконується, то необхідно об- числити за правилом f значення a1 = fa , у протилежному випадку покласти b = a ; потім перевірити предикат p на a1 . Якщо він вико- нується, то необхідно обчислити за правилом f значення a2 = fa1 , у протилежному випадку покласти b = a1 тощо. Даний процес побудо- ви послідовності a0 = a , a1 = fa0 , a2 = fa1 ,… або завершиться на яко- мусь n -му кроці, n ≥ 0 , з результатом b = an , або буде продовжуватись
до нескінченності з беззмістовним результатом. Аналогічно формулю- ються правила й для решти композицій.
Нехай A – довільна множина. Відображення вигляду An → A на- зиваються n -арними операціями. Визначимо регулярну алгебру n -арних операцій.
Нехай α = (i1,i2,...,in ) – довільна перестановка чисел (1,2,...,n). Компо- зиція перестановки аргументів довільній операції f : An → A ставить у
відповідність операцію f α : An → A таку, що f α(a ,...,a ) = f (a ,...,a ). |
||||||||
|
|
|
|
1 |
n |
i |
i |
|
Композиція ототожнення |
аргументів |
|
|
|
1 |
n |
||
|
|
довільній |
|
операції |
||||
f : An → A ставить у відповідність операцію f τ : An → A таку, що |
||||||||
f τ(a ,a |
2, |
...,a |
) = f (a ,a ...,a |
n |
) . |
|
|
|
1 |
n |
1 1 |
|
|
|
|
||
Композиція параметризації аргументів параметру a A й операції f : An → A ставить у відповідність операцію fa : An −1 → A таку, що
fa (a2,...,an ) = f (a,a2,,...,an ). |
|
|||||
Композиція введення |
фіктивних аргументів |
довільній операції |
||||
f : An → A ставить у відповідність операцію f φ : An +1 → A таку, що |
||||||
f φ(a ,a |
2 |
...,a ,a |
) = f (a |
2 |
,...,a |
). |
1 |
n n +1 |
|
n +1 |
|
||
Композиція підстановки (суперпозиції) операції |
f : Am →A й операці- |
|||||
ям g1,...,gm : An → A ставить у відповідність операцію
S(f ,g1,...,gm ): An → A :S(f ,g1,...,gm )(a1,...,an ) = f (g1(a1,...,an ),...,gm (a1,...,an )).
Нехай prn : An |
→ A , |
1 ≤ i ≤ n |
– функція проектування за i -м ком- |
|||||
i |
|
|
|
|
|
|
|
|
понентом, тобто prn (a ,...,a ) = a |
i |
для < a ,...,a |
n |
> An . |
Підстановку |
|||
S (g,g1, prn2..., prnm ) |
i 1 |
n |
|
1 |
|
|
||
умовимось позначати коротко: S(g,g1). |
|
|||||||
55

ПРОГРАМУВАННЯ
Позначимо через |
fB* замикання операції |
f |
: An → A |
за першим |
|||||||||||
|
|
|
|
|
|
|
B A , тобто fB* = |
∞ |
|
|
|||||
компонентом відносно підмножини |
U f n , де |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n =0 |
|
|
f 0 = En +1 = {(< a,a |
2 |
,...,a |
n |
>,b) An × A : a = b} , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f n (a ,...,a |
n |
) = f ↓ |
B×A |
n −1 (f n −1(a ,...,a ),a |
2 |
...,a ), |
n > 0 . |
||||||||
1 |
|
|
|
|
|
1 |
n |
|
n |
|
|
|
|||
Композиція ітерації предикату |
p на |
An |
та операції |
|
f : An → A |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
* |
¬p(An ) |
|
|
ставить у відповідність операцію {p → f }= ((f p(An )) ) ↑ |
|
|
. За озна- |
||||||||||||
ченням { p → f }(a1,...,an ) = b , якщо існує m ≥ 0 , за якого послідовність
b0 = a1, bi |
= f (bi −1,a2,...,an ), i = |
1,m |
, є такою, |
що bm = b і виконується |
m −1 |
p (bi ,a2,...,an )& ¬p (b,a2,...,an ). |
|
||
умова & |
|
|||
i =0 |
|
|
|
|
Композиція повторення предикату p на |
An і операції f : An → A |
|||
ставить у відповідність операцію [p → f ]= S({ p → f }, f ).
Наведені вище композиції n -арних операцій разом із композицією розгалуження й логічними зв'язками називаються регулярними. По- значимо їхню сукупність Ξ0 .
Як і у випадку регулярних композицій унарних відображень, регу- лярні композиції n -арних операцій теж зберігають процедурність ре- зультуючої операції, тобто якщо їхні аргументи є функціями, то до- сить просто сформулювати правило для обчислення й результуючої
операції. Нехай F = {f1..., fn } та P = {p1..., pm } – довільні сукупності
операцій і предикатів на An . Операції, отримані з елементів F UP за допомогою регулярних композицій, називаються регулярними n -арними операціями над базисом F UP .
Регулярні n -арні операції над достатньо простими базисами є уні- версальними алгоритмічними системами (див. вправу 15).
Для подання регулярних операцій використовують регулярні терми у спрощеній префіксній та інфіксній формах. Наприклад, похідну регулярну операцію S(×,2,sin(x)) записують у вигляді
звичайного інфіксного терму 2sin x , операцію [x > 0 →S(ln,x /2)|0] –
як [x > 0 → lnx /2|0] тощо.
Неявні засоби специфікують відображення (відповідності) за до- помогою спеціальних формул ПЧП чи формул числень вищих поряд-
56

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
ків, які описують зв'язок між аргументами й значеннями відображень у певній алгебрі. Такі формули називаються рівняннями або систе- мами рівнянь. Це можуть бути як звичайні рівняння з предметними змінними, так і (що важливіше для застосувань) функціональні, у яких невідомими є не предметні змінні, а функціональні зі значення- ми – відображеннями чи відповідностями. Наприклад, звичайне рів- няння xy =1 із невідомим y визначає відображення-гіперболу, а рів-
няння y2 − x2 =1 відносно y – двозначну відповідність y = ± x2 +1 .
Функціональні рівняння зазвичай мають багато розв'язків. Тому окрім проблеми пошуку розв'язків рівняння існує й додаткова про- блема – вибору необхідного розв'язку.
У теорії найбільш вивчені канонічні функціональні рівняння вигляду f = Φ(f ), де Φ – певна композиція на множині відображень. Напри-
клад, функціональне рівняння f (x )= (x >100 → x −10| f (f (x +11))), де
x пробігає цілі числа, а f – функціональна змінна типу Z → Z , має кіль- ка розв'язків, найменшим серед яких (відносно теоретико-множинного включення) є відображення Fp (x ) = (x >100 → x −10|91), відоме як 91-
ша функція Мак-Картні. Найменшим розв'язком іншого рівняння – f (n ) = (n = 0 →1,n × f (n −1)), де n пробігає натуральні числа, а f – фу-
нкціональна змінна типу N → N , – є функція-факторіал n !.
Як ще один приклад розглянемо канонічну систему рівнянь у
регулярній |
алгебрі відповідностей: |
(*) xi = Ri (x1,...,xn ),i = |
1,n |
, |
де |
Ri (x1,...,xn ) |
– регулярні вирази відносно невідомих відповідностей |
||||
x1,...,xn і, |
можливо, деяких заданих відповідностей, побудовані за |
||||
допомогою |
чотирьох композицій: |
множення o, об'єднання |
|
||
(частковий випадок недетермінованого вибору двох відповідностей
f g = (1 → f ||1 → g)), ітерації * |
за тотожно-істинним предикатом і |
|
суперпозиції. Сукупність B(A × A) усіх відповідностей на множині A є |
||
чумом відносно звичайного |
теоретико-множинного |
включення: |
f1 p f2 xf1y xf2y . Найменшою верхньою гранню |
зростаючого |
|
ланцюга відповідностей є їхнє множинне об'єднання, а нулем –
порожня відповідність ε . Композиції f |
o f |
2 |
, f |
1 |
f |
2 |
та f * |
неперервні |
1 |
|
|
|
|
|
|||
за кожним з аргументів (див. вправу |
|
16). |
|
Ураховуючи, що |
||||
57

ПРОГРАМУВАННЯ
суперпозиція неперервних відображень неперервна, до системи (*) можна застосувати теорему про нерухому точку (див. підрозд. 1.2.5) і отримати таку теорему.
Теорема 1.2. Система рівнянь (*) має найменший розв'язок
∞ |
|
|
∞ |
|
|
|
означенням Ri(0)(x1,...,xn ) = xi , |
||||
( R1(k )(ε,...,ε),..., Rn(k )(ε,...,ε)) |
, |
де за |
|||||||||
k = |
0 |
|
k = |
0 |
|
|
|
|
|
|
|
R(k +1)(x ,...,x |
|
) = R (R(k )(x ,...,x |
|
),...,R(k )(x ,...,x |
|
)) для i = |
|
. |
|||
n |
n |
n |
1,n |
||||||||
i |
1 |
i |
1 1 |
n |
1 |
|
|
|
|||
Наслідок. Розв'язки лінійних функціональних рівнянь з одним
невідомим x вигляду |
x = f o x g та |
x = x o f g є регулярними |
відносно коефіцієнтів f |
і g . |
|
Доведення. З теореми 3.1 випливає, |
що найменший розв'язок x0 |
|
першого рівняння збігається з |
∞ |
|
|
R(k )(ε) , де |
|
||
|
k =0 |
|
|
R(x) = f o x g,R(k )(x) = f k o x f k −1 og ... f og g = |
|||
k −1 |
x0 = |
∞ |
∞ |
= f k o x ( f i og) . Тоді |
f k og = ( f k )og = f * og . |
||
i =0 |
|
k =0 |
k =0 |
Аналогічно для другого рівняння отримуємо найменший розв'язок x0 = g o f * ■
1.3.4. ФУНКЦІЇ ЯК ОБЧИСЛЮВАЛЬНІ ПРОЦЕДУРИ
Повернемось до означення функції та спробуємо його формалізувати. Як випливає з означення, для уточнення поняття функції необхідно (і достатньо) уточнити поняття процедури й обчислення. Розпочнемо з обчислень.
Виберемо майже гранично можливий рівень абстракції (який умовно можна було б назвати пропозиційним): усі об'єкти трактуються як теоретико-множинні чорні скриньки, усередину яких ми не заглядаємо.
Кожне окреме обчислення не є одноразовим актом: розпочавшись у певний фіксований момент часу з певною початковою інформацією на вході, воно розгортається в часовому просторі й супроводжується виконанням певних елементарних дій. Обчислення може бути скінченним або нескінченним у часі, але в обох випадках існує механізм для визначення його результату або визнання беззмістовним. Таким чином, можна констатувати, що
58

Розділ І. ЛОГІКО-АЛГЕБРИЧНІ УНІВЕРСАЛІЇ
обчислювальний простір, в якому розгортаються обчислення, є, як мінімум, двовимірним – із часовою та інформаційною координатами.
Нехай |
< Γ,< > – |
довільна лінійно впорядкована сукупність, |
яку |
будемо |
трактувати |
як часовий простір19. Позначимо τ+ та |
τ− |
безпосередньо наступний і попередній моменти часу відносно моменту τ . Вважається, що в часовому просторі немає найменшого й найбільшого елементів.
Інформаційну складову процесів обчислень подають стани. На да- ному етапі нас не буде цікавити їхня структура. Нехай S – довільна множина станів.
Двійка Π = Γ,S називається обчислювальним простором, а пари (τ,s) Γ ×S – конфігураціями простору.
|
Нехай |
τ,τ1,τ2 Γ . |
Покладемо |
′ |
′ |
+ |
||||
|
Γτ = {τ Γ|τ ≤ τ |
} , Γτ = Γτ \ {τ} , |
||||||||
Γ− = Γ \ Γ , |
[τ ,τ |
] = {τ : τ |
≤ τ ≤ τ |
2 |
} . Абстрактним процесом в обчислю- |
|||||
τ |
τ |
1 2 |
1 |
|
|
|
|
|
|
|
вальному просторі Π із початком у момент часу τ |
називається дові- |
|||||||||
льне відображення вигляду |
p : Γτ → S , |
а абстрактним процесом на |
||||||||
інтервалі |
[τ1,τ2 ] – довільне |
|
|
відображення вигляду |
p : [τ1,τ2 ] → S . |
|||||
Стани pτ ( pτ1 ), |
pς , τ < ς |
( τ1 < ς < τ2 ) та pτ2 називаються початковим, |
||||||||
проміжними й заключним станами процесу p . |
|
|
||||||||
|
Візьмемо довільну функцію f : S →S та її аргумент s . Якщо процес |
|||||||||
p |
розпочинається у стані s і його заключний стан збігається з fs , то |
|||||||||
кажуть, що він подає значення функції |
f на аргументі s . Зафіксуємо |
|||||||||
певний момент часу τ0 як початковий. Сукупність процесів Ξ , що роз- починаються в момент τ0 : 1) подає функцію f , якщо для кожного її ар-
гументу з області визначення ця сукупність містить процес, який подає її значення на даному аргументі; 2) строго подає f , якщо вона подає f
і не містить "зайвих" процесів (тих, що не подають значення f ).
Тепер серед усіх абстрактних процесів у обчислювальному просторі Π виділимо процеси-обчислення та їхні сукупності. Для цього зафік-
суємо певну сукупність ={ fi : S → S | i ≥ 0} елементарних операцій
на станах і визначимо функцію керування процесами. Остання пов'я- зує з кожним моментом часу процесу одне або кілька можливих еле-
19 У деяких випадках часовий простір може мати складнішу структуру.
59

ПРОГРАМУВАННЯ
ментарних перетворень його поточного стану. Покладемо її як таку,
що має вигляд δ : |
Γ ×S → 2 20. |
Нехай Π = Γ,S |
– довільний обчислювальний простір. |
Обчислювальною процедурою над простором Π із сукупністю елементарних перетворень і функцією керування δ називається трійка
P = Π, ,δ .
Кожна обчислювальна процедура породжує певну сукупність обчи- слювальних процесів у просторі Π. Нехай τ Γ та s S – довільні мо- мент часу і стан. Обчислення p : Γτ → S за процедурою P із початком
у момент часу τ і початковим станом |
|
s0 визначається рекурентно: |
||||
pτ = s |
і для всіх ς > τ |
pς = f |
ς |
(pς− ), де f |
ς |
δ(ς, pς− ). Функція керування |
0 |
|
|
|
|
||
за поточним моментом часу ς і станом pς− у попередній момент часу
визначає сукупність елементарних операцій, які можуть бути засто- совані для отримання стану процесу в момент ς . Вважатимемо, що
обчислення p у момент часу ς переходить від попереднього стану
pς− до наступного стану pς і позначатимемо цей факт pς− →P pς .
Варіантів таких переходів може бути кілька, оскільки функція пере- ходу багатозначна. Насправді їх може бути: а) два і більше (у випадку
недетермінованих процедур); б) рівно один (у випадку детермінова-
них процедур); в) жодного (обчислення зупиняється).
Обчислення p за процедурою P на інтервалі [τ1,τ2 ] визначається як обмеження відповідного обчислення p за процедурою P із почат- ком у момент τ1 на часовий інтервал [τ1,τ2 ] . Казатимемо, що обчис- лення p у цьому разі розпочинається станом pτ1 і закінчується ста- ном pτ2 , і позначатимемо цей факт pτ1 P pτ2 .
Зазвичай інтерес становлять не всі можливі обчислення в процеду- рі, а насамперед ті, що розпочинаються в певний фіксований момент часу з певних виділених вхідних станів і закінчуються певними виді- леними вихідними станами. Тому введемо поняття ініціальної обчис- лювальної процедури P(S0,Sfin,τ0 ) над простором Π як четвірки
20 У загальному випадку функція керування може задавати й перетворення часового компонента (при цьому в процесі обчислень можливі стрибки в часовому просторі як уперед, так і назад) [42].
60
