51) Інтегполяційна теорема

Теорема (інтерполяційна теорема). Нехай секвенція _ має виведення. Тоді існує формула  сигнатури ()()() така, що секвенції _  та _  мають виведення. Таку  називають інтерполяційною формулою або інтерполянтом.

52) Семантична і синтаксична визначність, теорема про визначність

Предикатний символ q семантично визначний через предикатні символи {p₁,…, p_n}, де q{p₁,…, p_n}, якщо для кожних {p₁,…, p_n}-тотожних еквітонних моделей істинності A=(M, I_A) та В=(M, I_В) множини формул  маємо q_A  q_В .

Предикатний символ q синтаксично визначний через предикатні символи {p₁,…, p_n} в множині формул , якщо існує формула  із () ={p₁,…, p_n} така, що    q.

Теорема 6. Нехай ПС q синтаксично визначний через {p₁,…, p_n} в множині формул . Тоді q семантично визначний через {p₁,…, p_n}.

Теорема 7. Нехай предикатний символ q семантично визначний через {p₁,…, p_n}. Тоді q синтаксично визначний через {p₁,…, p_n} в множині формул .

53) Квазіарні предикати, їх різновиди. Дуальні предикати, дуальні моделі мови.

Функцію вигляду ^VA{T, F} назвемо V-квазіарним предика­том А

В класі квазіарних предикатів природним чином виділяємо підкласи монотонних (еквітонних) та антитонних предикатів.

Неокласичнасемантика часткових однознач­них предикатів та пересиченасемантика тотальних неоднозначних предикатів дуальні.

АС B = (A, I_B) назвемо дуальною до A = (A, I_A), якщо для ко­жного Ps маємо 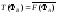та.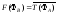

54) Визначення відношень …

1) “Істиннісний” наслідок _A|=_T :

 _A|=_T   T(_A)  T(_A).

2) “Хибнісний” наслідок _A|=_F :

 _A|=_F   F(_A)  F(_A).

3) “Cильний” наслідок _A|=_TF :

 _A|=_TF   T(_A)  T(_A) та F(_A)  F(_A).

4) “Неспростовнісний” наслідок _A|=_Cl :

 _A|=_Cl   T(_A)F(_A) = .

5) “Насичений” наслідок _A|=_Cm :

 _A|=_Cm   F(_A)T(_A) = ^VA.

55) Співвідношення між відношеннями … в різних семантиках.

Нехай B = (A, I_B) дуальна до A = (A, I_A). Тоді:

1)  _A|=_T    _B|=_F  та  _A|=_F    _B|=_T ;

2)  _A|=_Cl    _B|=_Cm  та  _A|=_Cm    _B |= _Cl .

56) Логіки вищих порядків. Теза Гільберта

57) 3-значні логіки Лукасєвича, Кліні. Багатозначні логіки Поста

Ян Лукасевич предложил трёхзначную логику, где возможны три значения: - истинно («да»); - ложно («нет»); - возможно («неопределённо»). К последним, например, относятся ситуации, которые ещё не случились, но могут случиться… 

Кліні:

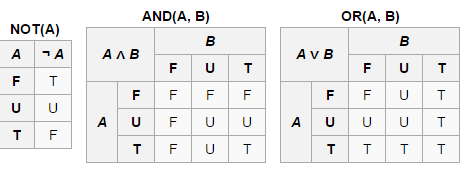
Э. Пост, в отличие от Я. Лукасевича, подошел к построению многозначной логики исключительно формально. Он предложил следующие обозначения: 1 – истина, 0 – ложь, все же числа, находящиеся в промежутке между этими значениями, обозначают определенную степень истинности.

58) 4-значна логіка Белнапа

59) Мова пропозиційної інтуїціоністьскої логіки, інтуїністьскої логіки 1-го порядку

Розглянемо мову інтуїціоністської пропозиційної логіки (ІПЛ).

Алфавiт мови ІПЛ складається iз символiв логiчних зв’язок , , &, та множини Ps пропозицiйних символів.

Визначення формули мови ІПЛ iндуктивне.

1) кожний АPs є формулою;

2) якщо  та  – формули, то , , &,  – формули.

Множину формул мови ІЛП позначимо Fp.

Розглянемо мову інтуїціоністської логіки предикатів 1-го порядку (ІЛП).

Алфавiт мови ІЛП складається iз таких символів:

– предметнi імена (змiннi) x, y, z,...;

 -предикатнi символи (ПС) p₀, p₁, p₂,... заданої арностi;

- символи логiчних операцiй ,, &,тах,x.

Множину Ps предикатних символів назвемо сигнатурою мови ІЛП.