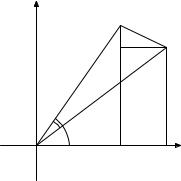
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.4. |
|
приближенных вычислений и тем ближе средняя скорость к sin t. Как говорят, мгновенная скорость проекции конца стрелки в тот момент, когда стрелка прошла расстояние t, равна sin t. Точнее говоря, эта мгновенная скорость равна − sin t, так как при возрастании пройденного расстояния от t до t + τ проекция конца стрелки движется по оси абсцисс в «отрицательном направлении» (от б´ольших чисел к меньшим). Говоря по-ученому, производная от функции y = cos t — это функция y = − sin t.
§ 6. Определение тригонометрических функций
В этом параграфе мы аккуратно сформулируем определения тригонометрических функций.
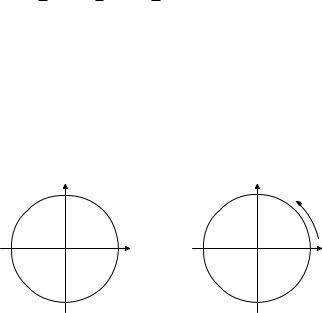
Для этого введем на плоскости прямоугольную систему координат и рассмотрим окружность радиуса 1 с центром в начале координат (рис. 6.1а).
Такой чертеж принято называть тригонометрическим кругом (или тригонометрической окружностью). Точку с координатами (1; 0), лежащую на этой окружности, будем называть началом отсчета или точкой ноль (не путайте с началом координат!). Направление движения против часовой стрелки будем называть положительным направлением (рис. 6.1б).
Тригонометрическая окружность служит для того, чтобы на-
24
носить на нее числа. Это делается так. Пусть у нас есть число t. Начав с начала отсчета, пройдем по тригонометрической окружности путь длиной |t|: если t > 0 — в положительном направлении, если t < 0 — в отрицательном (возможно, нам придется при этом несколько раз пройти по одному и тому же месту). Точка, в которой мы остановились, и есть точка на окружности, соответствующая числу t.
По-другому точку на окружности, соответствующую числу t, можно себе представить как второй конец намотанной на окружность нерастяжимой нити длины |t|, один конец которой закреплен в начале отсчета, или как положение стрелки часов, о которых мы говорили в предыдущем параграфе, в момент t.
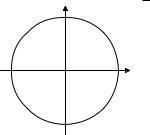
На рис. 6.2 отмечено, какая точка соответствует числу π/2 (длина дуги от 0 до этой точки составляет как раз 1/4 всей длины окружности, т. е. 2π/4 = π/2). Впрочем, в ту же точку попадут и числа π2 + 2π, π2 − 2π, π2 + 4π — при движении по окружности мы сделаем один или несколько лишних кругов, но остановимся все в той же точке.
Задача 6.1. Нанесите на тригонометрический круг числа 3π/2, π/4, −π/4, −π/2, −7π/4, −7π/2. Сколько различных точек у вас получилось?
Задача 6.2. Нанесите на тригонометрическую окружность точки, соответствующие числам πn/2 для всех целых n. Сколько различ-
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
б) |
Рис. 6.1. Тригонометрический круг.
25
|
|
|
|
|
|
|
|
||
|
Рис. 6.2.
ных точек у вас получилось?
Задача 6.3. Выполните задание предыдущей задачи для чисел: а) −π/4 + πn; б) π/3 + 2πn (n — любое целое число).
Задача 6.4. В какой четверти будет находиться точка тригонометрической окружности, соответствующая числу 1000?
Задача 6.5. Сколько точек получится, если нанести на тригонометрический круг все числа вида 73πn/107, где n — целое число?
Задача 6.6. Каким должно быть число a, чтобы среди точек, соответствующих числам вида 2πan при всех целых n, было бы конечное число различных?
Задача 6.7. Пусть числу t соответствует на тригонометрической окружности точка P . Запишите какое-нибудь другое число, которому на тригонометрической окружности соответствуют:
а) та же самая точка P ;
б) точка, симметричная точке P относительно начала координат;
в) точка, симметричная точке P относительно оси абсцисс;
г) точка, симметричная точке P относительно оси ординат;
26
д) точка, симметричная точке P относительно биссектрисы первого и третьего координатных углов.
Задача 6.8. Как выглядит на тригонометрическом круге множество точек, соответствующих числам из промежутков: а) [0; π/2]; б) [π/2; 2π]; в) (−π; π); г) (2; 9).
Если 0 < t < π/2, то число t на круге будет расположено так, что отрезок, соединяющий соответствующую точку с началом координат, составит угол t радиан с осью абсцисс. В самом деле, в этом случае длина дуги от 0 до t будет как раз равна t (рис. 6.3).
Теперь все готово для того, чтобы ввести основные определения тригонометрии.
Рис. 6.3.
Определение. Косинусом числа t называется абсцисса точки на тригонометрическом круге, соответствующей числу t.
Если t — радианная мера острого угла, то косинус этого угла в нашем прежнем смысле равен косинусу числа t в новом смысле.
Косинус числа t обозначается cos t.
Определение. Синусом числа t называется ордината точки на тригонометрическом круге, соответствующей числу t.
Если t — радианная мера острого угла, то синус этого угла в нашем прежнем смысле равен синусу числа t в новом смысле.
Синус числа t обозначается sin t.
Определение. Тангенсом числа t называется отношение синуса числа t к его косинусу.
Если t — радианная мера острого угла, то тангенс этого угла в нашем прежнем смысле равен тангенсу числа t в новом смысле (так как для острых углов верна формула tg t = sin t/ cos t).
Тангенс числа t обозначается tg t.
Определения синуса и косинуса, которые вы сейчас прочитали, — это те же самые определения, что были даны в предыдущем
27
параграфе, только сформулированные более аккуратно. В предыдущем же параграфе было объяснено, почему для острых углов эти определения согласуются с прежними.
Кроме синуса, косинуса и тангенса используются также и менее употребительные функции котангенс, секанс и косеканс, которые определяются так:
ctg t = cossin tt; sec t = cos1 t; cosec t = sin1 t.
Теперь, когда мы определили тригонометрические функции числового аргумента, можно узнать, чему равны тригонометрические функции не только острых, но и прямого и тупых углов: надо перевести величину угла в радианы и взять синус, косинус или тангенс от получившегося числа.
Задача 6.9. Заполните пустые места в следующей таблице:
α |
0◦ |
90◦ |
120◦ |
135◦ |
150◦ |
180◦ |
sin α |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos α |
|
|
|
|
|
|
|
|
|
|
|
|
|
tg α |
|
— |
|
|
|
|
Замечание. В графе для tg 90◦ мы сразу поставили прочерк, так как, по определению, tg 90◦ = sin 90◦/ cos 90◦, но cos 90◦ = 0, так что tg 90◦ не определен.
Задача 6.10. Определите котангенс, секанс и косеканс острых углов с помощью прямоугольных треугольников (аналогично тому, как мы определяли синус, косинус и тангенс).
Задача 6.11. Одна из вершин правильного шестиугольника, вписанного в тригонометрическую окружность, расположена в начале отсчета. Найдите координаты остальных его вершин.
28