Задача 24.14. Изобразите на плоскости множество точек, координаты (x; y) которых удовлетворяют следующим условиям:

§ 25. Отбор чисел на тригонометрическом круге

Повторить: § 6. Определение тригонометрических функций.

§10. Простейшие тригонометрические уравнения.

Вуравнениях, встречавшихся нам до сих пор, при отборе корней получалось так, что при проверке в ответ включалась или же отбрасывалась вся серия целиком. В этом параграфе мы расскажем, что делать в более сложных случаях, когда часть серии в ответ входит, а часть — нет.

Пример 25.1. cos 3x = 0. sin 2x

147

Итак, нам нужно из множества всех x, представимых в виде π6 +

πk3 , где k — некоторое целое число, выкинуть посторонние корни —

те, что представимы в виде πn2 , где n — какое-то целое число.

Для этого нанесем на тригонометрический круг все числа вида x = π6 + πk3 , где k Z (рис. 25.1а).

При этом получится 6 точек, обозначенных на рис. 25.1а. Эти точки появляются, если взять любые 6 последовательных значений n, при остальных n точки будут повторяться. Более того, ясно, что всякое число, которому соответствует одна из отмечен-

ных на рис. 25.1а точек, имеет вид π6 + πk3 для некоторого целого k. Если нанести на этот рисунок еще и точки, соответствующие

148

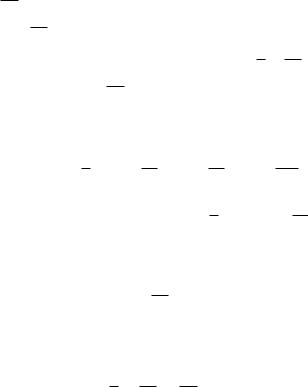
числам вида πn, то у нас получится рис. 25.1б (точки, соответ-

2 πn

ствующие числам 2 , отмечены белыми кружками). Ответом к нашему уравнению будут числа, представимые в виде π6 + πk3 и при этом не представимые в виде πn2 . Иными словами, решения урав-

нения — числа, которым соответствуют черные кружки, не совпадающие с белыми. Обращаясь к рис. 25.1б, видим, что таких кружков ровно четыре, и каждому из них соответствует бесконечная серия значений x: π6 + 2πn; 56π + 2πn; 76π + 2πn; 116π + 2πn.

Можно также объединить первую серию с третьей, а вторую — с четвертой. Тогда ответ запишется так: x = π6 + πn; x = 56π + πn

(n Z).

Мы не случайно при записи системы

x = π6 + πk3 ;

использовали две разные буквы для обозначения «произвольного целого числа»: ведь если x = π6 + πk3 = πn2 , где k 6= n, то x — все равно посторонний корень. Например, так будет при k = 4 и n = 3 (получается посторонний корень 3π/2).

Попробуем действовать так же, как и в предыдущем примере: нанесем на тригонометрический круг черные точки — числа вида π + 2πk и белые точки — числа вида 3πn. То, что получится, изображено на рис. 25.2.

149

кватно: верно, что все такие числа изображаются одной из белых точек на рис. 25.2, но неверно, что все числа, соответствующие белым точкам, имеют вид 3πn с целым n: белым точкам на рис. 25.2 соответствуют и числа π, 2π, 4π, 5π и т. д.

Вообще, изображение множества чисел на тригонометрическом круге будет адекватно, только если это множество «имеет период 2π»: вместе с каждым числом x содержит числа x − 2π и x + 2π. В частности, будет иметь период 2π множество решений уравнения, обе части которого имеют период 2π как функции от x.

Доведем теперь до конца решение уравнения cos(x/2) = 0. sin(x/3)

Все, что нам нужно, — выяснить, для каких целых чисел k число x = π+2πk окажется посторонним корнем. Это будет тогда, когда найдется такое число n Z, что π + 2πk = 3πn. Сокращая в этом равенстве на π, получаем вопрос, к которому все сводится: для каких k Z существует такое n Z, что 1 + 2k = 3n?

Чтобы ответить на этот вопрос, выразим k через n: k =

k = 3m + 1 (m Z). Итак, мы получили ответ на наш вопрос: посторонние корни получаются при k = 3m + 1, m Z. Нас же интересуют как раз все остальные k. Ясно, что сказать «k 6= 3m+

150

Указание к пункту а). При всех x верны неравенства | sin 6x| 6 1, | cos 8x| 6 1. Следовательно, sin 6x cos 8x = 1 тогда и только тогда, когда оба сомножителя одновременно равны 1 или −1.

√

Задача 25.4. а) Решите уравнение cos x + cos(x 2) = 2.

б) При каких значениях a уравнение cos x + cos(ax) = 2 имеет бесконечно много решений?

Приложение. Линейные неопределенные уравнения с двумя неизвестными

При отборе корней тригонометрических уравнений иногда приходится отвечать на вопросы наподобие: «для каких k Z существует такое n Z, что 44k + 6 = 166n»? Посмотрим на этот вопрос немного с другой стороны: выясним, для каких вообще целых k и n выполняется равенство 166n − 44k = 6. Такого рода задачи называются неопределенными уравнениями (точнее говоря, линейными неопределенными уравнениями с двумя неизвестными, но эти уточняющие слова мы будем опускать, поскольку других неопределенных уравнений нам не встретится). Расскажем, как можно решать такие уравнения.

Первое, что надо сделать для решения неопределенного уравнения, — это найти наибольший общий делитель коэффициентов при неизвестных и попробовать сократить на него обе части уравнения (разумеется, свободный член должен при этом остаться целым числом). Рассмотрим, например, уравнение 21k − 24n = 8. Наибольший общий делитель коэффициентов равен 3, и сократить на него не удается, так как 8 на 3 не делится. Тогда можно сразу сказать, что это уравнение решений в целых числах не имеет. В самом деле, если (k; n) — решение этого уравнения1, то левая

1В этом приложении под «решением» мы всегда понимаем целочисленное решение.

152

неопределенное уравнение, но его коэффициенты уже меньше, чем у исходного. Проделаем с этим новым уравнением ту же операцию, что и c исходным: выразим из него ту неизвестную, коэффициент при которой меньше по абсолютной величине (на сей раз это будет n), и выделим из получающейся дроби целую часть:

ся. В самом деле, нам надо выяснить, для каких целых v чис-

v = 2u − 3, где u — любое целое число! (дело тут, конечно, в том, что в неопределенном уравнении v = 2u − 3 коэффициент при v равен единице). Теперь, чтобы получить решения исходного уравнения, нам осталось последовательно выразить v через u, s через v, t через s, n через t и k через n. Отправимся в обратный путь:

шение получено: k = 83u−102, n = 22u−27, где u — произвольное целое число. Стало быть, ответ на наш исходный вопрос таков: пусть k — целое число. Тогда 44k + 6 = 166n для некоторого n Z тогда и только тогда, когда k = 83u − 102, где u Z.

154