в этом случае координаты ее точек задать рациональными выражениями от переменной t? Ответ на этот вопрос зависит от уравнения кривой. Если в обеих частях уравнения стоят многочлены от x и y степени не выше второй, то задать точки кривой с помощью рациональных функций от одной переменной всегда удается (примеры — в задаче 21.11). Если же кривая задана уравнением степени больше 2, то, как правило, задать координаты ее точек рациональными функциями невозможно: так обстоит дело уже для кривой x3 + y3 = 1.

Задача 21.11. Задайте с помощью рациональных функций координаты точек следующих кривых:

а) эллипса с уравнением x2 + 4y2 = 1;

б) гиперболы с уравнением xy = 1;

в) гиперболы с уравнением x2 − y2 = 1.

Указания. б) Если x = t, то y = 1/t. в) Разложите левую часть на множители.

Задача 21.12. а) Укажите пять решений уравнения x2 + y2 = 1 в положительных рациональных числах.

б) Укажите пять решений уравнения a2 + b2 = c2 в натуральных числах.

§ 22. Преобразование произведения в сумму и суммы в произведение

Напишем одну под другой формулы синуса суммы и синуса разности:

sin(α + β) = sin α cos β + cos α sin β; sin(α − β) = sin α cos β − cos α sin β.

Сложив эти формулы, получим sin(α+β)+sin(α−β) = 2 sin α cos β, или

sin α cos β = 12 (sin(α + β) + sin(α − β)).

115

Задача 22.2. Докажите тождества:

а) sin(α + β) sin(α − β) + sin(β + γ) sin(β − γ) +

+ sin(γ + α) sin(γ − α) = 0;

б) 4 sin α sin(π/3 − α) sin(π/3 + α) = sin 3α;

в) cos α + cos 2α + cos 6α + cos 7α = 4 cos α2 cos 52α cos 4α.

Задача 22.3. В предположении, что α + β + γ = π, докажите равенства:

в) sin2 α + sin2 β + sin2 γ = 2 + 2 cos α cos β cos γ.

Задача 22.4. Пусть в треугольнике против сторон a, b, c лежат соответственно углы α, β, γ. Докажите формулы:

Эти формулы называются формулами Региомонтана, или теоремой тангенсов.

Задача 22.5. а) В предположении, что α + β + γ + δ = π, докажите тождество:

sin α sin γ + sin β sin δ = sin(α + β) sin(β + γ).

б) Четырехугольник ABCD вписан в окружность. Докажите, что AB·CD+BC·AD = AC·BD (во вписанном четырехугольнике сумма произведений противоположных сторон равна произведению диагоналей — теорема Птолемея).

Формулы, которыми мы занимались в этом параграфе, применяются в радиотехнике. Пусть нам надо передать по радио голос диктора частотой, скажем, 300 . На таких низких частотах вести радиопередачу невозможно: частоты радиоволн, применяемых для радиовещания, могут измеряться миллионами . Волны

118

Рис. 22.2.

таких частот используют так. Пока диктор молчит, в эфир идут только радиоволны высокой частоты ω (несущая частота — см. график на рис. 22.2а).

Никакой информации с этим сигналом не передается. Пусть теперь диктор начал издавать звуки с частотой η (η много меньше, чем ω); тогда в эфир идет сигнал u = (A sin ηt) sin ωt. Примерный график его представлен на рис. 22.2б. Можно сказать, что амплитуда колебаний высокой частоты ω сама претерпевает колебания с низкой частотой η. Как говорят, высокочастотный сигнал модулируется низкочастотным (все сказанное — лишь грубая схема того, что на самом деле происходит в приемнике).

Преобразуем выражение для модулированного сигнала:

u = A sin ηt sin ωt = A2 cos(ω − η)t − A2 cos(ω + η)t.

Как видите, наш модулированный сигнал — не что иное, как сумма сигналов с частотами ω + η и ω − η. Так что когда говорят, что радиостанция ведет передачу на частоте, скажем, ω = 10, то надо помнить, что фактически в эфир идут не только радиоволны частоты ω, но и волны всех частот из интервала [ω −η; ω + η] где η — максимальная частота полезного сигнала, передаваемого радиостанцией. Значит, несущие частоты разных радиостанций не могут быть слишком близки друг к другу: если отрезки [ω −η; ω + η] будут перекрываться, то радиостанции будут мешать друг дружке.

Еще одно приложение формул из этого параграфа — вычисление суммы косинусов или синусов чисел, образующих арифме-

119

тическую прогрессию (в физике такие вычисления используются при исследовании явления дифракции).

Пусть нам надо упростить выражение

cos α + cos(α + h) + cos(α + 2h) + . . . + cos(α + 10h).

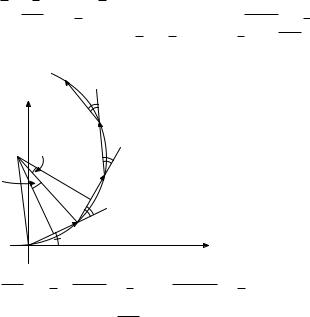
Для начала решим эту задачу геометрически, а потом покажем, как к ней можно применить наши формулы. Рассмотрим следующие векторы: a0 = (cos α; sin α), a1 = (cos(α + h); sin(α + h)), . . . , a10 = (cos(α + 10h); sin(α + 10h)). Очевидно, искомая сумма — это абсцисса вектора a0 + a1 + . . . + a10. Найдем эту сумму векторов.

Для этого отложим OA1 = a0 от начала координат, A1A2 = a1 от точки A1 и т. д. (рис. 22.3). Тогда a0 + a1 + . . . + a10 = OA11.

Рис. 22.3. OA1 = a0, A1A2 = a1,. . . , A10A11 = a10.

Чтобы найти координаты вектора OA, найдем его длину и угол наклона к оси абсцисс. Для этого заметим, что каждый из отрезков OA1, A1A2,. . . имеет длину 1 и повернут относительно предыдущего на один и тот же угол h радиан. Следовательно, точки O, A1, A2, . . . , A11 лежат на одной окружности. Ее центр Z является точкой пересечения серединных перпендикуляров к отрезкам OA1 и A1A2. Если F Z и GZ — эти перпендикуляры, то F ZG = h, так что F ZA1 = h/2 и радиус окружности R равен F A1/ sin F ZA1 = 1/2 sin(h/2) (напомним, что длины от-

120

резков OA1 и A1A2 равны единице). Так как, очевидно, OZA1 = = A1ZA2 = . . . = A10ZA11 = h, то OZA11 = 11h, и из равнобедренного треугольника OZA11 имеем

Чтобы найти угол наклона вектора OA11 к оси абсцисс, заме-

тим, что центральный угол A1ZA11 = 10h, так что вписанный

^

угол A11OA1, опирающийся на дугу A1A11, равен 10h/2 = 5h, а A11OX = A11OA1 + α = α + 5h. Стало быть,

Сопоставляя две записи для координат вектора OA11, получаем формулы:

cos α + cos(α + h) + cos(α + 2h) + . . . + cos(α + 10h) =

Первая из этих формул — это то, к чему мы стремились, вторая получилась в качестве побочного продукта.

Как видите, вычисления оказались довольно длинными. К тому же читатель-педант может заметить, что чертеж на рис. 22.3 получается только для достаточно малых h, а при больших h ломаная OA1 · · · A10A11 может обойти всю окружность, и не один раз, так что чертеж будет другой. На самом деле наша формула верна при всех α и h (если только знаменатель sin(h/2) не равен нулю; но последнее возможно только если h = 2πn для некоторого целого n, а тогда и без всякой формулы ясно, что сумма равна

121