Каждая строка обозначает канал измерения и имеет свою суммарную погрешность. Разница между каждым каналом может быть порядка 10. Сравнение суммарных погрешностей является одним из критериев качественного подбора контрольно-измерительного оборудования, должны быть примерно одинаковыми и отличаться только каналом измеряемого выходного параметра.

Приборы и устройства измерения выходного параметра могут быть классом ниже, но и погрешность будет больше, т.к. измерительные приборы будут страться измерить шум, а его невозможно измерить точно.

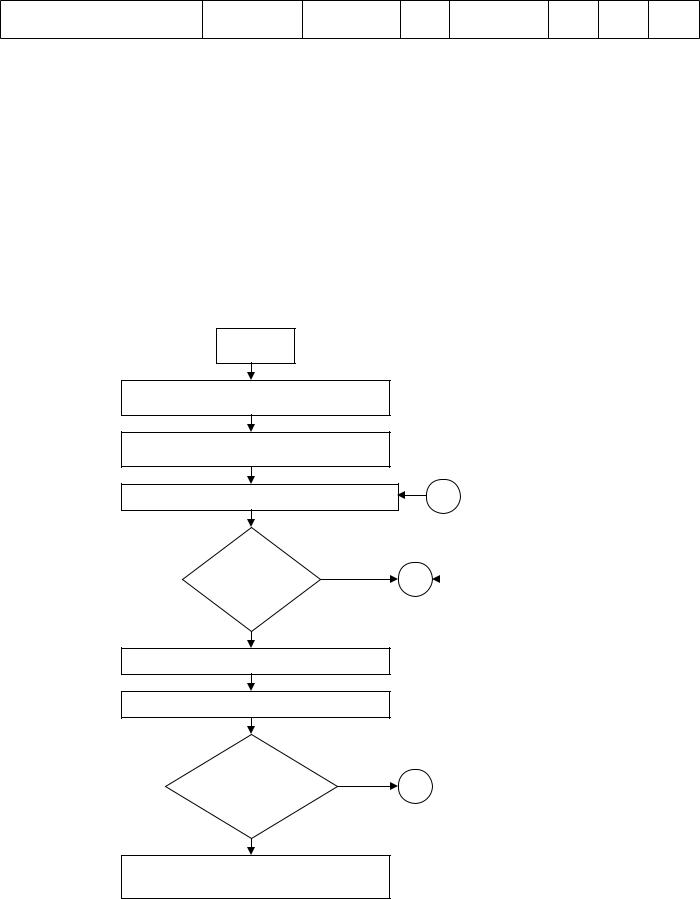
Структура блока технологического оснащения

Информационная модель - окончательно выбранный состав Xi контрольно-испытательного оборудования, датчиков, анализирующих устройств, значения их погрешности, перечень методик и руководителей для управления и эксплуатации контрольно-испытательного оборудования.

Расчёт погрешности оборудования

требованиям

нет

Информационная модель технологического оснащения

Рис.19. Структура блока технологического оснащения

30

В технологическое оснащение входят:

-контрольно-испытательное оборудование;

-приборы, датчики контроля;

-устройства имитации воздействия;

-описание технологических процессов.

Расчет погрешностей оборудования (методических и инструментальных)

Источники ошибок:

1. Приборные погрешности

-неправильные измерения датчика;

-неправильные показания индикатора (точность индикатора не соответствует точности датчика).

2. Методические погрешности

-ошибки наблюдателя (оператора). Делятся на субъективные (плохое настроение) и объективные (неправильный метод).

3. Случайные погрешности

-шумовые воздействия (воздействия неучтенных факторов).

Классы ошибок:

-систематические;

-случайные.

Систематические ошибки - такие ошибки, у которых среднее значение последовательных измерений отклоняются от известного точного значения в течение длительных измерений независимо от их числа. К ним относятся погрешности прибора, связанные с его конструкцией, погрешности, связанные с методом измерений.

Систематическая ошибка устраняется путем построения графика, который сравнивается с эталонным, и устраняется погрешность калибровки (δк). Указанная погрешность калибровки учитывается при последовательных измерениях прибора, путем прибавления или вычитания указанной погрешности.

Систематическую ошибку можно оценить с помощью калибровки прибора по известному эталону.

ср 12 ... n2

Случайные погрешности возникают при влиянии разовых случайных факторов и определяется по формуле:

Y

Yср N j , 1 Yj Yср , сл 2j

изм

Из случайной и систематической погрешности рассчитывается истинная погрешность. Истинная и случайная погрешности подчиняются нормальному закону распределения событий.

31

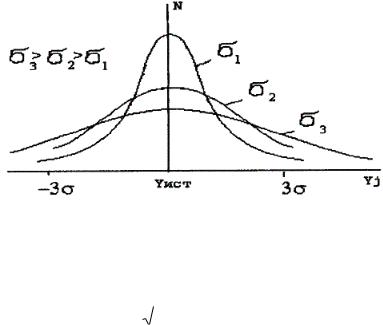
Рис.20. График систематической и случайной погрешности

где - теоретическое отклонение или дисперсия рассеяния измерений относительно

среднего Y или Yист;

S = - эмпирическое отклонение, рассеяние относительно Yср.

Для определения вида кривой проводится совокупность измерений:

-генеральная совокупность N , теоретические параметры – δ, Yист = M{Yi}

-выборка N = n, теоретические параметры – S, Yj ср.

M{Yi} – математическое ожидание измерений параметра.

При N достаточно истинное значение, когда математическое ожидание M{Y} перестает изменяться (математическое истинное значение).

M{Yj} M,{совокупносYj} ти(N )

Смещение кривой Гаусса называется эксцессом относительно математического ожидания. Для избежания эксцесс (Е) и асимметрии (А) используются следующие методы коррекции

измерений:

-метод обобщения оценок;

-метод наименьших квадратов (МНК) («Планирование эксперимента при поиске оптимальных условий», Ю.П. Адлер, стр.141);

-устойчивые методы оценивания (УМО).

В зависимости от величины ошибки могут быть приняты различные величины вероятности попадания в ±3δ или достоверности измерения.

P – вероятность попадания измерений в установленные границы измерения (±3δ). Устанавливается заказчиком или нормативными документами.

Типовые значения P:

Р=0,99 - при лабораторных измерениях; Р=0,95 - при технических измерениях;

Р=0,90 - при технических измерениях новых объектов; Р=0,82 - критическое значение вероятности, когда устанавливается адекватность

математической модели исследуемому объекту или процессу; Р=0,75 - вероятность для вновь исследуемых объектов или процессов, неизвестных явлений;

32

Р=0,6; 0,5 - при экспериментальных исследованиях с первичным описанием математической моделью, не определены достаточно точно существенные факторы, влияющие на объект или процесс.

В процессе эксперимента определяется эмпирическая дисперсия S по формуле:

где (N-1 ) - потеря статистической степени свободы для расчета Yi (ν – статистическая степень свободы).

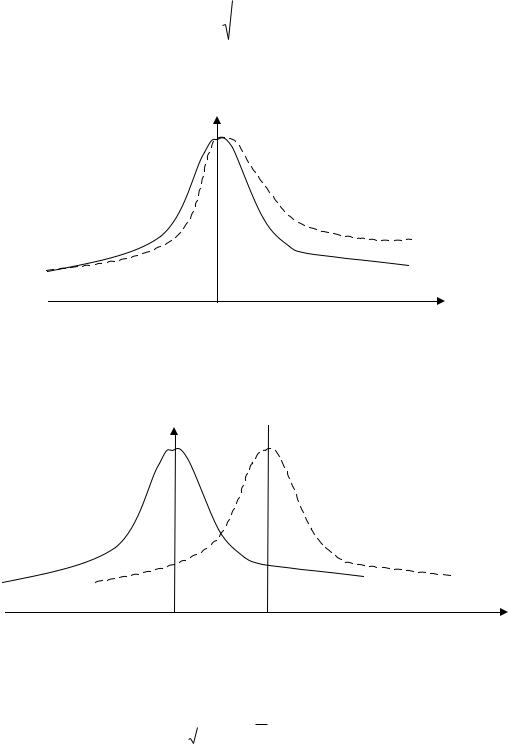
Показатель ассиметрии и эксцесса Ассиметрия – несоответствие правой и левой ветвей.

Рис.21. График ассиметрии

Эксцесс – смещение относительно оси.

Рис.22. График эксцесс.а

Если кривая Гаусса будет нормальной и соответствовать допустимым значениям вероятности (Р) и эксцесса, то расчет вероятности ведется только с помощью МНК. Этот метод наиболее простой для расчета математической модели и основан на критерии минимальной суммы квадратов отклонений Y (измерений значения выходного параметра) от среднего значения.

(yэ y)2 min

33