
- •Содержание
- •ВВЕДЕНИЕ
- •Схема взаимосвязей научных исследований и исполнителей
- •Классификация наук
- •Мировая классификация наук:
- •Российская классификация наук:
- •Российские академии
- •Виды научной деятельности
- •Классификация методик научных исследований
- •Виды научных исследований
- •Основные принципы организации научных исследований
- •Руководящие документы в организации, научной деятельности
- •Организационная структура управления образованием и наукой
- •ОБОБЩЕННЫЙ АЛГОРИТМ НАУЧНЫХ ИССЛЕДОВАНИЙ
- •БЛОК АПРИОРНЫХ ИССЛЕДОВАНИЙ
- •Априорный анализ и разработка структурной модели априорного модуля
- •Обобщенная схема исследования
- •Конструктивно-технологический анализ объекта
- •3. Тепловые нагрузки
- •4. Трение и износ
- •Схема влияния объектно-эксплуатационных факторов.
- •Результаты блока априорного анализа
- •Постановка задачи
- •БЛОК ТЕХНОЛОГИЧЕСКОГО ОСНАЩЕНИЯ (БТО)
- •Технологическое оснащение
- •Модуль отбора факторов
- •Выбор и разработка оборудования
- •Структура блока технологического оснащения
- •БЛОК ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
- •Принятие решений перед планированием эксперимента
- •Выбор интервалов варьирования.
- •1. Метод априорного ранжирования
- •2. Метод случайного баланса
- •Пример построения диаграммы
- •Основные термины планирования эксперимента
- •1. Выбор математической модели
- •Типы регрессионных моделей
- •2. Определение интервала, диапазона Xi
- •3.Выбор плана эксперимента. Типы планов экспериментальных исследований
- •Классический план эксперимента
- •Латинские планы
- •Греко-латинские планы
- •Гипер-греко-латинский план (ГГЛП)
- •Комбинационные планы
- •Планы на основе матрицы Адамара
- •1. Планы 1-го порядка.
- •1.1. План полного факторного эксперимента (ПФЭ)
- •Свойства планов ПФЭ: ПЭФ 2х2
- •Геометрическая интерпретация плана и его математической модели. ПЭФ 2
- •2. План дробного факторного эксперимента ДФЭ
- •Пример плана ДФЭ: 24-1
- •Пример плана ДФЭ: 25-2
- •Планы 2-го порядка
- •Ортогональный центральный композиционный план ОЦКП.
- •Рототабельньй центральный композиционный план РЦКП.
- •План Бокса (Вк)
- •План Бокса - Бенкена (В-В)
- •План Рехтшафнера
- •Технологические рекомендации по результатам планирования
- •БЛОК ОБРАБОТКИ ДАННЫХ
- •Алгоритм предварительной обработки данных
- •Алгоритм вторичной обработки экспериментальных данных
- •БЛОК ИНТЕРПРЕТАЦИИ И АНАЛИЗА
- •Определение параметров интерпретации
- •Интерпретация регрессионной модели
- •Анализ регрессионных зависимостей

БЛОК ОБРАБОТКИ ДАННЫХ
Блок обработки данных состоит из двух этапов:
-предварительная обработка данных (первичная);
-окончательная обработка данных (вторичная). Цель предварительной обработки данных:
-получить параметры выборки экспериментальных данных из n опытов, получениить эмпирическое среднеквадратическое рассеивание (S) и оценку математического ожидания (Ycp).
-определить выбросы экспериментальных данных, т.е. выявить замеры, которые резко отличаются от общей совокупности, провести их замену или смоделировать;
-определить нормированность распределения экспериментальных данных.
Алгоритм предварительной обработки данных
1. Постановка задачи. Исходные данные.
|
|
|
X11 |
X12 |
... |
X1K |
|
|
|
|
|
||||
X |
|
|
X 21 |
X 22 |
... |
X 2 K |
- матрица (n x k.) - план эксперимента. |
|
|||||||
|
|
|
| |
| |
| |
| |
|
|
|
|
X N 1 |
X N 2 |
... |
X NK |
|
X – большие, т.к. замеры получаем в конкретных физических единицах (не безразмерные).
|
|
|
|
Y1 |
|
|
|
|
|
Y11 |
Y12 |
... |
Y1M |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Y |
|
|
Y2 |
, N 1 |
|
Yj |
|
|
Y21 |
Y22 |
... |
Y2 M |
- матрица (NxM). |
|
|
|
|
|||||||||||
|
|
|||||||||||||
|
|
|
|
| |
|
|
|
|
|
| |
| |
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
YN |
|
|
|
|
|
YN1 |
YN 2 |
... |
YNM |
|
Вкаждом эксперименте последовательность опытов (в столбцах) отличается друг от друга и носит рандомизированный характер (случайный). Это делается для снижения монотонного накопления шумовых воздействий.
За счет рандомизации – рассеяние однородное.
ВY – матрице строка является распределением экспериментальных данных, которое может носить и теоретический и экспериментальный характер (эмпирическое распределение дисперсии).
Необходимо определить наличие выбросов аномальных измерений Y, нарушение условий проведения опытов и нормальных распределений данных в каждой строке (Y*м).
2. Этапы предварительной обработки данных.
1). Расчет эмпирических средних по строкам:
Y mj Yjm - построчное среднее m j
Yjm
Y mj N M - среднее по эксперименту
N M
2) Дисперсия воспроизводимости, построчная дисперсия:
|
|
(Y |
|
|
|
)2 |
|
|
|
|
Y |
|
|
||||
SBj2 |
|
|
mj |
|
j |
|
, m 1 |
|
|
|
|
||||||
|
|
|
|
|
||||
SBN2 |
|
SBj2 |
|
|
|
|
|
|
M |
|
|
|
|
|
|||
m j |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
При подсчете среднего значения первая степень свободы считается уже использованной,
68

поэтому в знаменателе (m-1).
Эта дисперсия показывает характеристики рассеивания экспериментальных данных в каждом опыте. Чем она меньше, тем меньше влияние побочных эффектов и выше точность оценки выходного параметра. Некоторые физические эксперименты являются не воспроизводимыми, т.е. их повтор невозможен (например, летные испытания на природе).
3) Определение статистической однородности дисперсии воспроизводимости: Статистический нуль → гипотезы → H0
Критерий Фишера:
S 2
SB2(i 1) кр ; i ; i 1
Вкаждой использованной строке считается эмпирическая дисперсия и определяется их соотношение.
H0: Если расчетное значений меньше табличного (определенного по α,νi,νi+1), то считаются дисперсии однородными на заданном уровне вероятности α (α=1-p, где p - вероятность).
Втом случае, если устанавливается неоднородность, то это означает, что в одном из распределений присутствует выброс или при проведении экспериментов не учтен существенный
фактор (либо просто грубая ошибка).
4) Оценка отклонений от среднего: BiF F
H0: V SBi 100% 33%
Yi
Если условие нарушается, то это означает присутствие выброса или неустановленного существенного фактора (например, изменение температуры и давления на улице → в лаборатории).
5) Оценка отклонений среднего по Т-критерию:
y j |
SBj |
|
t 2 |
yiэ y j |
SBj |
|
t 2 : H0 |
||
|
|
|
|
|
|
||||
|
j |
j |
|||||||
|
|
|
|
|
|
|
|||
t - критерий Стьюдента, используемый для оценки распределения экспериментальных данных при малом количестве измерений.
t определяется по таблице по величине α (достоверности) и количеству экспериментальных данных.
H0: Если экспериментальные данные в первой выборке удовлетворяют значению неравенства, то они считаются однородными и не имеют выбросов.
6) Оценка однородности дисперсии воспроизводимости по x2-критерию:
|
S 2 |
|
|
S |
2 |
|
||||
H0: |
|
i Bi |
i2 |
|
|
|
i Bi |
условие |
||
|
2 |
|
|
2 |
||||||
|
|
x |
2 |
|
|
|
|
xp |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Дисперсия σi считается по каждому из опытов однородной, если удовлетворяет неравенству, т.е. находится в диапазоне установленным x2-критерием. В противном случае, σi, неудовлетворяет неравенству, считается неоднородной, и в этом опыте необходимо выявить выброс или дополнительное воздействие неучтенных факторов.
7) Проверка нормальности распределения экспериментальных данных по условиям каждого
опыта:
A Aconst , E Econst
Ac 3
 D( Ai ) Ec 5
D( Ai ) Ec 5
 D(E)i
D(E)i
69

|
|
q |
|
p |
|
|
|
|
|
|
|
|
p/2 |
|
|
p/2 |
«хвост» |
|
|
|
|
||
|
|
|
|
|
|
-α/2 |
|
|
|
|
+α/2 |
0 |
-3σ |
|
Y{•} |
+3σ |
yj |
|
M{Yj} |
||||
|
|
|
|
|
|
Грубо |
центр |
|
|
|
|
говоря Yj |
|
|
|
|
|
Рис.50. Проверка нормальности
q –число данных в первой выборке
M{Yj} – математическое ожидание истинного значения выходного параметра p – вероятность попадания параметра в интервал
3σ – утроенное значение дисперсии выходного параметра
Значение p может варьироваться в интервале от 0,90 до 0,99. «Хвосты» могут быть тяжелыми и нормальными.
Н0: Ас – ассиметрия. Н0: Ес - эксцентриситет
Ассиметрия рассчитывается по табличным данным (дисперсионная симметрия).
Если первичная обработка данных не устанавливает выбросов и отклонений от нормальности распределения, считается возможным применять на этапе вторичной обработки метод наименьших квадратов для расчета значений коэффициентов регрессионного уравнения.
Если нормированность не устанавливается, то применяется для расчетов bi: обобщенный метод наименьших квадратов; устойчивые методы обработки.
Алгоритм вторичной обработки экспериментальных данных
Входными условиями для этапа вторичной обработки экспериментальных данных по МНК являются: |x|, |y|, N(•) по каждому опыту матрицы Y.
1) Определение коэффициентов регрессионного уравнения:
70

b1 |
|
( 1) y1 ( 1) y2 ( 1) y3 ( 1) y4 |
|
||||
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
b2 |
|
|
( 1) y1 |
( 1) y2 |
( 1) y3 |
( 1) y4 |
|
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
b0 |
|
|
( 1) y1 |
( 1) y2 |
( 1) y3 |
( 1) y4 |
|
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
Пример:
|
|
|
|
|
|
|
|
Таблица 27 |
|
|
|
|
|
|
X1 |
X2 |
X1X2 |
|
Yср |
1 |
|
|
|
|
- |
- |
+ |
2 |
|
2 |
|
|
|
|
+ |
- |
- |
4 |
|
3 |
|
|
|
|
- |
+ |
- |
6 |
|
4 |
|
|
|
|
+ |
+ |
+ |
8 |
|
|
|
|
|
|
b1 |
b2 |
b12 |
|
|
b ( 1) 2 ( 1) 4 ( 1) 6 ( 1) 8 1 |
|||||||||
1 |
|
|
8 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
b2 |
|
2 |
|
|
|
|
|||
|
|
|
4 |
|
|
|
|
|
|
b12 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
b |
20 |
5 |
|
|
|
|
|||
0 |
|
|
4 |
|
|
|
|
|
|
b0 = 5, так как x0 → все «+» |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Математическая модель: |
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
2) Определение остаточной дисперсии (S2остаточн.), или дисперсии адекватности(S2ад.):
Sост2 [n q (yjM yjЭ )2] ост1 ,где ост ( qj ) l
либо
71

|
N |
|
|
Sад2 |
yi2 ] |
, где N (k 1) |
|
i 1 |
|||
|
|||
|
|
q, N – количество замеров в первом опыте
l, k – количество коэффициентов регрессионного уравнения Пример Провели полный факторный эксперимент 23.
Число степеней свободы будет
N (k 1) 8 (3 1) 4
3)Определение дисперсии коэффициентов регрессионного уравнения
S02{b0 } c0 Sост2
Si2{bi } ci Sост2
Sij2{bij } cij Sост2
4)Проверка значимости коэффициентов
Можно осуществлять двумя способами: проверкой по t-критерию Стьюдента или построением доверительного интервала. При использовании полного факторного эксперимента доверительные интервалы (в том числе и эффектов взаимодействия) равны друг другу.
Прежде всего надо найти дисперсию коэффициента регрессии S{2b j } . Она определяется по формуле
S 2
S{2bj } N{y} , если параллельные опыты отсутствуют.
Из формулы видно, что дисперсии всех коэффициентов равны друг другу, так как они зависят от ошибки опыта и числа опытов.
Теперь построим доверительный интервал ( Δbj )
bj tS{bj }
Здесь t – табличное значение критерия Стьюдента при числе степеней свободы, с которыми определялась S{2y} , и выбранном уровне значимости (обычно 0,05); S{b j } - квадратичная ошибка коэффициента регрессии
S{b j } 
 S{2b j }
S{2b j }
Формулу для доверительного интервала можно записать в следующей эквивалентной форме:
b tS{bj }
j 
 N
N
Коэффициент значим, если его абсолютная величина больше доверительного интервала. Доверительный интервал задается верхней и нижней границами bj bj и b j bj .
Для отыскания значения t–критерия можно воспользоваться таблицей, фрагмент из которой преведен в табл. 60.4.
Таблица построена следующим образом. Столбцы соответствуют различным степеням свободы и значениям критерия.
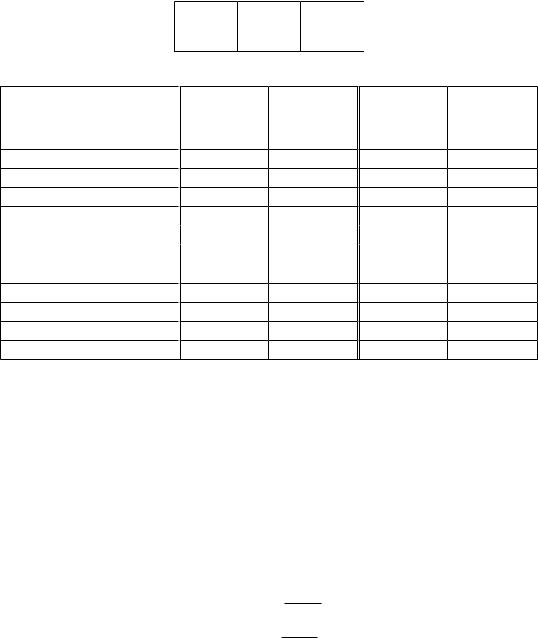
Пусть в двух различных случайно оказались два численно равных коэффициента регрессии. Доверительные интервалы для них оказались различными. Из них значим только второй
|
|
Таблица 28 |
Задача |
b j |
b j |
72
|
|
1 |
5,3 |
±5,5 |
|
|
|
|
|
2 |
5,3 |
±2,6 |
|
|
|
|
|
|
|
|
|
Таблица 29 |
|
Число |
Значения |
Число |
Значения |
Число |
Значения |
||
степеней |
степеней |
степеней |
|||||
t–критерия |
t–критерия |
t–критерия |
|||||
свободы |
|
свободы |
|
|
свободы |
|
|
1 |
12,71 |
11 |
|
2,201 |
21 |
2,080 |
|
2 |
4,303 |
12 |
|
2,179 |
22 |
2,074 |
|
3 |
3,182 |
13 |
|
2,160 |
23 |
2,069 |
|
4 |
2,776 |
14 |
|
2,145 |
24 |
2,064 |
|
5 |
2,571 |
15 |
|
2,131 |
25 |
2,060 |
|
6 |
2,447 |
16 |
|
2,120 |
26 |
2,056 |
|
7 |
2,365 |
17 |
|
2,110 |
27 |
2,052 |
|
8 |
2,306 |
18 |
|
2,101 |
28 |
2,048 |
|
9 |
2,262 |
19 |
|
2,093 |
29 |
2,045 |
|
10 |
2,228 |
20 |
|
2,086 |
30 |
2,042 |
|
|
|
|
|
|
∞ |
1,960 |
|
В действительности чем уже доверительный интервал (при заданном α), тем с большей уверенностью можно говорить о значимости коэффициента.
Рабочее правило: если абсолютная величина коэффициента больше, чем доверительный интервал, то коэффициент значим. Если больше нравится проверять значимость коэффициента по t–критерию, то воспользуйтесь формулой
t |
|
bj |
|
S{b j } |
|||
Вычисленное значение t–критерия сравнивается с табличным при при заданном α и соответствующем числе степеней свободы. Полученные выводы о значимости коэффициентов должны совпадать с предыдущими.
Так производится проверка значимости коэффициентов. Н0:
b0крит t
 S02{b0 } biкрит t
S02{b0 } biкрит t
 Si2{bi } biкрит bi min
Si2{bi } biкрит bi min
Н0 (гипотеза): Если значение коэффициента регрессионного уравнения удовлетворяет неравенству, то коэффициент регрессии считается статически незначимым на заданном уравнении вероятности и может быть изъят из уравнения регрессии.
Для математической модели, полученной по ортогональным планам, при выбросе незначимых коэффициентов остальные не пересчитываются.
5) Оценка адекватности регрессионной модели:
|
|
|
S 2 |
|
|
|
|
|
H |
0 |
: F |
ад |
F {, |
воспр |
, |
ад |
} |
|
||||||||
|
|
|
кр |
|
|
|||
|
|
|
S{2y} |
|
|
|
|
|
Yср. по плану – среднее значение выходного параметра по строкам и столбцам (т.е. со всеми повторами).
Если гипотеза удовлетворяется, то считается, что регрессионное уравнение адекватно, т.е.
73
