testy_tets_oktyabr2015 (1)
.docx$$согласованный режим работы
$несогласованный режим работы
$режим холостого хода
$режим короткого замыкания
$$$243В
расчетном плане при выполнении условия
![]() последовательная
и параллельная схемы замещения источника
являются
последовательная
и параллельная схемы замещения источника
являются
$$эквивалентными
$неэквивалентными
$параллельными
$последовательными
$$$244Сопротивления соединены последовательно
$$если они обтекаются одним и тем же током
$если они равны
$если они не равны
$если они обтекаются разнами токами
$$$245Во всех cлучаях преобразования замена одних схем другими, им эквивалентными,
$$ не должна привести к изменению токов или напряжений участках цепи, не подвергшихся преобразованию
$ должна привести к изменению токов или напряжений участках цепи, не подвергшихся преобразованию
$ не должна привести к изменению токов или напряжений участках цепи, подвергшихся преобразованию
$ должна привести к изменению токов или напряжений на участках цепи
$$$246Эквивалентное сопротивление цепи, состоящей из последовательно соединенных сопротивлений, равно
$$ сумме этих сопротивлений
$ произведению этих сопротивлений
$ разности этих сопротивлений
$ произведению всех сопротивлений
$$$247При последовательном соединении n сопротивлений напряжения на них распределяются U1: U2: …: Un= R1: R2: …: Rn.
$$ прямо пропорционально этим сопротивлениям
$ обратно пропорционально этим сопротивлениям
$ непропорционально этим сопротивлениям
$ по нагрузке
$$$248В частном случае
U1 / U2 = R1 / R2; U1= U R1 / (R1+ R2); U2=U R2 / ( R1+ R2),
где U — общее напряжение, действующее на участке цепи, содержащем два сопротивления R1 и R2.
$$ двух последовательно соединённых сопротивлений
$ двух параллельно соединённых сопротивлений
$ согласованно соединённых сопротивлений
$ несогласованно соединённых сопротивлений
$$$249Сопротивления соединены параллельно
$$ если все они присоединены к одной паре узлов
$ если все они присоединены к разным парам узлов
$ если все они присоединены
$ если все они не присоединены
$$$250Эквивалентное сопротивление цепи определяется из формулы
![]() ,
или
,
или
![]() .
.
$$ состоящей из n параллельно соединенных сопротивлений
$ состоящей из n последовательно соединенных сопротивлений
$ состоящей из двух параллельно соединенных сопротивлений
$ состоящей из двух последовательно соединенных сопротивлений
$$$251В частном случае эквивалентное сопротивление
 .
.
$$ параллельного соединения двух сопротивлений R1 и R2
$последовательного соединения двух сопротивлений R1 и R2
$ согласованного соединения двух сопротивлений R1 и R2
$ несогласованного соединения двух сопротивлений R1 и R2
$$$252При
параллельном соединении n
сопротивлений на рисуноке а) токи в
них распределяются
I1
:
I2
: … : In
=
![]() :
:![]() :
… :
:
… :
![]() =
G1:
G2
: … : Gn.
=
G1:
G2
: … : Gn.

$$ обратно пропорционально их сопротивлениям или прямо пропорционально их проводимостям
$ прямо пропорционально их сопротивлениям или обратно пропорционально их проводимостям
$ обратно пропорционально их сопротивлениям или обратно пропорционально их проводимостям
$ прямо пропорционально их сопротивлениям или прямо пропорционально их проводимостям
$$$253Вчастномслучае
I2
=
I1![]() ,
I3
= I1
,
I3
= I1![]() или
I2
= I1
или
I2
= I1![]() ,
I3
=
I1
,
I3
=
I1![]() .
.

$$ двух параллельных ветвей
$ двух последовательных ветвей
$ трех параллельных ветвей
$ трех последовательных ветвей
$$$254Сочетание последовательного и параллельного соединений сопротивлений
$$ смешенное соединение
$ последовательное соединение
$ параллельное соединение
$ согласованное соединение
$$$255На рисуноке б) эквивалентное сопротивление
Rэк
= R1
+
![]() =
=
![]() .
.

$$ R1 , R2 и R3 соединены смешанно
$ R1 , R2 и R3 соединены параллельно
$ R1 , R2 и R3 соединены последовательно
$ R1 , R2 и R3 параллельны
$$$256Формулы преобразования называются
R1=
 ,
R2
=
,
R2
=
![]() ,
,
![]() R3
=
R3
=
![]() ,
,
G12
=![]() ,
G23=
,
G23=
![]() ,
G31
=
,
G31
=
![]()
R12=R1+R2+![]() ,
R23=
R2+R3+
,
R23=
R2+R3+![]() ,
R31=R3+R1+
,
R31=R3+R1+![]() .
.
$$ преобразование треугольника сопротивлений в эквивалентную звезду сопротивлений
$ преобразование сопротивлений
$ преобразование треугольника сопротивлений
$ преобразование звезды сопротивлений
$$$257. Закон Ома для участка цепи
$I = U*R
$$I = U/R
$U = I/R
$U = I*R
$$$257Закон Ома применяется
$$для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений)
$для ветви
$для одноконтурной замкнутой цепи (не имеющей разветвлений)
$для одноконтурной замкнутой цепи
$$$258При написании закона Ома следует, прежде всего, выбрать .........некоторое положительное направление тока.
$$произвольно
$непроизвольно
$ на север
$ на юг
$$$259
Написание закона Ома .....Ι
=
![]() =
=
![]()
$$Для ветвивка, состоящей только из резисторов и не содержащей э. д. с., при положительном направлении тока от точки в к точке а
$Для ветви асb цепи, содержащей э. д. с. и резисторы
$Для ветви сак цепи, содержащей э. д. с. и резисторы
$Для ветви свк цепи, содержащей э. д. с. и резисторы
|
|
|
|
|
|
$$$260 Написание закона Ома ......, при положительном направлении тока от точки в к точке а
I1=
 =
=
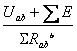
$$Для ветви асb цепи, содержащей э. д. с. и резисторы
$Для ветвивка, состоящей только из резисторов и не содержащей э. д. с
$Для ветви сак цепи, содержащей э. д. с. и резисторы
$Для ветви свк цепи, содержащей э. д. с. и резисторы

$$$261Формулу
I1=
 =
=
 называют........
называют........
$$обобщенным законом Ома
$законом Ома
$1 законом Кирхгофа
$ 2законом Кирхгофа
$$$262 Формула
I
=
![]()
$$для замкнутой одноконтурной цепи
$для многозвенных цепей
$ для индуктивных цепей
$ для емкостных цепей
$$$263..............является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
$$баланс мощностей
$ баланс токов
$баланс мостов
$ баланс сопротивлений
$$$264Величина, обратная периоду, есть
$$частота
$ время
$ напряжение
$ ток
$$$ 265Частотаесть величина, обратная .....
$$периоду
$току
$ напряжению
$ мощности
$$$ 266Частота, измеряеся в......
$$Гц
$ с
$ м
$ В
$$$
267 Формула![]() выражает
зависимость
выражает
зависимость
$$частоты от периода
$ тока от напряжения
$ напряжения от тока
$ тока от мощности
$$$ 268Диапазон частот, применяемых в технике: от сверхнизких частот– в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (– миллиметровые волны: ().
$$0.01¸10 Гц-3000 ¸ 300000 МГц
$0.01¸10 м-3000 ¸ 300000км
$0.01¸10мс -3000 ¸ 300000ч
$0.01¸10 мВ-3000 ¸ 300000В
$$$ 269Миллиметровые волны применяют (3000 ¸ 300000 МГц)
$$радиолокация, радиоастрономия
$ в системах автоматического регулирования
$ в аналоговой вычислительной технике
$ ваналоговой технике
$$$
2695.Если синусоидальное напряжение
![]() приложено
к сопротивлению r,
то через сопротивление пройдет
синусоидальный ток
приложено
к сопротивлению r,
то через сопротивление пройдет
синусоидальный ток
![]() .
.

$$Синусоидальный ток в сопротивлении
$Синусоидальный ток в емкости
$Синусоидальный ток в индуктивности
$Синусоидальный ток в сопротивлении
$$$ 270Напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу или, как говорят, совпадают по фазе. (рисунок 5.3 ,б).
$$Синусоидальный ток в сопротивлении
$Синусоидальный ток в емкости
$Синусоидальный ток в индуктивности
$Несинусоидальный ток в индуктивности

$$$ 271В данном случае сдвиг по фазе равен нулю
$$Синусоидальный
ток в сопротивлении![]()
$Синусоидальный ток в емкости
$Синусоидальный ток в индуктивности
$Несинусоидальный ток в индуктивности
$$$
272Мгновенные значения напряжения на
сопротивлении и тока в нем, связаны
законом Ома ![]()
![]()
$$При прохождении синусоидального тока через сопротивление
$При прохождении несинусоидального тока через индуктивность
$При прохождении синусоидального тока через индуктивность
$При прохождении синусоидального тока через емкость
$$$ 273Амплитуды и соответственно действующие значения напряжения и токасвязаны законом Ома
![]()
![]()
$$При прохождении синусоидального тока через сопротивление
$При прохождении несинусоидального тока через индуктивность
$При прохождении синусоидального тока через индуктивность
$При прохождении синусоидального тока через емкость
$$$ 274Чему равна промышленная частота ?
$$f = 50Гц
$f = 150Гц
$f = 250Гц
$f = 500Гц
$$$ 275 Значения Im ,Um, Em называют
$$амплитудами
$ мгновенными значениями
$ точными значениями
$действующими значениями
$$$ 276Наибольшее мгновенное значение переменной величины за период называется амплитудой,ее обозначают.....
$$Im,Um, Em
$ I,U, E
$ ,
,

$i,u, e
$$$
277 Значение Im/ называют
называют
$$действующего тока
$действующего напряжения
$мгновенного тока
$амплитуды тока
$$$ 278 Выражение для определения

$$действующего тока
$действующего напряжения
$мгновенного тока
$амплитуды тока
$$$ 279действующие значения синусоидальных токов, ЭДС и напряжения
$$меньше
своих амплитудных значений в
![]() раз.
раз.
$больше
своих амплитудных значений в
![]() раз.
раз.
$меньше
своих мгновенных значений в
![]() раз.
раз.
$больше
своих мгновенных значений в
![]() раз.
раз.
$$$
![]()
$$периодического тока
$непериодическоготока
$ переменноготока
$постоянноготока
$$$ 281Промышленная частота
$$f = 50Гц
$f = 150Гц
$f = 250Гц
$f = 500Гц
$$$
282![]() определяет
определяет
$$частоту
$ напряжение
$ круговую частоту
$ период
$$$ 283
Im/
$$действующее значение тока
$действующего напряжения
$мгновенного тока
$амплитуды тока
$$$ 284При совместном рассмотрении двух синусоидальных величин одной частоты разность их начальных фаз, называют .....
![]()
$$углом сдвига фаз.
$ частотой
$ фазами
$ круговой частотой
$$$
285.
Так
как фазовый угол синусоиды за время
одного периода Т
изменяется на
![]() рад.,
то выражение
рад.,
то выражение
![]() определяет.....
определяет.....
$$угловую частоту
$скорость
$ время
$ период
$$$
286Величину
![]() ,
характеризующую скорость изменения
фазового угла, называют
,
характеризующую скорость изменения
фазового угла, называют
$$угловой частотой
$начальной фазой
$ частотой
$ периодом
$$$ 287Значение фазы в начальный момент времени (t=0):
$$![]() и
и![]()
$ω1 и ω2
$t1 и t2
$е1 и е2
$$$
288Значения аргументов синусоидальных
функций
![]() и
и
![]() называются
называются
$$фазами синусоид,
$начальными фазами
$фазы в начальный момент времени
$сдвигом фаз
$$$
289![]()
![]() . соответствуют
. соответствуют
$$уравнения двух синусоидальных ЭДС е1 и е2
$уравнения двух несинусоидальных ЭДС е1 и е2
$уравнения двух синусоидальных токов
$уравнения двух несинусоидальных токов
$$$ 290Приведенным на рисунке соответствуют уравнения
$$графикам двух синусоидальных ЭДС е1 и е2
$графикам двух несинусоидальных ЭДС е1 и е2
$графикам двух несинусоидальных токов
$графикам двух синусоидальных токов

$$$ 291Синусоидальные токи и напряжения можно изобразить
$$графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
$графически
$записать при помощи уравнений с тригонометрическими функциями,
$представить в виде векторов на декартовой плоскости или комплексными числами.
$$$ 292Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют

$$действующим значениемпериодического тока
$значениемпериодического тока
$действующим значениемнепериодического тока
$действующим значениемпериодического напряжения
$$$
293Выражение для .........тока
![]()
$$периодического
$непериодического
$ переменного
$постоянного
$$$ 294 Наименьший промежуток времени, через которые значения токов повторяются называют
$$периодом Т
$ временем
$ участком
$отрезком
$$$ 295Токи, через равные промежутки времени в одной и той же последовательности, называются ........
$$периодическими
$непериодическими
$ синусоидальные
$ несинусоидальные
$$$ 296Только при использовании ................. тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.
$$синусоидального
$ постоянного
$ несинусоидального
$ тока х.х.
$$$ 297В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на..........
$$переменном токе
$постоянном токе
$токе х.х.
$ токе к.з.
$$$ 298Какой ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов?
$$ переменный
$ постоянный
$ток х.х
$ток к.з.
$$$ 299Для любой замкнутой электрической цепи сумма мощностей РИ, развиваемых источниками электрической энергии, равна сумме мощностей Рп, расходуемых в приемниках энергии
$$баланс мощностей
$баланс мостов
$закон Ома
$ 1закон Кирхгофа
$$$ 300Суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
$$баланс мощностей
$баланс мостов
$закон Ома
$ 1закон Кирхгофа
$$$
301Это
уравнение
![]() =
=![]() ,
или
,
или![]() .
.
представляет собой математическую форму записи
$$баланса мощностей
$баланса мостов
$закона Ома
$ 1закона Кирхгофа
$$$302
Для нахождения тока Jэк
надо зажимы a
и b
закоротить и любым способом рассчитать
ток которого замыкания Ik
, протекающий по закороченному участку
(рис. ж). При этом Jэк
=
Ik.Сопротивление
Rэк-из
схемы в режиме короткого замыкания
(рис.з) по формулеRэк=Еэк/Ik=Еэк/Jэк=1/Gэк. Ток
в ветви R (рис. и)I=Jэк![]() .
.

$$Метод эквивалентного источника тока.
$Метод эквивалентного источника э.д.с.
$ Метод наложения.
$ Метод треугольника
$$$ 303 Для нахождения тока I в произвольной ветви ab, сопротивление которой R (рисунок а), надо эту ветвь разомкнуть (рисунок б), а часть цепи, подключенную к этой ветви, заменить эквивалентным источником с э.д.с. Еэк и внутренним сопротивлением Rэк (рисунок в).

I
= =
=![]()
$$Метод эквивалентного источника э.д.с.
$ Метод эквивалентного источника тока
$ Метод наложения.
$ Метод треугольника
$$$304При
![]() Э.Д.С.
определяется по формуле
Э.Д.С.
определяется по формуле![]()
$$Ток проходит через индуктивность L
$Ток проходит через сопротивление
$Ток проходит через емкость
$Ток проходит по контуру
$$$305На рисунке показаны графики
$$синусоидальный ток, напряжение в индуктивности
$несинусоидальный ток, напряжение в индуктивности
$синусоидальный ток, напряжение в емкости
$синусоидальный ток, напряжение в резисторе

$$$306 Выражение определяет
![]()
$$напряжение на индуктивности
$ток на индуктивности
$ напряжение на резисторе
$ напряжение на емкости
$$$307Напряжение на индуктивности
$$опережает
ток на угол
![]()
$отстает
от тока на угол
![]()
$опережает ток на угол π
$отстает от тока на уголπ

$$$308Фазовый
сдвиг между…… равен
![]()
$$ синусоидальным током и напряжением в индуктивности
$несинусоидальным током и напряжением в индуктивности
$синусоидальным током и напряжением в емкости
$синусоидальным током и напряжением в резисторе

$$$309Амплитуда так же, как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома
![]()
$$синусоидальный ток, напряжение в индуктивности
$несинусоидальный ток, напряжение в индуктивности
$синусоидальный ток, напряжение в емкости
$синусоидальный ток, напряжение в резисторе
$$$310Величина
![]() ,
называется.......
,
называется.......
$$индуктивным сопротивлением
$ резистором
$ емкостным сопротивлением
$ индуктивностью
$$$311Величина
обратная индуктивному сопротивлению
![]() называется
называется
$$индуктивной проводимостью
$индуктивным сопротивлением
$ проводимостью
$ емкостный проводимостью
$$$312
Выражение
![]() показывает
соотношения между
показывает
соотношения между
$$синусоидальный ток, напряжение в индуктивности
$несинусоидальный ток, напряжение в индуктивности
$синусоидальный ток, напряжение в емкости
$синусоидальный ток, напряжение в резисторе
$$$313На рисунке показаны графики
$$синусоидальный ток, напряжение в емкости
$несинусоидальный ток, напряжение в индуктивности
$синусоидальный ток, напряжение в индуктивности
$синусоидальный ток, напряжение в резисторе

$$$314Выражение определяет
![]()
$$напряжение на емкости
$ток на индуктивности
$ напряжение на резисторе
$напряжение на индуктивности

$$$315Выражение определяет
![]()
$$ток в емкости
$напряжение в емкости
$ ток в емкости
$ ток на резисторе
$$$316Выражение
![]() показывает,
что ...
показывает,
что ...