Примеры формальных аксиоматических теорий

I. Формальное исчисление высказываний. Алфавит этой теории – это алфавит исчисления высказываний. Он состоит из трёх групп символов: пропозициональных переменных: a, b, c, d, … , б₃₄₅ , v₉₆₄ , … , логических связок: , ,  ,  ,  и служебных символов: ( , ).

Правила построения формул исчисления высказываний известны:

(Ф1): любая пропозициональная переменная является формулой.

(Ф2): если A и В – формулы, то (A  B), (A  B), (A  B), (A  B), – тоже формулы.

(Ф3): других формул нет.

Аксиомы формального исчисления высказываний делятся на четыре группы схем аксиом, включающие 11 схем. Это значит, что в нижеследующих псевдоформулах буквы A , B , C – не символы алфавита теории, вместо них можно подставлять любые формулы исчисления высказываний. Таким образом, эти 11 схем аксиом на самом деле представляют бесконечное количество аксиом.

Группа аксиом импликации:

(И1): (A  (B  A))

(И2): ((A  (B  C))  ((A  B)  (A  C)))

Группа аксиом конъюнкции:

(К1): ((A  B)  A)

(К2): ((A  B)  B)

(К3): ((A  B)  ((A  C)  (A  (B  C))))

Группа аксиом дизъюнкции:

(Д1): (A  (A  B))

(Д2): (B  (A  B))

(Д3): ((A  C)  ((B  C)  (A  B  C)))

Группа аксиом отрицания:

(О1): (A  )

(О2): (  A)

(О3): ((A  B)  (  ))

В дальнейшем будем опускать в формулах некоторые скобки, предполагая, что их можно расставить по правилам восстановления скобок § 3 главы I.

В приведённом списке аксиом отсутствует логическая связка  . Это сделано из соображений экономии: известно, что эта связка является производной – она выражается через остальные. Желающие работать с ней, должны ввести ещё следующие две схемы аксиом:

Группа аксиом эквивалентности:

(Э1): ((A  B)  ((A  B)  (B  A)))

(Э2): (((A  B)  (B  A))  (A  B))

Единственным правилом вывода в формальном исчислении высказываний является уже знакомое правило Modus ponens (MP): .

Доказательством формулы В в формальной теории исчисления высказываний называется конечная последовательность формул В₁ , … , В_n , где В_n совпадает с В, а каждая формула B_i (1  i  n) либо является аксиомой, либо получена из предыдущих формул В_j и В_k (1  < i)по правилу Modus ponens, т.е. В_k = (B_j  B_i) и применение правила (MP) таково: . Это значит, что из доказуемости формулB_j и B_j  B_i постулируется возможность сделать вывод о доказуемости формулы B_i . Это далеко не очевидный логический ход, хотя многих птешит иллюзия, что он согласуется со здравым смыслом.

Формула В, для которой существует доказательство, называется доказуемой в формальном исчислении высказываний. В этом случае будем писать В . В частности, всякая аксиома А доказуема, т.к. её доказательством является последовательность формул, состоящая из единственной формулы А.

Примеры доказательств в формальном исчислении высказываний

1. А  A

2. A  B  B  A

3.

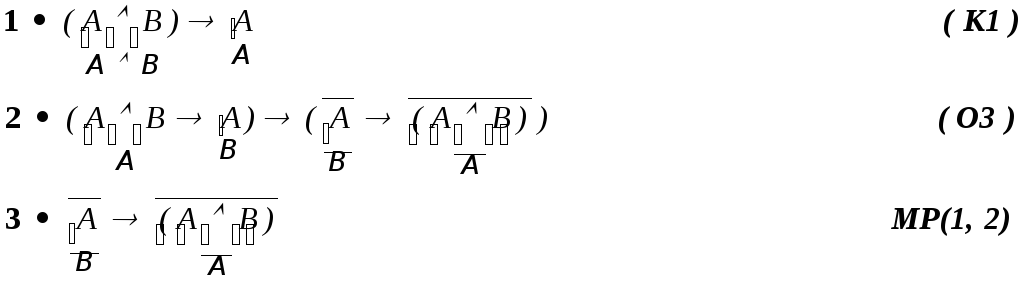
II. Формальное исчисление предикатов. Алфавит этой теории – это алфавит исчисления предикатов. Он состоит из пропозициональных переменных: a, b, c₉₉ , d₃₄₅ , … , объектных переменных: x, y, z₉₉ , t₃₄₅ , … , логических связок: , ,  ,  ,  , предикатных символов: P⁽¹⁾( _ ), Q⁽¹⁾( _ ), … , P⁽²⁾( _ , _ ), Q⁽²⁾( _ , _ ), … , кванторов:  ,  и служебных символов: , и ( , ) .

Правила построения формул исчисления предикатов известны:

(Ф1): любая формула исчисления высказываний (от пропозициональных переменных) является формулой исчисления предикатов, в которой нет объектных переменных и кванторов. В этой формуле нет вхождений объектных переменных.

(Ф2): если P⁽ⁿ⁾( _ , … , _ ) – предикатный символ от n переменных и x₁ , … , x_n – объектные переменные, то P⁽ⁿ⁾( x₁ , … , x_n ) – формула исчисления предикатов, в которой все вхождения объектных переменных x₁ , … , x_n свободны, а вхождений других объектных переменных нет.

(Ф3): если A и В – две формулы, то (A  B), (A  B), (A  B), (A  B), – тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.

(Ф4): если A(x) – формула хотя бы с одним свободным вхождением объектной переменной x, то выражения ( x A(x)) и ( x A(x)) – формулы, в которых связаны вхождения всех объектных переменных, связанных в А, а также все вхождения x, и свободны все вхождения объектных переменных, свободные в А, кроме переменной х. При этом формула A(x) называется областью действия квантора.

(Ф5): других формул нет.

Аксиомы формального исчисления предикатов получаются добавлением ко всем аксиомам формального исчисления высказываний ещё одной группы схем аксиом с кванторами:

Группа аксиом с кванторами:

(): ( x А(x))  А(t) , (): А(t)  (  x А(x))

Здесь t – переменная, отличная от переменной x.

Таким образом, получается 13 схем аксиом, которые на самом деле представляют бесконечное количество аксиом.

Правила вывода в формальном исчислении предикатов:

(MP): ,