Глава II. Алгебра предикатов

§ 1. Предикаты и кванторы

Каждая наука имеет дело со специфическими объектами, совокупность которых образует объектную (или предметную) область данной науки. Об этих объектах можно формулировать высказывания, которые могут быть истинными или ложными. При этом удобно использовать не одиночные высказывания, а “высказывания” с переменными, вместо которых можно подставлять те или иные конкретные объекты.

Примеры: 1. Высказывание “Волга впадает в Каспийское море” является истинным и говорит об одной конкретной реке Волге. Можно рассмотреть следующее “высказывание” с переменной x : “Река x впадает в Каспийское море”, которое позволяет вместо переменной x подставлять любую реку и получать осмысленные высказывания. Например, при x = Иртыш получим ложное высказывание.

2. “3 – простое число” – истинное высказывание об одном числе 3, а “y – простое число” – это “высказывание с переменной” y, вместо которой можно подставлять любые целые числа и получать осмысленные высказывания. Например, при y = 17 получим истинное высказывание, а при y = 6, –7 – ложные.

Точно так же можно образовывать “высказывания ” и от нескольких переменных. Например, “x > y” – “высказывание” от двух переменных x и y, вместо которых можно подставлять любые действительные числа, “x² + y² = z² ” – “высказывание” от трёх переменных x, y и z, принимающих числовые значения.

Пусть А – произвольное непустое множество, x₁ , … , x_n – переменные. Повествовательное предложение, в котором участвуют переменные x₁ , … , x_n , обращающееся в высказывание при подстановке вместо x₁ , … , x_n произвольных элементов a₁ , … , a_n  A, называется предикатом от n переменных x₁ , … , x_n на А. Следует отметить, что для простоты будут, как правило, рассматриваться предикаты, всюду определённые на A.

Замечание: Само “повествовательное предложение, в котором участвуют переменные x₁ , … , x_n ” высказыванием не является. Например, предложение “Река x впадает в Каспийское море” бессмысленно, т.к. x – это переменная, а не название реки. Но оно становится высказыванием после подстановки вместо x произвольного названия реки.

Можно дать другое определение предиката, не ссылающееся на неопределяемое понятие высказывания: предикат P(x₁ , … , x_n) от n переменных x₁ , … , x_n на А – это произвольное отображение (т.е. всюду определённая функция) P : Aⁿ  B = {0, 1}, где значения 1 и 0 интерпретируются как обычно – истина и ложь.

Примеры: 1. “x  3” (x делится нацело на 3) – предикат от одного переменного x на Z – множестве всех целых чисел – представляет функцию P : Z  B, где P(x) = 1 тогда и только тогда, когда x делится на 3.

2. “x > ” – предикат от двух переменных x, y на A = R \ {0}, но не на R (?!). Его можно рассматривать как функцию P : AA  B двух переменных, где P(x, y) = 0 в том и только том случае, если x  .

Если P(x₁ , … , x_n) – предикат от n переменных на А, то множество D(P) = (декартово произведение n экземпляров множества А, обозначаемое также Aⁿ ) называют областью определения предиката P(x₁ , … , x_n). Множество D₁(P) = {(a₁ ; … ; a_n)  D(P) | P(a₁ , … , a_n) = 1} называют областью истинности этого предиката, а множество D₀(P) = D(P) \ D₁(P) – областью ложности предиката P(x₁ , … , x_n ). Ясно, что

D₀(P) = {(a₁ ; … ; a_n)  D(P) | P(a₁ , … , a_n) = 0}.

Сведения о простейших понятиях теории множеств даны в § 1 приложения.

Примеры: 1. Для предиката P(x) = “x  3” в соответствии с определениями

D(P) = Z, D₁(P) = {x  Z | x  3} = {… , –6, –3, 0 , 3, 6, …},

D₀(P) = Z \ D₁(P) = {… –8, –7, –5, –4, –2, –1, 1, 2, 4, 5, 7, 8, …}.

2. Для предиката P(x) = “x² > x” имеем D(P) = R, D₁(P)={x  R | x² > x} = = (–∞; 0 )  (1; +∞), D₀(P) = {x  R | x²  x} = [0; 1].

3. Для предиката P(x, y) = “x > ” получим D(P) = (R \ {0})(R \ {0}) = = (R \ {0})². Вычислим области истинности и ложности предиката:

D₁(P) = { (x; y)  D(P) | x > },D₀(P) = { (x; y)  D(P) | x  }.

Для этого решим неравенство x > :

x > > 0 y(xy – x + 1) > 0.

Е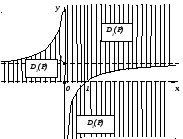слиy > 0, то xy – x + 1 > 0. Это выполнено при x = 0, при y > = 1 –(для x > 0) и при 0 < y < 1 – (для x < 0).

Для y < 0 получаем условие xy – x + 1 < 0. Это верно при y < 1 – (для x > 0).

Полученные множества D₁(P) и D₀(P) изображены на рисунке: множество D₁(P) заштриховано, а D₀(P) – нет.