Рациональные корни многочлена с целыми коэффициентами

Вопрос о нахождении рациональных корней многочлена f(x)Q[x] (с рациональными коэффициентами) сводится к вопросу об отыскании рациональных корней многочленов k ∙ f(x)Z[x] (с целыми коэффициентами). Здесь число k является наименьшим общим кратным знаменателей коэффициентов данного многочлена.

Необходимые, но не достаточные условия существования рациональных корней многочлена с целыми коэффициентами дает следующая теорема.

Теорема 6.1 (о рациональных корнях многочлена с целыми коэффициентами). Если –рациональный корень многочлена f(x) = a_n  xⁿ+ + …+ a₁  x + a₀ с целыми коэффициентами, причем (p, q) = 1, то числитель дроби p является делителем свободного члена а₀, а знаменатель q является делителем старшего коэффициента а₀.

Теорема 6.2. Если Q (где (p, q) = 1) является рациональным корнем многочлена f(x) с целыми коэффициентами, то –целые числа.

Пример. Найти все рациональные корни многочлена

f(x) = 6 x⁴ + x³ + 2 x² – 4 х+ 1.

1. По теореме 6.1: если –рациональный корень многочлена f(x), (где (p, q) = 1), то a₀ = 1 p, a_n = 6 q. Поэтому p { 1}, q{1, 2, 3, 6}, значит,

.

2. Известно, что (следствие 5.3) число а является корнем многочлена f(x) тогда и только тогда, когда f(x) делится на (х – а).

Следовательно, для проверки того, являются ли числа 1 и –1 корнями многочлена f(x) можно воспользоваться схемой Горнера:

	6	1	2	– 4	1
1	6	7	9	5	6
– 1	6	– 5	7	–11	12

f(1) = 60,f(–1) = 120, поэтому 1 и –1 не являются корнями многочленаf(x).

3. Чтобы отсеять часть оставшихся чисел , воспользуемся теоремой 6.2. Если выраженияилипринимает целые значения для соответствующих значений числителяp и знаменателя q, то в соответствующих клетках таблицы (см. ниже) будем писать букву “ц”, в противном случае – “др”.

=	ц	ц	ц	др	др	др
=	ц	ц	ц	ц	др	др

4. С помощью схемы Горнера проверяем, будут ли оставшиеся после отсеивания числа корнямиf(x). Вначале разделим f(x) на (х – ).

	6	1	2	– 4	1
	6	4	4	–2	0

В результате имеем: f(x) = (х – )(6 x³ + 4 x² + 4 х – 2) и – кореньf(x). Частное q(x) = 6 x³ + 4 x² + 4 х – 2 разделим на (х + ).

	6	1	2	– 4	1
–	6	–2	3	–5	3

Так как q (–) = 30, то (–) не является корнем многочленаq(x), а значит и многочлена f(x).

Наконец, разделим многочлен q(x) = 6 x³ + 4 x² + + 4 х – 2 на (х – ).

	6	1	2	– 4	1
	6	3	3	–3	0

Получили: q () = 0, т.е.– кореньq(x), а значит, – кореньf (x). Таким образом, многочлен f (x) имеет два рациональных корня: и.

Освобождение от алгебраической иррациональности в знаменателе дроби

В школьном курсе при решении некоторых типов задач на освобождение от иррациональности в знаменателе дроби достаточно домножить числитель и знаменатель дроби на число сопряженное знаменателю.

Примеры. 1. t = .

Здесь в знаменателе срабатывает формула сокращенного умножения (разность квадратов), что позволяет освободиться от иррациональности в знаменателе.

2. Освободиться от иррациональности в знаменателе дроби

t = . Выражение – неполный квадрат разности чисела = иb = 1. Воспользовавшись формулой сокращенного умножения а³ – b³= (а + b) · (a² – ab + b²), можно определить множитель m = (а + b) = + 1, на который следует домножать числитель и знаменатель дробиt, чтобы избавиться от иррациональности в знаменателе дроби t. Таким образом,

t = .

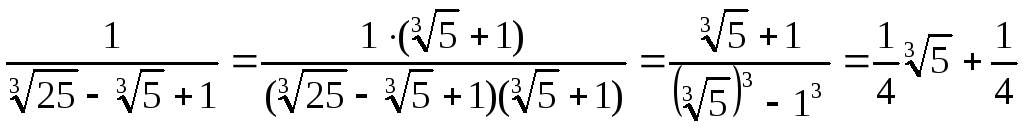В ситуациях, где формулы сокращенного умножения не работают, можно использовать другие приемы. Ниже будет сформулирована теорема, доказательство которой, в частности, позволяет найти алгоритм освобождения от иррациональности в знаменателе дроби в более сложных ситуациях.

Определение 6.1. Число z называется алгебраическим над полем F, если существует многочлен f(x) F[x], корнем которого является z, в противном случае число z называется трансцендентным над полем F.

Определение 6.2. Степенью алгебраического над полем F числа z называется степень неприводимого над полем F многочлена p(x)F[x], корнем которого является число z.

Пример. Покажем, что число z = является алгебраическим над полемQ и найдем его степень.

Найдем неприводимый над полем Q многочлен p(х), корнем которого является x = . Возведем обе части равенстваx = в четвертую степень, получимх⁴ = 2 или х⁴ – 2 = 0. Итак, p(х) = х⁴ – 2, а степень числа z равна deg p(х) = 4.

Теорема 6.3 (об освобождении от алгебраической иррациональности в знаменателе дроби). Пусть z – алгебраическое число над полем F степени n. Выражение вида t = ,где f(x), (x)F[x], (z)0

единственным образом может быть представлено в виде:

t = с_n-1 z^n-1 + c_n-2 z^n-2 + … + c₁ z + c₀, c_i F.

Алгоритм освобождения от иррациональности в знаменателе дроби продемонстрируем на конкретном примере.

Пример. Освободиться от иррациональности в знаменателе дроби:

t =

1. Знаменателем дроби является значение многочлена (х) = х² – х +1 при х = . В предыдущем примере показано, что– алгебраическое число над полемQ степени 4, так как оно является корнем неприводимого над Q многочлена p(х) = х⁴ – 2.

2. Найдем линейное разложение НОД ((х), p(x)) с помощью алгоритма Евклида.

_ x⁴ – 2 | x² – x + 1

x⁴– x³+ x² x² + x = q₁(x)

_ x³– x² – 2

x³– x²+ x

x² – x + 1 | – x –2 = r₁ (x)

x² + 2x – x + 3 = q₂(x)

_–3x + 1

–3x – 6

_ – x –2 |7 = r₂

– x –2 -x - =q₃(x)

0

Итак, НОД ((х), p(x)) = r₂ = 7. Найдем его линейное разложение.

Запишем последовательность Евклида, пользуясь обозначениями многочленов.

p(x) = (x) · q₁(x) + r₁(x) r₁(x) = p(x) – (x) · q₁(x)

(x) = r₁(x) · q₂(x) + r₂(x) r₂(x) = (x) – r₁(x) · q₂(x)

r₁(x) = r₂(x) · q₂(x).

Подставим в равенство 7= r₂(x) = (x) – r₁(x) · q₂(x) значение остатка r₁(x) = p(x) – (x) · q₁(x), после преобразований получим линейное разложение НОД((х), p(x)): 7 = p(x) · (– q₂(x)) + (x) · [1 + q₁(x) · q₂(x)]. Если подставить в последнее равенство вместо обозначений соответствующие многочлены и учесть, что p() = 0, то имеем:

(1 – +) · (–+ 2+ 3+ 1)] = 7 (1)

3. Из равенства (1) следует, что если знаменатель дроби t умножить на число m = [1 + (– + 2+ 3+ 1)], то получим 7. Таким образом,

t = =.

МЕТОДИКА 16. Тема урока: Стандартный вид многочлена

Класс: 7

Тип урока: урок проверки и контроля знаний и умений

Цели урока:

- проверить умения приводить многочлен к стандартному виду

- развивать у учащихся логическое мышление, внимание

- воспитывать самостоятельность

Структура урока:

1. Организационный момент

2. Инструктаж

3. Самостоятельная работа.

Задания:

1. Дополните предложения:

а) Выражение, содержащее сумму одночленов называют …(многочленом).

б) Многочлен состоящий из стандартных одночленов и не содержащий подобных слагаемых называется … (стандартным многочленом).

в) Наибольшую из степеней одночленов входящих в многочлен стандартного вида называют … (степенью многочлена).

г) Прежде чем определить степень многочлена, нужно … (привести его к стандартному виду).

д) Для нахождения значения многочлена нужно сделать первое…(представить многочлен в стандартном виде), второе …(подставить значение переменной в данное выражение).

2. Найти значение многочлена:

а) 2a⁴-ab+2b²приa=-1, b=-0,5

б) x²+2xy+y²приx=1,2, y=-1,2

3. Привести многочлен к стандартному виду:

а) -5ах² + 7а²х + 2а²х + 9ах² – 4ах² – 8а²х;

б) (5х² – 7х – 13) – (3х² – 8х + 17);

в) 2а – (1,4ав + 2а² – 1) + (3а + 6,4ав);

г) (2с² – 1,6с + 4) – ((10,6с² + 4,4с – 0,3) – (3,6с² – 7с – 0,7));

4. Привести многочлен к стандартному виду и выяснить при каких значениях хего значение равно 1:

а) 2x²-3x-x²-5+2x-x²+10;

б) 0,3x³-x²+x-x³+3x²+0,7x³-2x²+0,07

Билет № 17. Делимость целых чисел