23. Часова когерентність

Випромінювання окремого атома, який належить до деякої сукупності збуджених частинок, описується квазігармонічною функцією такого типу 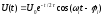, причому всі параметри процесу – амплітуда , частота,фаза поляризація - у кожному окремому випадку є випадковими величинами. У відповідності з принципом суперпозиції результуюче полевипромінювання ансамблю однакових частинок, яке виявляється у довільній точці просторуP , є векторною сумою всіх діючих полів

(4.1)

Тут, - функція Хевісайда, всі стосуються минулого часу відносно моменту спостереження. Фаза кожного коливання, яке дійшло до точки спостереження, визначається початковою фазою та запізненням внаслідок пробігу певної відстані. У загальному випадку випромінювання від декількох не- однотипних атомів, яке досягло точки з координатами, вносить у сумарне поле у цій точці невизначеність за всіма параметрами – частотою, амплітудою, поляризацією. Відстані між випромінювачами і точ- кою спостереження у конкретній реалізації є певним набором, однак розподіл величин у цьому наборі має випадковий характер. Таким чином, оптичне збудження від природного джерела у будь-якій точці простору можна розглядати як випадковий процес.

Друга важлива обставина: довільний оптичний приймач реагує не нa напруженість поля, а на енергію (потужність) світлового потоку. Більше того, його реакція відноситься до певного проміжку часу усере-

днення. Навіть дуже коротку дію він перетворює у сигнал обмеженої тривалості, яку не можна зменшити. Цей сигнал не можна також приписати якомусь певному моменту часу у межах дуже короткої дії. Між енергією світлової хвилі, яка падає на приймач, і від- гуком (його електричним сигналом, підвищенням температури, механічним розширенням, взагалі - реакцією приймача на світло) є, взагалі кажучи, деяка кореляція, але не однозначний зв’язок. Сферична хвиля, поглинута конкретним електроном (атомом), зникає миттєво у всьому просторі, тому що фотон не- скінченний, існує у всіх точках простору одночасно, хоча і з різною ймовірністю. А максимум її переміщується зі швидкістю с. Але електрон (атом) також нескінченний. Тому взаємодія проходить у всьому нескінченному об’ємі одночасно, а результат (реакція) локально проявляється у випадковий момент часу. У такій інтерпретації саме переміщення максимальної ймовірності можливої взаємодії хвилі з електричними зарядами і є швидкість світла.

Для вивчення і достовірного опису світлових полів у таких умовах найбільш плідним виявився метод, який ґрунтується на визначенні ступеня узгодженості, ко- реляції полів у різних просторово-часових точках. Він цілком задовільно описує не лише хвильові процеси, але і корпускулярні прояви (і властивості) світлових полів.

Дослідження кореляції – є більш поширеним занят- тям, ніж прийнято вважати. Будь-яка пізнавальна діяльність (тобто, одержання і класифікація інформа- ції) носить кореляційний характер. Модуль числового значення кореляції змінюється у межах [01], тобто, від відсутності її до повної (абсолютної) відповідності, кореляції. Останній випадок прийнято називати нау- ковим законом, якщо відповідна кореляція має суттєві наслідки, тобто, мова йде про фундаментальні зв’язки між явищами, наприклад: закони Ньютона

Ома, Ленца і т.д. Соціометрія вивчає ступінь кореля- ції між явищами суспільного життя у різних умовах, біометрія - вплив різних факторів, які можна контро- лювати, на розвиток біоорганізмів. Є кореляція між числом Вольфа (кількість темних плям на Сонці) і час- тотою аварій на транспорті, хоча про фізичний механізм такого зв’язку можна лише здогадуватися. По суті будь-яка наука починається із встановлення кореляції між суб’єктивно вибраними явищами. Фак- тор суб’єктивності (інтуїція), як правило, економить час і засоби при пошуку кореляції: шукають не де за- вгодно, а там, де це, як нам здається, має сенс. Однак іноді і цей досвід підводить: психологічно важко примусити себе шукати те, що ні на що не схоже. Революційні знахідки і розв’язки у науці хара- ктеризуються абсолютною несхожістю на попередні. Природно, пошук може бути приречений на невдачу через помилкову гіпотезу. Наприклад, побутує пере- конання, що існує телепатичний канал передачі інформації, є достатньо переконливі експерименти, проте вхопити суть явища при сучасному науково- методичному підході не вдається. Сотні років людст- во спостерігало електричні явища, не знаючи, як до них підступитись, поки Л.Гальвані (Luigi Galvani,1737-1798) випадково не помітив (1786) див- ну поведінку жаб’ячих лапок (чи то при розрядах блискавки, чи то при простому дотику дротиною). А. Вольта (Alessandro Giuseppe Antonio Anastasio Volta, 1745-1827) пояснив, що це означає, і винайшов електричну батарею (не так давно, у рік народження Дж. Вашингтона і А. Пушкіна, 1799). Яке це мало продовження для науки, світогляду і практики - мо- жна поцікавитись у інтернеті.

Функція кореляції. Величину електромагнітного (світлового) поля поки що неможливо виміряти у дові- льній точці у заданий момент. Тому таке завдання і

не ставиться, натомість вводиться функція кореляції між полями i у різних просторовочасових позиціях, а також поняття когерентності. Практично під когерентністю першого порядку розу- міється, у кінцевому підсумку, здатність різних полівI утворювати стійку інтерференційну картину (ІК), а кількісно вона визначається як функція взаємної кореляції:

(4.2)

Тут - часовий зсув між моментами спостереження досліджуваних функцій, - функція взаємної когерентності або взаємна енергія сигналіві, це загальний її вигляд. Формально,– це енергія поля у точці Часова когерентність полів розглядається, як правило, у деякій точці, вираз (4.2) виглядає простіше. Іноді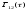визначається як

, (4.3)

яка у цьому випадку називається взаємною середньою потужністю сигналів. Слід мати на увазі, що у випадку обмежених у часі функцій інтервал інтегрування практично не повинен виходити за межі перекриття функцій і , бо інакшебуде втрачати інформативність, наприклад, прямуючи до нуля для реальних функцій при.Частіше використовується нормована функція взаємної когерентності

(4.4)

яка і називається ступінню кореляції або комплекс- ною ступінню когерентності. Як відмічалось раніше,

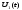і – це енергетична величина, пропорційна інтенсивності світла іу точці . Межі інтегрування при визначення;;; повинні бути однаковими і не більшими області існування і перекриття функцій і .

Розрізняють як мінімум два типи когерентності: часову і просторову. Перша характеризує джерело зі сторони спектрального складу випромінювання, ступінь його монохроматичності, на використанні цієї функції базується фур’є-спектроскопія. Друга описує його властивості у просторі, є функцією координат і, як наслідок, характеризується спектром просторових частот, і пов’язана із фур’є-оптикою.

Рис. 4.1. Схема для спостереження двопроменевої інтерференції

Часова когерентність і видність ІК. Розглянемо експеримент, схема якого приведена на рис. 4.1. Монохроматичне світло від точкового джерела досягає екранудвома шляхами і створює на ньому ІК. Різниця ходу для центральних променів 1 і 2 дорівнює , що відповідає запізненню на . Для будь яких нецентральних променів різниця ходу буде ін- шою, тому і спостерігається ІК у площині .

Результуюча напруженість поля дорівнює

(4.5)

інтенсивність світла у точці спостереження визначається як

(4.6)

Тому

(4.7)

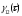–нормована функція взаємної когерентності (4.4)– величина комплексна, (c – швидкість світла, - довжина хвилі).Контраст V визначаємо, як завжди, за пропозицією Майкельсона

(4.8)

де – інтенсивність світла у екстремумах світлої і темної інтерференційних смуг відповідно (у області нульової смуги ІК!). Максимальний контраст можна отримати, якщо використовувати хвилі однакової інтенсивності Враховуючи, що , то

,

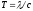
бо положення світлої і темної смуг у ІК зумовлено значенням різниці ходу відповідно або,та значенняміОтже, контраст ІК (4.8) із врахуванням (4.9) дорівнює

(4.10)

Таким чином, змінюючи затримку τ одного проме- ня відносно іншого і вимірюючи величину контрасту ІК V , тим самим вимірюємо модуль функції автоко- реляції випромінювання , обто, часову когерентність випромінювання даного точкового джерела(рис. 4.1). Якщо

, що може бути при

використанні у схемі рис. 4.1 дзеркал з довільними параметрами, то із (4.8) – (4.10) одержуємо кількісний зв’язок між контрастом ІК і функцією автокореляції

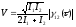(4.11)

Природньо, величининеобхідно якимось чином попередньо визначити. Діапазон зміни модуля функції автокореляціїміститься у межах [0,1]. Природа самої часової когерентності зумовлена, зокрема, обмеженим часом актів випромінювання атомних систем і, як наслідок цього, немонохроматичністю випромінювання (див. нижче). У загальному випадку розширення спектру випромінювання внаслідок будь-якої причини неминуче приводить до скорочення часу когерентності - це випливає з теореми Вінера-Хінчина.

На закінчення нагадаємо: єдиним критерієм (і спосо бом визначення) ступеня часової когерентності випромінювання точкового джерела є здатність утворювати контрастну ІК при різній взаємній затримці інтерферуючих хвиль, одержаних від цього точкового джерела. Контраст (видність) ІК є коефіцієнтом автокореляції випромінювання точкового джерела (формула (4.10)).

Розглянемо як приклад функцію часової когерентності для дипольного випромінювання, яке відбувається із затуханням :

, (4.12)

де – функція Хевісайда.

Обчислимо інтеграл:

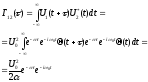(4.13)

Хоч функція виникає при, інтегрування у (4.13) ведеться починаючи із, що зумовлено другою функцією Хевісайда. Зокрема,

(4.14)

Функція кореляції (4.13) у цьому випадку характеризує функцію випромінювання і називається автокореляцією.

це періодична спадаюча із зростанням затримки комплексна функція.

Прийнято вважати, що когерентність зберігається протягом часу , тобто, в межах зменшення функціївраз, причому виявляється, що ширина спектральної лінії випромінюванняна половині висоти (напівширина) дорівнює 2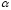. Множникзабезпечує швидку зміну інтенсивності у ІК (наявність смуг), а- власне залежність ко реляції від запізнення.

Для дійсних функцій автокореляція у нулі має максимальне значення, тому сплеск інтенсивності у нульовому максимумі у всіх ІК найбільший. Розглянемо очевидне твер-дження

(4.16)

де можна представити - довільне дійсне число.

Розкриємо його для випадку

(4.17)

тобто, автокореляція дійсних функцій ніде не пере- вищує свого значення у нулі:

(4.18)

Крім того, для дійсних функцій вона симетрична відносно точки

(4.19)

що видно при заміні під інтегралом (4.19). На

рис. 4.2 наведено кілька прикладів ІК, які отримані за допомо-гою інтерферометра Жамена, для випромінювання різного сту-пеня монохроматичності: лампи розжарення (ЛР) (та), Р зі світлофільтром ОС-11 (б), ЛР з інтерференційним ільтром (в). Записи (окрім) зроблені при однаковій швидкості розго-ртки. Діючий спектр обмежується також і спектральною чу-тливістю фотокатода ФЭУ-68.

Можна зробити висновок, що функція автокореля- ції однозначно зв’язана із спектральним складом і цей зв’язок можна використати для спектрального аналізу. Відповідна наука називається фур’є-спектроскопією. Як приклад, на рис. 4.3 показано отриману

Рис. 4.2. Інтерферограми випромінювання джерел з різною шириною спектра: ЛР (;), ЛР зі світлофільтром ОС-11 (б), ЛР з інтерференційним фільтром (в).

Рис. 4.3. Фрагмент інтерферограми випромінювання ртутної лампи, видима область.

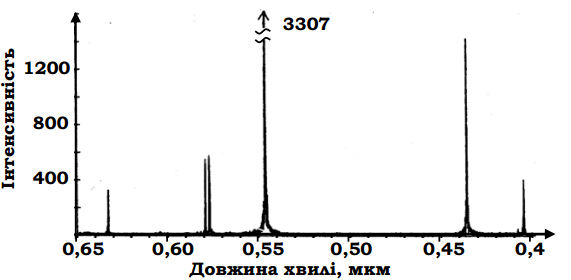
Рис. 4.4. Спектр ртуті, одержаний у результаті вико- нання ПФ над інтерферограмою рис. 4.3.

за допомогою двопроменевого інтерферометра Май- кельсона інтерферограму (фрагмент) випромінювання ртутної лампи (видима область). Спектр ртуті, одер- жаний у результаті виконання ПФ над записаною інтерферограмою, наведено на рис. 4.4. Як еталон довжини при обчисленні переміщення дзеркала ін- терферометра використовувалась лінія 0,633 мкм гелій-неонового лазера.

Довжина когерентності - це відстань, яку проходить хвиля за час:

,

у випадку дипольного випромінювання – це довжина цуга, відстань, яку пройшла хвиля, зменшивши напруженість у е разів.

Для вивчення часової когерентності можна вико- ристовувати будь-який інтерферометр, який забезпечує потрібне запізнення . Джерело, яке вивчається, повинно бути точковим (для уникнення впливу просторової когерентності на результат виміру). На рис. 4.5 та рис. 4.6 наведено приклади фрагментів записів інтерферограм, отриманих за допомогою ін- терферометра Жамена, при виділенні із випромінювання ртуті жовтого дублетумкм,мкм та жовтого дублету і зеленої лінії.