
- •Пояснювальна записка
- •Розділ 1. Матриці та вектори
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця.
- •Контрольні запитання
- •Тема 2. Системи лінійних рівнянь
- •Контрольні запитання
- •Тема 3. Довільні системи лінійних рівнянь
- •Контрольні запитання
- •Тема 4. Елементи векторної алгебри
- •Контрольні запитання
- •Розділ 2. Основи аналітичної геометрії
- •Тема 5. Пряма лінія на площині
- •Контрольні запитання
- •Тема 6. Криві другого порядку
- •Контрольні запитання
- •Тема 7. Площина та її рівняння
- •Видно, що ,( тобто площина паралельна до осіOx.
- •4. Кут між двома площинами.
- •Нехай маємо площину задану нормальним рівнянням
- •Контрольні запитання
- •Тема 8. Пряма в просторі
- •Контрольні запитання
- •Розділ 3. Вступ до математичного аналізу Тема 9. Функція та її границя. Основні теореми про границю.
- •Контрольні запитання
- •Тема 10. Неперервність функції в точці
- •Контрольні запитання
- •Контрольні запитання
- •Тема 12. Диференціал функції. Похідні вищих порядків
- •Контрольні запитання
- •Тема 13. Дослідження функцій за допомогою похідної
- •Контрольні запитання
- •Розділ 5. Функції багатьох змінних
- •Тема 14. Границя функції багатьох змінних
- •Контрольні запитання
- •Тема 15. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних
- •Контрольні запитання
- •Розділ 6. Інтегрування функції однієї змінної
- •Тема 16. Первісна функція та неозначений інтеграл
- •3. Таблиця основних інтегралів
- •Контрольні запитання
- •Тема 17. Визначений інтеграл та його обчислення
- •Скориставшись цим, маємо
- •Таким чином
- •Розв’язування. В силу симетрії кривої визначаєм спочатку одну чверть шуканої площі
- •Контрольні запитання
- •Розділ 7. Звичайні диференціальні рівняння
- •Тема 19. Поняття про диференціальні рівняння, рівняння з відокремлюваними змінними
- •Основна задача теорії інтегрування диференціальних рівнянь
- •Контрольні запитання
- •Тема 20. Диференціальні рівняння 1-го порядку
- •Диференціальне рівняння
- •Контрольні запитання
- •Тема 21. Лінійні диференціальні рівняння n-го порядку з постійними коефіцієнтами
- •Контрольні запитання
- •Перелік рекомендованої літератури
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця 4с.
4. Кут між двома площинами.
Нехай
задано дві площини А1х+В1y+C1z+D1=0
і А2х+В2y+C2z+D2=0.
Знайдемо кут між цими площинами. Так як
кут між площинами рівний кутові між їх
нормальними векторами, то досить лише
знайти кут між векторами
![]() та
та![]() .
Тобто
.
Тобто
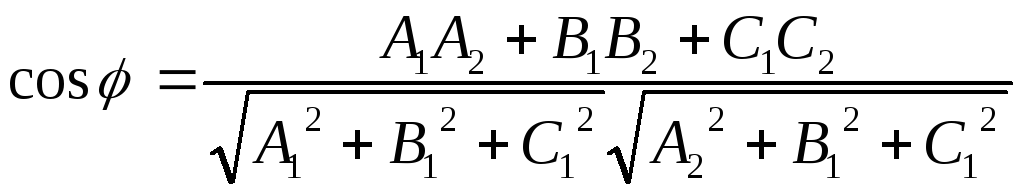 (1)
(1)
З формули (4) випливає необхідна і достатня умова паралельності двох площин
![]()
та перпендикулярності площин
![]() .
.
Відстань від точки до площини.
Нехай маємо площину задану нормальним рівнянням
![]()
і
деяку точку
![]()
![]() .
.
Аналогічно
до випадку відстанні від точки до прямої
можна показати, що
![]() .
.
Якщо площина задана загальним рівнянням, то
![]()
![]() .
.
Контрольні запитання
Що називається рівнянням поверхні?
Доведіть теорему про загальне рівняння площини.
Як записати рівняння площини, що проходить через три точки?
Виведіть нормальне рівняння площини.
Як обрахувати кут між площинами?
Як обрахувати відстань від точки до площини?
Тема 8. Пряма в просторі
Мета. Поширити поняття про пряму як лінію в просторі. Розглянути різні види рівняння прямої, порівняти їх з відповідними рівняннями прямої на площині.
План.
Поняття про рівняння лінії в просторі.
Загальне рівняння прямої. Пучок площин.
Канонічне рівняння прямої. Рівняння прямої, що проходить через дві задані точки.
Кут між двома прямими, кут між площиною і прямою.
1. Нехай маємо в просторі дві поверхні, що перетинаються. Рівняння однієї поверхні запишемо F1 (x,y,z)=0 , а другої поверхні F2 (x,y,z)=0. Усі точки лінії перетину двох поверхонь задовільняють як перше так і друге рівняння. Таким чином рівняння отриманої лінії запишемо у вигляді:

Наприклад,

Крім того, лінію в просторі можна задати параметрично як вирази трьох функцій (абсциси, ординати і аплікати) відносно деякого параметра t.

2. Так як пряма є лінією перетину двох площин, то загальне рівняння прямої в просторі можна задати у вигляді:
 (1)
(1)
Коефіцієнти A1, B1, C1, A2, B2, C2 не є пропорційними.
Розглянемо поняття пучка площин.
Нехай
 -
деяка пряма в просторі.
-
деяка пряма в просторі.
Пучком площин називається сукупність площин, які проходять через дану пряму. Пряма в такому випадку називається віссю пучка.
При довільному рівняння виду
![]() (2)
(2)
визначає площину.
Приклад. Скласти рівняння пучка площин, який проходить через пряму
 і
точку M(2;1;1).
і
точку M(2;1;1).
Розв’язання.
x-3y+z+2+(x-y-3z-2)=0,
2+3+1+2+(2-1-3-2)=0,
8-4=0,
=2.
x-3y+z+2+2(x-y-3z-2)=0,
3x+y-5z-2=0.
3.
Нехай задано
точку М1(х1,
y1,
z1)
, що належить прямій і вектор
![]() напрямний
до неї. Виберемо довільну точку М(x,y,z)
цієї прямої. Аналогічно до рівняння
прямої на площині маємо, що
напрямний
до неї. Виберемо довільну точку М(x,y,z)
цієї прямої. Аналогічно до рівняння
прямої на площині маємо, що
![]() колінеарний
вектору
колінеарний
вектору
![]() За
ознакою колінеарності
За
ознакою колінеарності
![]()
Це рівняння називають канонічними рівняннями прямої. Взявши t – параметр колінеарності, маємо

Отримали параметричне рівняння прямої з параметром t.
Нехай
задано точки M
1
(x1,
y1,
z1)
та
М2
(x2,
y2,
z2)
, що
належать площині тоді вектор
![]() напрямний до неї. Виберемо довільну
точкуМ(x,y,z)
цієї прямої. Використовуючи канонічне
рівняння прямої маємо
напрямний до неї. Виберемо довільну
точкуМ(x,y,z)
цієї прямої. Використовуючи канонічне
рівняння прямої маємо
![]()
Для того, щоб звести загальне рівняння до канонічного виду потрібно:
Знайти координати деякої точки М, що належить прямій, враховуючи, що точка перетину прямої і координатної площини має одну координату рівну нулеві, а дві інші однозначно визначаються з загального рівняння.
Знайти напрямний вектор прямої, обчисливши його координати як координати векторного добутку двох векторів нормалей до площин, рівняння яких записанні в загальному рівнянні прямої.
Записати рівняння прямої через точку та напрямний вектор.
4. Нехай кут є кутом між двома прямими, зрозуміло, що він дорівнює кутові між напрямними векторами цих прямих.
Якщо прямі заданні канонічними рівняннями і їх напрямні вектори (l1,m1,n1) та (l2,m2,n2), то косинус кута ( можна обраховувати використовуючи означення скалярного добутку
![]()
Умови паралельності і перпендикулярності прямих аналогічні до прямих на площині
Для того, щоб знайти кут між прямою і площиною, врахуємо, що sin=cos, де кут - кут між прямою та площиною (чи, що те саме, що й кут між прямою та її проекцією) , а - кут між нормальним вектором площини та напрямним вектором прямої.
Тобто,
![]()
