
- •Пояснювальна записка
- •Розділ 1. Матриці та вектори
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця.
- •Контрольні запитання
- •Тема 2. Системи лінійних рівнянь
- •Контрольні запитання
- •Тема 3. Довільні системи лінійних рівнянь
- •Контрольні запитання
- •Тема 4. Елементи векторної алгебри
- •Контрольні запитання
- •Розділ 2. Основи аналітичної геометрії
- •Тема 5. Пряма лінія на площині
- •Контрольні запитання
- •Тема 6. Криві другого порядку
- •Контрольні запитання
- •Тема 7. Площина та її рівняння
- •Видно, що ,( тобто площина паралельна до осіOx.
- •4. Кут між двома площинами.
- •Нехай маємо площину задану нормальним рівнянням
- •Контрольні запитання
- •Тема 8. Пряма в просторі
- •Контрольні запитання
- •Розділ 3. Вступ до математичного аналізу Тема 9. Функція та її границя. Основні теореми про границю.
- •Контрольні запитання
- •Тема 10. Неперервність функції в точці
- •Контрольні запитання
- •Контрольні запитання
- •Тема 12. Диференціал функції. Похідні вищих порядків
- •Контрольні запитання
- •Тема 13. Дослідження функцій за допомогою похідної
- •Контрольні запитання
- •Розділ 5. Функції багатьох змінних
- •Тема 14. Границя функції багатьох змінних
- •Контрольні запитання
- •Тема 15. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних
- •Контрольні запитання
- •Розділ 6. Інтегрування функції однієї змінної
- •Тема 16. Первісна функція та неозначений інтеграл
- •3. Таблиця основних інтегралів
- •Контрольні запитання
- •Тема 17. Визначений інтеграл та його обчислення
- •Скориставшись цим, маємо
- •Таким чином
- •Розв’язування. В силу симетрії кривої визначаєм спочатку одну чверть шуканої площі
- •Контрольні запитання
- •Розділ 7. Звичайні диференціальні рівняння
- •Тема 19. Поняття про диференціальні рівняння, рівняння з відокремлюваними змінними
- •Основна задача теорії інтегрування диференціальних рівнянь
- •Контрольні запитання
- •Тема 20. Диференціальні рівняння 1-го порядку
- •Диференціальне рівняння
- •Контрольні запитання
- •Тема 21. Лінійні диференціальні рівняння n-го порядку з постійними коефіцієнтами
- •Контрольні запитання
- •Перелік рекомендованої літератури
- •Тема 1. Матриці та визначники. Мінори. Обернена матриця 4с.
3. Таблиця основних інтегралів
Кожна формула з таблиці похідних має відповідну формулу в таблиці інтегралів.
 .
7.
.
7.
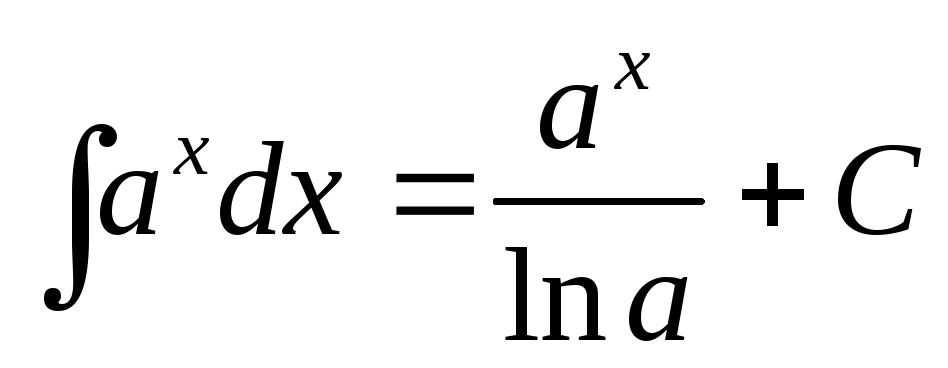 .
. .
8.
.
8.
 .
. .
9.
.
9.
 .
. .
10.
.
10.
 .
. .
11.
.
11.
 .
. .
12.
.
12.
 .
.
Додатково варто знати формули
13.
![]() .
14.
.
14.![]() .
.
15.
![]() .
16.
.
16.![]() .
.
Правильність усіх формул перевіряється диференціюванням їх правих частин.
Є три основні методи інтегрування функцій: метод розкладу, метод заміни змінної та метод інтегрування за частинами.
Метод розкладу.
Справедливі наступні твердження.
Теорема
1.
Якщо функції
![]() мають
первісні на проміжку(a,b),
то на цьому проміжку мають первісну і
функції
мають
первісні на проміжку(a,b),
то на цьому проміжку мають первісну і
функції
![]() і
справедлива рівність:
і
справедлива рівність:
![]() (1)
(1)
Теорема
2.
Якщо функція
![]() має
первісну на проміжку(a,b),
то на цьому проміжку має первісну і
функція
має
первісну на проміжку(a,b),
то на цьому проміжку має первісну і
функція
![]() і
справедлива рівність:
і
справедлива рівність:
![]() ,
k0
(2)
,
k0
(2)
Наслідок.
Якщо функції
![]() мають
первісні на проміжку(a,b),
то на цьому проміжку мають первісну і
функції
мають
первісні на проміжку(a,b),
то на цьому проміжку мають первісну і
функції
![]() і справедлива рівність:
і справедлива рівність:
![]() (3)
(3)
Метод інтегрування з використанням теорем 1,2 та наслідку називають методом розкладу.
Метод заміни змінної.
Теорема 3. Якщо F(x) – первісна для функції f(x) на проміжку (a, b) і якщо функція x=(x) диференційована на проміжку (, ), причому складена функція F((t)) визначена на проміжку (, ), то функція f( (t))’(t) на проміжку (, ) має первісну, причому
![]() .
(4)
.
(4)
Метод інтегрування за допомогою теореми 3 називається методом інтегрування способом заміни змінної.
Приклад.
![]()
Метод інтегрування частинами.
Теорема
4.
Якщо
функції
![]() диференційовні
на
проміжку
(a,b)
і на цьому проміжку існує первісна для
функції
диференційовні
на
проміжку
(a,b)
і на цьому проміжку існує первісна для
функції
![]() ,
то на проміжку(a,
b)
існує
первісна і для функції
,
то на проміжку(a,
b)
існує
первісна і для функції
![]() і
має місце рівність
і
має місце рівність
![]() .
(5)
.
(5)
До
правої частини ми не додали довільної
сталої С,
оскільки така стала міститься в іннтегралі
![]() .
.
Формула (5) називається формулою інтегрування частинами, а метод інтегрування, що грунтується нга ній – методом інтегрування частинами.
Розглянемо приклад.
![]() ,
,
позначивши
![]() ,
отримаємо
,
отримаємо
![]() .
.
Деколи цю формулу птрібно застосовувати декілька разів.
![]()
![]() .
.
Попутно зауважимо, що для обчислення більшості інтегралів потрібно, як правило, застосовувати різні методи.
Контрольні запитання
Що називається первісною?
Які функції мають первісні?
Скільки первісних має функція?
Як знайти всі первісні?
Що називається невизначеним інтегралом?
Сформулюйте і доведіть його властивості.
Чому рівні інтеграли від основних функцій?
У чому полягає інтегрування методом розкладу ?
У чому полягає інтегрування методом заміни змінної ?
У чому полягає метод інтегрування частинами ?
