Расчет несимметричной трехфазной цепи

Порядок расчета состоит в следующем.

1. Преобразуем исходную цепь путем преобразования «звезды» в «треугольник» или наоборот в зависимости от конкретной схемы. Для этого необходимо использовать следующие формулы.

A A

Za

Zca Zaв Zс Zв

C B C B

Zвc

Z _A = ,Zв= ,Z_С= ,

Z _АВ= Z_А+ Z _B + ,Z _BC = Z _B + Z _C + ,Z _СА= Z _C + Z _A + .

2. Так как одноименные фазы эквивалентных треугольников присоединены к одинаковым напряжениям, то их можно считать соединенными параллельно и, сложив их проводимости, получить эквивалентный треугольник.

3. Эквивалентный треугольник преобразовать в эквивалентную звезду с целью учета сопротивления линии. В результате схема с несколькими несимметричными звездами преобразуется в схему с одной несимметричной звездой.

4. Мощности рассчитываются по формулам:

S = U I* , P = Re ( U I ^*) , Q = Im (U I ^*)

5. Симметричные составляющие нулевой, прямой и обратной последовательностей определяются по формулам:

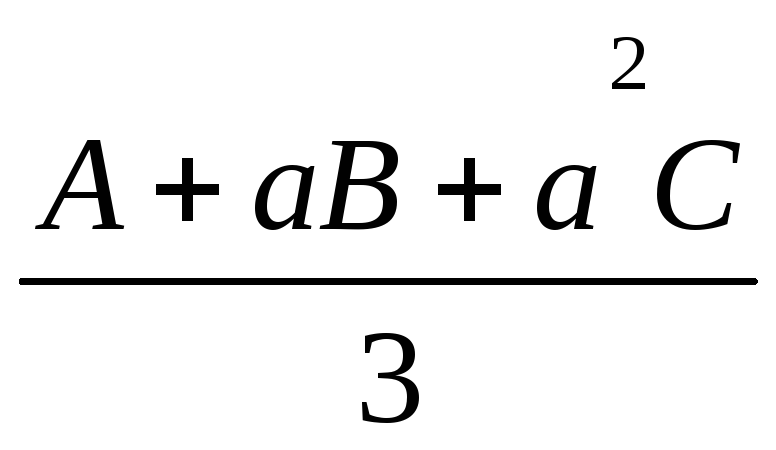А ₀ = ;А ₁ = ;А ₂ = ,

Где А, В, С – векторы несимметричной системы,

а – оператор поворота, а = е ^{j 120 o} , a² = e ^{j 240 o} .

Пример. Z1 Z3

Ia1 A1 Ia3 A2

A

Z1 Iв1 Iв3 Z3 B2

B

Z1 Ic1 C1 Ic3 Z3 C2

C

Ic2 Ia2 Iв2 Ica

Zс2 Zв2 Zca Zвс Zaв

Za2 Рисунок 1. Iaв

1. Заменим треугольник сопротивлений эквивалентной звездой и сложим сопротивления лучей звезды с сопротивлением линии Z ₃. Получим две звезды, присоединенные к точкам А ₁, В ₁, С ₁ (рис.2)

Z1

Ia1 A1

A

Z1 Iв1 B1

B

Z1 Ic1 C1

C

Ic2 Ia2 Iв2 Ic3 Ia3 Iв3

Zc2 Zв2 Zc3 Za3 Zв3

Za2

Рисунок 2.

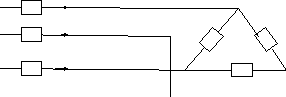
2. Преобразуем каждую звезду в эквивалентный треугольник и просуммируем проводимости одноимённых ветвей. Получим схему с одним эквивалентным треугольником (рис.3)

Z1

Ia1 A1

A

Z1 Iв1

B

Z1 Ic1 C1 B1

C

Рисунок 3.

3. Преобразуем эквивалентный треугольник в эквивалентную звезду и сложим сопротивления лучей звезды с сопротивлениями линии Z ₁ (рис.4)

Za

Ia1

A

Zв Iв1 N

B

Zс Ic1

C

Рисунок 4.

4. Получена несимметричная звезда без нейтрального провода. Найдем напряжение нейтрали:

U _N = , где Y – результирующие проводимости каждой фазы соответственно индексу.

Напряжение на фазах этой звезды:

U _A¹ = U _A – U _N ; U _B¹ = U_B – U _N; U _C¹ = U _C- U _N

5. Ток в начале линии:

I _A1 = и т.п.

6. Определим фазные напряжения на зажимах А ₁,В ₁,С ₁:

U_А1 = U _A – I_A1 Z₁ и т. п.

7.Аналогично п.4, используя U _A1, U _B1, U_C1 проводимости Y_A2, Y _B2, Y _C2, определим напряжение U _N1, а затем токи в лучах исходной звезды.

U _A1^! = U _A1 – U _N1 и т. п.

Ia2 = и т.п.

8. Линейные токи исходного треугольника можно определить также как

в п.7 или по закону Кирхгофа:

I _A3 = I _A1 – I_A2 и т.п.

9.Определим фазные и линейные напряжения на зажимах А ₂, В ₂, С ₂.

U _A2 = U _A1 - I _A3Z ₃ и т.п.

U _A2B2 = U_{А 2} – U _B2 и т.п.

10. Определим токи в треугольнике

I _AB = и т.п.

Таким образом, нам стали известны токи в любом участке схемы, что позволяет определить любую мощность.

Все расчеты производятся в комплексной форме. Целесообразнее производить умножение и деление комплексных чисел в показательной форме, а сложение и вычитание в алгебраической.

Пример 1.

22е ^{-j 120 o} *10 e ^{j 60 o}= 220e ^{j (-120 o60 o)}= 220 e ^{-j 60 o}

22е ^{-j 120 o} /10 e ^{j 60 o} = 2,2 e ^{j ( -120 o – 60 o)} = 2,2 e ^{–j 180 o}

Таким образом, при умножении комплексных чисел показатели их степеней складываются, а при делении – из показателя делимого вычитается показатель делителя. Модули соответственно перемножаются или делятся.

Пример 2.

22 е ^{– j 120 o} – 10e ^{j 60 o}

Для вычитания перейдем от показательной формы записи комплексного числа к алгебраической через тригонометрическую, используя формулу Эйлера

r e ^jj = r (cos j + j sin j), где

r – модуль комплексного числа, j - его аргумент.

22е ^{–j 120o} = 22 (cos (-120 ^o) + j sin (-120 ^o)) = 22 (cos 120 ^o – j sin 120 ^o) =

22 (-) = - 11 – j 11;

10 e ^{j 60 o} = 10 ( cos 60 ^o + j sin 60 ^o) = 10 () = 5 + j 5;

-11 – j 11 - 5 – j 5 = - 16 –j 27,7;

Переведем последнее комплексное число из алгебраической формы в показательную по формуле:

a + j b = e ^{j arctg}

-16 –j 27,7 = e^{j arctgp} = 32 e ^{j 60o - p} = 32 e ^{–j 120 o - p}

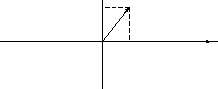
Напомним, что аргумент комплексного числаj = arctg определяется по разному в зависимости от того, в какой четверти лежит этот угол.

II j I

j = p - arctg bj = arctg

III 0 a IV 1

j = arctg j = - arctg

Величины a и b в этих формулах берутся положительными.

Исходные данные для задания 2.

1. Определить величины, указанные на каждой схеме.

2.Построить векторную диаграмму токов для D или U в зависимости от

расположения ветви, указанной на схеме и разложить ток этой части

схемы на симметричные составляющие.

Исходные данные для 2-го задания.

R	R 1	R 2	R 3	R 4	R 5	R 6	R 7	R 8	R 9
Ом	К	2К	3К	К	4К	5К	К	2К	3К

Х L	L 1	L 2	L 3	L 4	L 5	X c	C 1	C 2	C 3	C 4	C 5
Ом	К	2К	3К	К	4К	Ом	К	2К	К	2К	3К

K = pN , p = 1 для 31 группы р = 2 для 32 группы, N – номер по журналу

Для N:

1,10,19	2,11,20	3,12,21	4,13,22	5,14,23	6,15,24	7,16,25	8,17,26	9,18,27
Cx. 1	Сх.2	Сх.3	Сх.4	Сх.5	Сх.6	Сх.7	Сх.8	Сх.9

Задание 3