Многолучевая интерференция

Пусть складывается N колебаний с одинаковой амплитудой A и сдвиг фаз между которыми одинаков и равен . Тогда, как видно из векторной диаграммы,

Рисунок 13	Рисунок 14

.

Тогда амплитуда суммарного колебания ,

где – интенсивность волны от одного источника в точке наблюденияР, где складываются колебания.

При .

Координаты минимумов определяются из условия: , гдеk – номер минимума, .

При – наблюдают резкие максимумы (см. рис. 14).

Дифракционная решётка

Дифракционной решёткой называется система из одинаковых щелей, расположенных на одинаковом расстоянии в линию. Дифракционная решетка являет­ся одним из важнейших спектральных приборов, которому наука обя­зана многими фундаментальными открытиями. Спектр — это по суще­ству код, который будучи расшифрован с помощью того или иного ма­тематического аппарата дает возможность получить ценнейшую информацию о свойствах атомов и внутриатомных процессов.

Рассмотрим простейшую идеализированную решетку, состо­ящую из одинаковых равноотстоящих щелей в непрозрачном экране (см. рис. 15). Пусть ширина каждой щели равна b, а период решет­ки — d = a + b . В решетке реализуется многолучевая интерференция когерентных дифрагированных пучков света, исходящих из ще­лей решетки при ее освещении.

	б)
Рисунок 15

Так как на щелях дифракционной решётки происходит дифракция Фраунгофера, то распределение интенсивности .

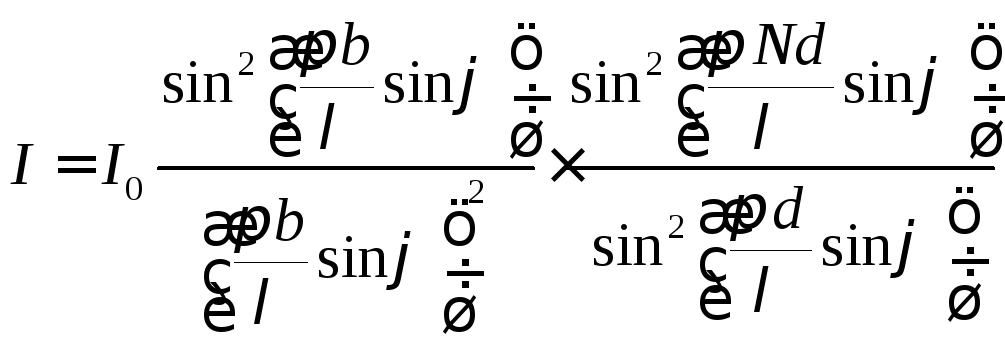
Доказательство: Интенсивность от одной щели

Интенсивность многолучевой интерференции

где – интенсивность волны от одного источника в точке наблюденияР

Полученный результат графически представлен на рис. 16 как зависимость интенсивности дифракционной карти­ны от угла дифракции . Как видим, интерферен­ция многих пучков привела к резкому перераспределению интен­сивности света, обусловленному дифракцией от каждой щели.

Первая дробь в последнем выражении представляет собой плав­ную функцию от (она показана красной линией пунктиром на рис. 16 и отражает дифракционное распределение интенсивности от каж­дой щели).

	Из анализа предыдущей формулы получаем, что дифракционные минимумы будут возникать, когда числитель второй дроби равен нулю, а знаменатель – нет, т.е. когда: , () Если же знаменатель второй дроби равен нулю и , то вторая дробь, как показывает математи­ческий анализ, достигает максимального значения ().
Рисунок 16

Следовательно, под данными углами будут наблюдаться наиболее важ­ные главные макси­мумы, которые являются наиболее интенсивными.

Для главных дифракционных максимумов имеем условие:

Угловая ширина центрального максимума:

.

Основные характеристики спектрального прибора: решетка в каждом порядке разложит падающий на нее свет в спектр. Причем наибольшее отклонение в каждом порядке ис­пытывает красная часть спектра (более длинноволновая).

Основными характеристиками любого спектрального прибо­ра являются угловая дисперсия, разрешающая способность и область дисперсии.

Угловая дисперсия – величина , где– разность углов, соответствующих разным длинами волн,– разность этих длин волн.

Дифференцируя условие максимума получаем

При малых .

Разрешающая сила или разрешающая способность – величина .

	Критерий Релея: Два близких максимума воспринимаются раздельно, если середина одного максимума совпадает с краем другого(см. рис.17). Имеем: - максимума для волны – условие соседнего минимума для волны .
Рисунок 17

По критерию

.

Это и есть искомая формула для разрешающей способности дифракционной решетки. Данная формула дает верхний пре­дел разрешающей способности. Она справедлива при выполне­нии следующих условий:

1. Интенсивность обоих максимумов должна быть одинако­вой.

2. Расширение линий должно быть обусловлено только диф­ракцией.

3. Необходимо, чтобы падающий на решетку свет имел ши­рину когерентности, превышающую размер решетки. То­лько в этом случае все N штрихов решетки будут “рабо­тать” согласованно (когерентно), и мы достигнем желае­мого результата.

Область дисперсии Δλ — это ширина спектрального ин­тервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный аппарат становится непригодным для исследова­ния соответствующего участка спектра.

Длинноволновый конец спектра m-го порядка совпадает с коротковолновым концом спектра (m + 1)-го порядка, если

Значит, область дисперсии Δλ обратно пропорциональна по­рядку спектра m. При работе со спектрами низких порядков (обычно второго или третьего) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал. В этом главное преимущество дифрак­ционных решеток перед интерференционными спектральными приборами, у область дисперсии очень мала.

Дифракция рентгеновских лучей. Для рентгеновского излу­чения кристаллы представляют естественные диф­ракционные решетки.

Дифракцию рентгеновского излу­чения в кристалле можно рассматривать как результат зеркаль­ного отражения от системы параллельных кристаллических плос­костей, т. е. плоскостей, в которых лежат узлы кристаллической решетки. Вторичные волны, отразившись от разных атомных плоскостей, когерентны и будут интерферировать между собой. Показатель преломления всех веществ для рентгеновских лучей близок к единице,

Рисунок 18

поэтому разность хода двух волн, отразивших­ся зеркально от соседних кристаллических плоскостей, равна, как видно из рис. 18, ABC = 2d sin α, где d — межплоскостное расстояние, α — угол скольжения. При этом направления, в ко­торых возникают фраунгоферовы дифракционные максимумы, определяются формулой Брэгга-Вульфа:

Формула Брэгга-Вульфа: – условие максимума при дифракции отражённых рентгеновских лучей на кристалле.

Дифракция рентгеновских лучей от кристаллов получила развитие в двух направлениях: рентгеновская спектроскопия (исследование спектрального состава этого излучения) и рентгеноструктурный анализ (изучение структуры кристаллов).