- •Теорема Гаусса.
- •Поток вектора через поверхность.
- •Поток вектора через замкнутую поверхность.
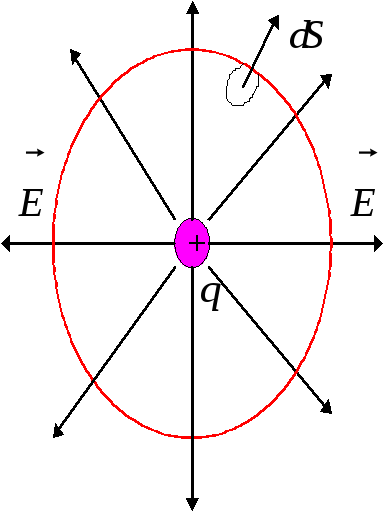
- •Поток вектора сквозь замкнутую поверхность равен с точностью до множителя алгебраической сумме зарядов внутри этой поверхности.
- •Применение теоремы Гаусса для расчета полей.
- •Дифференциальная форма теоремы Гаусса.
-
Какими свойствами обладают электрические заряды? Какой закон описывает взаимодействие неподвижных электрических зарядов? Сформулируйте этот закон. Ответ поясните рисунком.
-
Сформулируйте принцип суперпозиции электростатических полей.
-
Как называется силовая характеристика электрического поля? В каких единицах она измеряется? Дайте определение силовых линий электростатического поля. Когда силовая линия электростатического поля может совпадать с траекторией свободного заряда, помещенного в это поле?
-
Дайте определение однородного электростатического поля. Изобразите это поле графически. В каких устройствах его можно реализовать. Как называются эти устройства.
-
Изобразите на рисунке силовые линии электростатического поля в плоском, цилиндрическом, сферическом конденсаторе, созданного двумя точечными разноименными одноименными зарядами.
-
Сформ
Теорема Гаусса.
Поток вектора через поверхность.
|
|
Рассмотрим
маленькую площадку
в пределах которой вектор напряженности электрического поля имеет постоянное значение:
Для замкнутых поверхностей принято выбирать внешнюю нормаль, |
|
Рисунок 18..6. |
т.е.
нормаль
![]() ,
направленную наружу охватываемой
поверхностью области.
,
направленную наружу охватываемой
поверхностью области.
В
этом случае элементарный
поток
![]() вектора
вектора
![]() через площадку
через площадку
![]() определяется как скалярное произведение
вектора поля на вектор элементарной
площадки:
определяется как скалярное произведение
вектора поля на вектор элементарной
площадки:
|
|
(18.9) |
Т.о., поток вектора есть скалярная величина.
Поток
![]() вектора
вектора
![]() через конечную поверхность
через конечную поверхность
![]() равен:
равен:
|
|
(18.10) |
Поток вектора через замкнутую поверхность.
|
Рисунок 18.7. |
Рассмотрим для начала точечный заряд, окруженный сферической поверхностью с центром, совпадающим с точечным зарядом.
Т.к.
для любого элемента рассматриваемой
поверхности
|
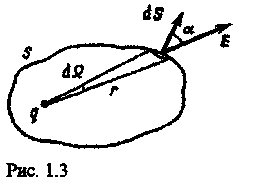
Для
элемента
![]() произвольной замкнутой поверхности
произвольной замкнутой поверхности
![]()
|
|
(18.11) |
где
![]() – телесный угол. Этот угол может принимать
как
– телесный угол. Этот угол может принимать
как
|
|
положительные,
так и отрицательные значения в
зависимости от направления нормали
(значения угла
|
|
Рисунок 18.8 |
Тогда
полный поток вектора
![]() через произвольную замкнутую поверхность
равен
через произвольную замкнутую поверхность
равен
|
|
(18.12) |

![]() ,
ни от выбора самой поверхности.
,
ни от выбора самой поверхности.
|
|
Теперь
пусть поле создается любой системой
зарядов. Тогда всю систему можно
разбить на точечные заряды
|
|
Рисунок 18.9. |
![]() может
быть обобщено для любой системы зарядов,
расположенных произвольным образом,
причем стоящий в правой части уравнения
заряд
может
быть обобщено для любой системы зарядов,
расположенных произвольным образом,
причем стоящий в правой части уравнения
заряд
![]() будет складываться только из зарядов,
находящихся внутри рассматриваемой
замкнутой поверхности
будет складываться только из зарядов,
находящихся внутри рассматриваемой
замкнутой поверхности
![]() .
.
Т.о., получаем:
|
|
(18.13) |
т.е.
из
геометрического правила сложения
векторов
![]() следует, что их потоки
следует, что их потоки
![]() ,
как и заряды
,
как и заряды
![]() ,
складываются алгебраически.
,
складываются алгебраически.
Итак, электростатическая теорема Гаусса:
|
|
(18.14) |
где
![]() суммарный
заряд внутри поверхности
суммарный
заряд внутри поверхности
![]() .
.
Поток вектора сквозь замкнутую поверхность равен с точностью до множителя алгебраической сумме зарядов внутри этой поверхности.
Для
непрерывного распределения заряда с
объемной плотностью
![]() ,
зависящей от координат, имеем
,
зависящей от координат, имеем
|
|
(18.15) |