Лекция №5

(Буланчук О.Н., каф. физики ПГТУ )

Частица в потенциальной яме.

О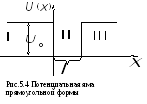пределение: потенциальная яма – область пространства, в котором потенциальная энергия меньше чем в окружающем пространстве (потенциальный барьер наоборот). На Рис.5.4 показана потенциальная яма прямоугольной формы.

Движение частицы в потенциальной яме является удобной моделью для качественного анализа поведения микрочастицы в ограниченном пространстве. Эта модель позволяет выявить почти все основные качественные особенности таких систем.

Рассмотрим задачу о движении частицы в потенциальной яме с бесконечно высокими стенками: . Физически это соответствует ситуации, когда . В этом случае , . Для того, чтобы волновая функция была конечной, в области под знаком экспоненты должен стоять знак плюс, в области минус, тогда при , .

В области

Решение имеет вид , где

На левой границе при :.

Н а правой границе при : . Таким образом получили систему линейных однородных алгебраических уравнений относительно неизвестных коэффициентов:

Из следует , . Далее, воспользовавшись соотношениями

,, получим

.

Константа , поскольку если , то это означает, что частица не существует. Тогда можно удовлетворить, если

.

Значение было отброшено, поскольку это соответствует нулевой волновой функции: отсутствию частицы. Целое число называется квантовым числом, а поскольку оно определяет энергию, то его называют главным квантовым числом. Из следует, что : импульс частицы в потенциальной яме является квантованным. Волновая функция частицы в потенциальной яме имеет вид:

Введем обозначение . Без потери общности, далее коэффициент можно полагать действительным, поскольку исходное уравнение не содержит мнимых величин:

Найдем из условия нормировки

В данном случае называются собственными волновыми функциями оператора кинетической энергии .

Подытожим полученные результаты для частицы в потенциальной яме:

1. Квантово механическое состояние объекта определяется квантовыми числами, которые задают вид волновой функции и определяют значения ряда физических величин (в данном случае квантовое число 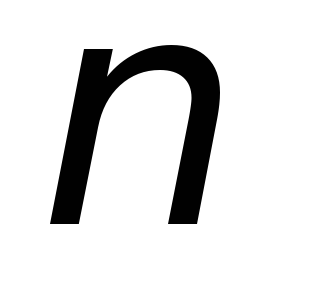определяет энергию и импульс).

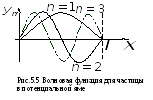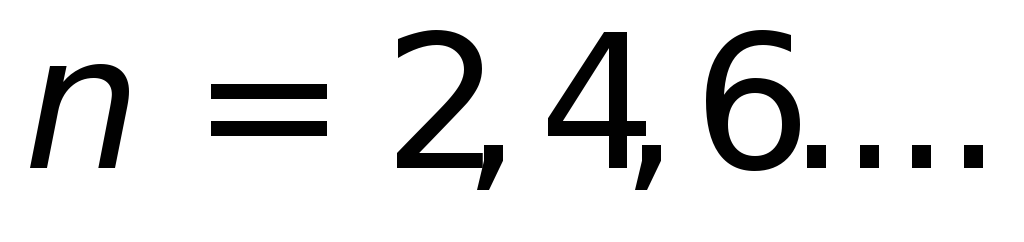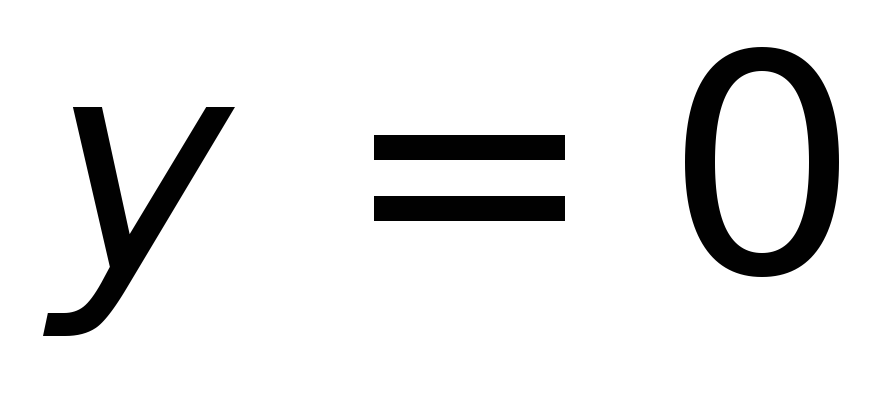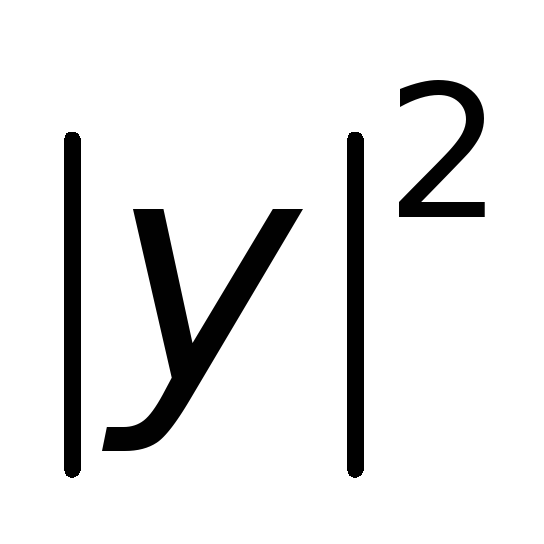2. При частица не может быть обнаружена в середине ямы , а одинаково часто бывает как справа так и слева. Такая ситуация не совместима с классическими представлениями (все положения равновероятны). При число максимумов увеличивается и частицу с одинаковой вероятностью можно обнаружить в любой части потенциальной ямы, что соответствует классическому случаю.

3. Энергетический спектр локализованного объекта оказывается дискретным (квантованным).

Состояние с наименьшим значением энергии называется основным (невозбужденным) состоянием.

4. Для частицы в потенциальной яме существует минимальное значение энергии (полной и кинетической) 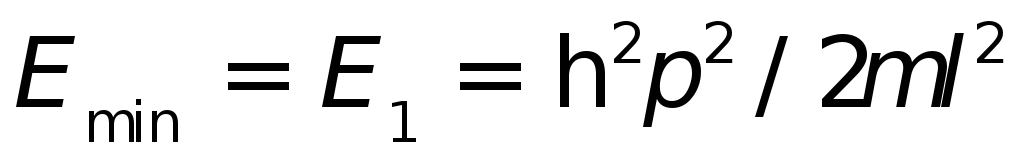(эту энергию часто называют нулевой энергией, хотя она не равна нулю). Таким образом, материальная частица, которая находится в ограниченном пространстве, не может пребывать в состоянии покоя. Почему же мы тогда наблюдаем покоящиеся тела? Для ответа на этот вопрос оценим нулевую энергию для макрочастицы (пылинки массой кг), которая находится в сантиметровой коробочке (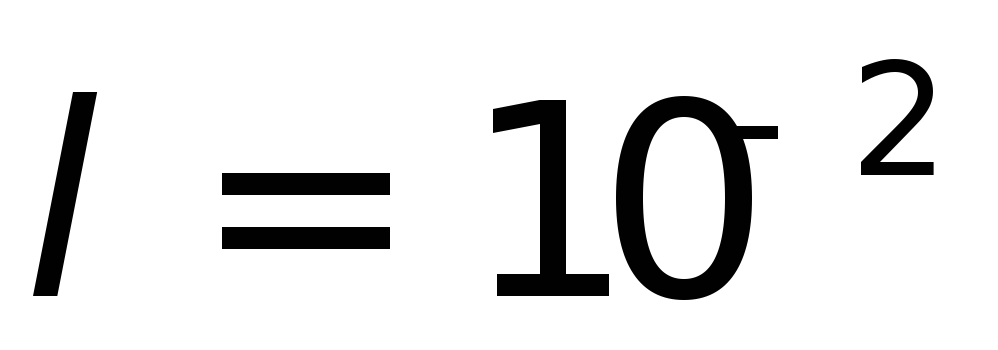м):

Дж=эВ

м/с

Видно, что скорость движения в этом случае ничтожно мала и пылинка практически покоится.

Для электрона в атоме скорость оказывается достаточно большой:

кг, м

ДжэВ

м/с

5. Микрочастица может перейти с одного энергетического уровня на другой, если энергия сообщаемая объекту 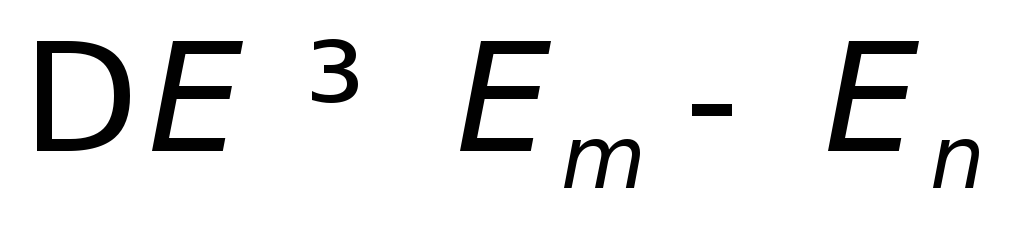. В противном случае она остается невосприимчивой к внешним воздействиям. Покажем, что для макрочастиц эффект квантования энергии оказывается практически незаметным.

Расстояние между энергетическими уровнями будет равно

Из видно, что с увеличением квантового числа разность энергий возрастает. Почему ж при больших энергиях не обнаруживается квантование энергии? Дело в том, что хотя растет, однако относительное изменение энергии при этом будет убывать по закону , т.е., стремится к нулю при увеличении квантового числа. Это означает, что при больших квантовых числах энергия частицы будет изменятся непрерывно.

Оценим для пылинки массой г в потенциальной яме ширины см. Для

ДжэВ

Для электрона в атоме:

ДжэВ.

Из оценок , следует, что энергия макрочастиц будет изменяться практически непрерывным образом, а дискретность будет заметна только для частиц с очень маленькой массой.

Для дискретных энергетических спектров вводится понятие плотности энергетических состояний—число энергетических уровней приходящихся на единичный интервал энергий:

Плотность энергетических состояний обратно пропорциональна расстоянию между энергетическими уровнями. С увеличением уменьшается ( увеличивается).

Замечание 1: Интересна задача о прохождения частицы над потенциальной ямой. В этом случае существует ненулевая вероятность отражения частицы от потенциальной ямы, однако при определенных значениях глубины ямы возможно прохождение частиц без отражения.

Замечание 2: в результате последних экспериментальных исследований было показано, что эффект квантования энергии наблюдается для нейтронов в гравитационном поле Земли (квантование гравитационного поля). В экспериментальной установке наблюдалась повышенная концентрация нейтронов только на определённых дискретных высотах.

3