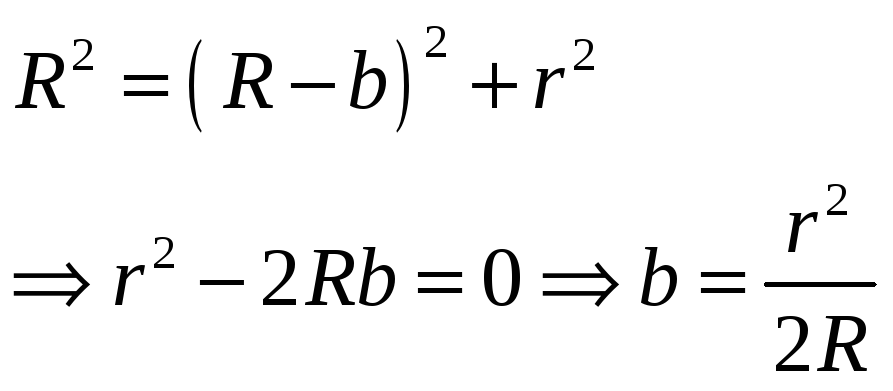физика / interferentsia

Оптика

Одним из следствий системы уравнений Максвелла является уравнение электромагнитной волны:

или .

Анализируя это уравнение, приходим к выводу, что скорость распространения электромагнитных волн , где .

Совпадение значений постоянной и скорости света в вакууме позволило предположить, что свет является электромагнитной волной. Это предположение в дальнейшем получило опытные подтверждения. Поэтому, все действия света характеризуются вектором напряжённости электрического поля.

В прозрачных средах, которые являются или пара- или диамагнетиками, справедливо . Следовательно,. Как известно, относительная электрическая проницаемость диэлектриков может значительно превышать единицу (например, для химически чистой воды). Поэтому скорость распространения света в веществе отличается от скорости света в вакууме. Величина, характеризующая замедление распространения света в веществе, т.е. показывает во сколько раз , называется показателем преломления среды

.

Т.к.  зависит от частоты колебаний, то или .

Следует отметить, что многие задачи оптики, - раздела физики, в котором изучаются оптическое излучение (свет), его распространение и явления, наблюдаемые при взаимодействии света и вещества, могут быть решены с помощью уравнений Максвелла. Однако такие решения сопряжены с достаточно серьезными трудностями. Более простые решения многих из этих вопросов дает волновая оптика, которая изучает характер распространения световых волн в пространстве и времени. Волновая оптика оперирует многими понятиями, свойственными многим волновым процессам.

Большинство волновых процессов можно описать с помощью плоских волн, колебания в которых протекают по гармоническим законам

Величина , определяющая значение напряженностей полей, называется фазой волны.

Волновая поверхность – геометрическое место точек, в которых волна имеет одинаковую фазу. Волновым фронтом называется волновая поверхность с нулевой фазой волны.

Длина волны есть расстояние, на которое перемещается фронт волны за время равное периоду колебаний; в среде , где – длина волны в вакууме и - частота.

Модуль среднего по времени значения плотности потока энергии, переносимой волной, называется интенсивностью волны:

.

Т.к. одним из следствий уравнений Максвелла есть равенство , то .

Пусть имеется монохроматическая волна .

Тогда

.

Свет излучается цугами. Каждый цуг длится порядка с. Поэтому описание волновых процессов с помощью гармонических функций носит ограниченный характер.

В однородной среде свет распространяется прямолинейно (при отсутствии неоднородностей, например, маленьких отверстий). При пересечении световых лучей они не возмущают друг друга (при не слишком больших интенсивностях).

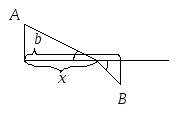
	Отражённый луч лежит в одной плоскости с падающим и с перпендикуляром, восстановленным в точке падения, причём угол падения равен углу отражения. Закон преломления: , где - угол падения, – угол преломления, – скорость в i-й среде, – преломление i-й среды (см. рис. 1).
Рисунок 1.

По определению скорость

.

Таким образом, время, за которое свет преодолеет расстояние от точки 1 до точки 2, а следовательно и фаза волны могут быть выражены через скорость света в вакууме и оптическую длину пути

.

Принцип Ферма: Свет распространяется по такому пути, оптическая длина которого минимальна.

Применим этот принцип для доказательства закона преломления. Для рисунка 1 имеем

.

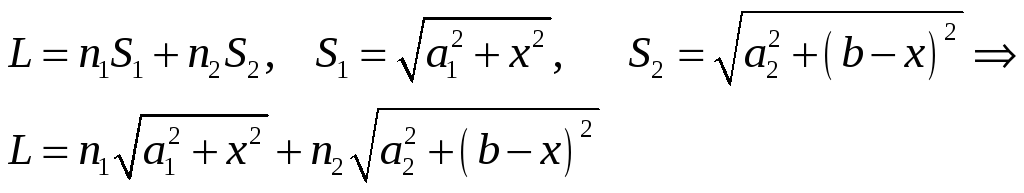
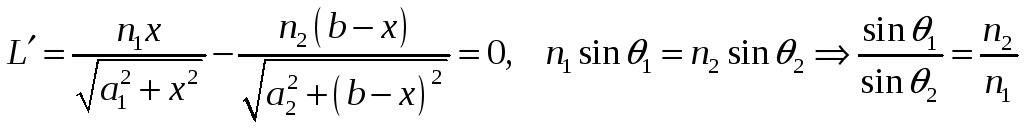Интерференция световых волн

Пусть в какую-то точку приходят две волны с колебаниями одного направления:

, .

Тогда амплитуда результирующего колебания (см. рис. 2)

.

Усреднив по времени, получим для стохастически изменяющихся начальных фаз волн:

(где ), следовательно, . Если разность фаз  остаётся постоянной по времени, то такие лучи называются когерентными. Тогда .
	Рисунок 2.

Таким образом, при постоянстве разности фаз волн будет наблюдаться перераспределения интенсивности.

Явление перераспределения интенсивности называется интерференцией (от лат. inter – взаимно, между собой; ferio – ударяю, поражаю).

Пусть один луч расщепили на два и пустили их по путям и . Тогда у начального луча фаза , у расщеплённых – .

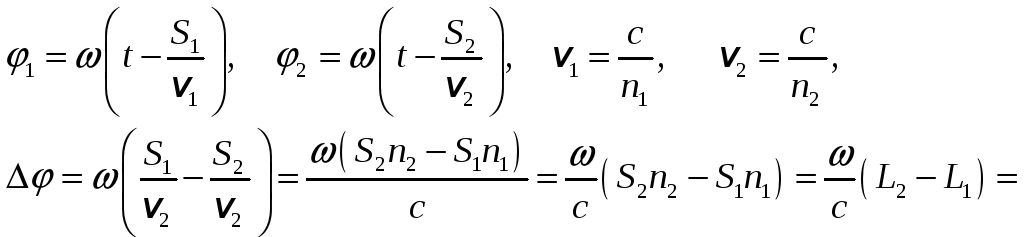
где - волновое число.

Когда оптическая разность хода , будет максимум распределения интенсивности, а когда , будет минимум распределения интенсивности.

Интерференция от двух источников

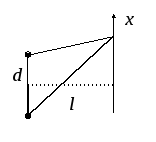
	Рассмотрим интерференцию двух световых волн с постоянными начальными фазами, созданными источниками и , на экране х (см. рис. 3). Расстояние между источниками и экраном равно
Рисунок 3.

– разность хода. При этом

.

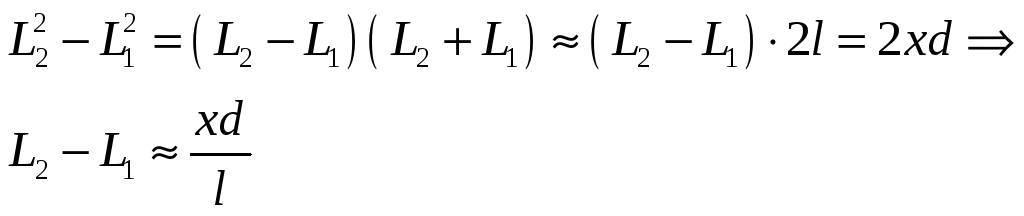Получим координаты положения максимумов и минимумов интенсивности на экране. Оптическая разность хода ,

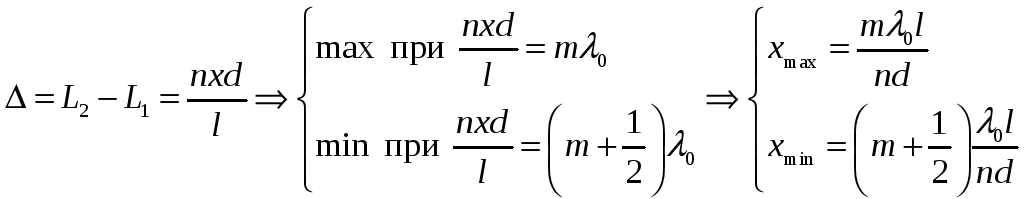где m – любое целое число.

Отсюда видно, что ширина интерференционной полосы

..

Полезно иметь в виду, что размер интерференцион­ной картины обычно не превышает 1 мм, это при расстоянии от источников до экрана порядка нескольких десятков сантимет­ров.

Интерференция на тонких пластинах

	Оптический путь левого луча внутри пластинки: . Оптический путь правого луча, проходимый им в то время, пока второй луч идёт внутри пластинки: Оптическая разность хода
Рисунок 4.

Т.к., то .

При отражении от границы раздела двух сред, если вторая среда более оптически плотная, то происходит скачок фазы на  (в противном случае скачка фаз нет).

Следовательно, . Одним из случаев такой интерференции являются кольца Ньютона.
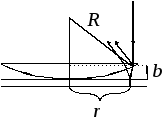
	Это явление наблюдают близи точки соприкосновения плосковыпуклой линзы с плоской стеклянной пластиной. Найдём вначале толщину воздушного зазора между стеклом
Рисунок 5.

Следовательно, оптическая разность хода . (Вспомним, что при отражении от оптически более плотной среды происходит скачок фазы на , чему соответствует оптическая длина ) Если , то кольцо светлое. Если , то кольцо тёмное.

Радиус m-го светлого кольца в отраженном свете: .

Временная когерентность

Когерентность – согласованное протекание колебаний или волновых процессов.

Если частоты колебаний равны и разность их фаз δ постоянна во времени, то такие коле­бания (и волны) называют когерентными. В случае суперпозиции когерентных волн интенсивность результирующего колеба­ния, согласно (1),

(3)

Последнее слагаемое в этой формуле называют интер­ференционным членом.

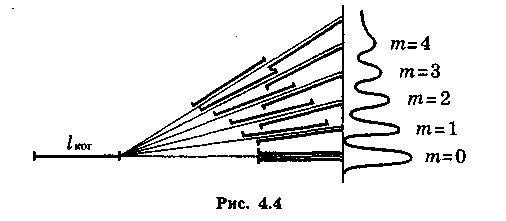
	Длина когерентности. Интерференционная картина по мере удаления от ее середины размывается: неско­лько полос видны, но далее постепенно они исчезают, - степень когерентности складываемых в этих точках экрана колебаний (волн) постепенно
Рисунок 5.

уменьшается, и колебания становятся наконец полностью некогерентными.

Если на рис. 5 когерентные области волн обозначить отрезками, то можно заметить, что при удалении от центра интерференционной картины перекрытие этих областей уменьшается, а затем исчезает.

Исчезновение полос с > 4 означает, что колебания, пришедшие в соответствующие точки экрана от обеих волн, оказываются уже некогерентными между собой.

Данные интервалы обладают длиной когерентно­сти . В рассмотренном случае .

Итак, можно утверждать, что для получения интерфе­ренционной картины необходимо, чтобы оптическая разность хода складываемых колебаний была меньше длины когерент­ности:

Это требование касается всех установок, с помощью которых наблюдают картину интерференции.

В заключение заметим, что длина когерентности связана с так называемым временем когерентности — промежутком времени, в течение которого случайные изменения фазы свето­вой волны в данной точке достигают значения порядка π. За это время волна распространяется на расстояние порядка .

Пространственная когерентность

Пусть в пространстве распространяется сферическая волна. Выясним, какое максимальное расстояние d между двумя точками на её фронте можно взять, при котором волна всё ещё будет когерентна сама себе. Для этого можно обернуть картину и представить, что свет, излученный двумя точечными источниками, находящимися на расстоянии d попадает в точку с координатой u. Тогда оптическая разность хода и если , то волны будут когерентны.

Рисунок 6

– ширина когерентности – предельное расстояние на фронте волны, в двух точках которого волны ещё когерентны. Угол когерентности .