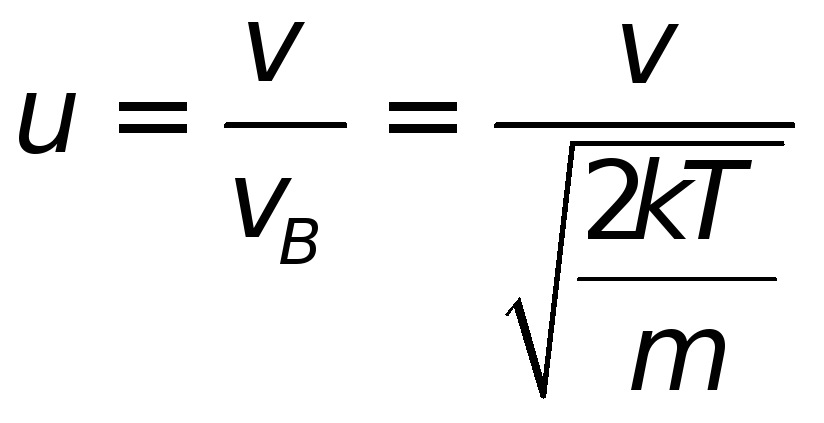- •Лекция 14. Элементы статистической физики.
- •13. 1. Основные понятия.
- •13. 2. Распределение Максвелла (по скоростям).
- •13. 2. 1. Распределение Максвелла (по скоростям) при одномерном движении частиц.
- •13. 2. 2. Распределение Максвелла (по скоростям). Трехмерный случай.
- •13. 2. 3. Средняя, среднеквадратичная и наиболее вероятная скорости частиц.
- •13. 2. 4. Распределение Максвелла в безразмерном виде.
- •13. 2. 5. Распределение Максвелла по энергиям.
- •13. 3. Распределение Больцмана. Газ в силовом поле.
- •13. 3. 1. Барометрическая формула.
13. 2. 3. Средняя, среднеквадратичная и наиболее вероятная скорости частиц.
Наиболее вероятная скорость.
Наиболее вероятная
скорость молекул идеального газа
соответсвует максимуму функции f(v).
Следовательно, эта скорость может быть
найдена из выражения
![]()
|
|
(13.18) |
Средняя скорость молекул.
По определению:
|
|
|
Есть табличный интеграл:
|
|
|
В нашем случае
![]()
Откуда получаем:
|
|
(13.19) |
средняя квадратичная скорость <Vкв> молекул.
|
|
|
По определению![]()
|
|
|
Есть табличный интеграл:
|
|
|
В нашем случае
![]()
![]()
Получаем:
|
|
(13.20) |
Скорости, характеризующие состояние газа.
|
Наиболее вероятная скорость |
|
|
Средняя |
|
|
средняя квадратичная скорость |
|
Где: k – постоянная Больцмана;
m0 – масса молекулы;
Т – термодинамическая температура;
R - молярная газовая постоянная;
![]() - молярная масса.
- молярная масса.
13. 2. 4. Распределение Максвелла в безразмерном виде.
Зачатую бывает удобно провести анализ или решение задачи воспользовавшись распределением Максвелла по скоростям в безразмерном виде. Что получить распределение в такой записи перейдем к безразмерной скорости
|
|
|
Тогда выражение (13.16) примет вид
|
|
(13.21) |
13. 2. 5. Распределение Максвелла по энергиям.
Преобразует
выражение (13.6) с помощью замен
![]() (среднее значение энергии, приходящееся
на одну степень свободы) и
(среднее значение энергии, приходящееся
на одну степень свободы) и![]() (кинетическая энергия частицы). Тогда
(кинетическая энергия частицы). Тогда![]() и
и
|
|
|
или после перехода
к безразмерной величине
![]()
|
|
(13.22) |
Это и есть распределение Максвелла по энергиям
13. 3. Распределение Больцмана. Газ в силовом поле.
|
Перейдем к
рассмотрению газа во внешнем силовом
поле. Для простоты будем полагать, что
в любом физически малом объеме
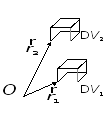
температура газа одинакова. Выделим
в газе два равных по величине объема
|
|
|
Рисунок 13.3. |
Пусть в первом
объеме молекулы газа обладают потенциальной
энергией
![]() ,
а во втором
,
а во втором![]() .
Согласно формулам (13.3) и (13.9) вероятности
того, что молекулы обладают такими
значениями потенциальной энергии (т.е.
.
Согласно формулам (13.3) и (13.9) вероятности
того, что молекулы обладают такими
значениями потенциальной энергии (т.е.![]() ,
и
,
и![]() .)
будут соответственно равны
.)
будут соответственно равны
|
|
(13.23) |
Здесь
![]() - некоторый числовой множитель.
- некоторый числовой множитель.
С другой стороны
эти вероятности
![]() и
и![]() должны относиться друг к другу в той же
пропорции, что и количества частиц в
выбранных объемах при одинаковых в них
температурах
должны относиться друг к другу в той же
пропорции, что и количества частиц в
выбранных объемах при одинаковых в них
температурах
|
|
(13.24) |
Подставим в левую
часть этого равенства (13.23), а числитель
и знаменатель правой дроби поделим на
величину выбранного объема
![]() .
Тогда учтя, что концентрация частиц
.
Тогда учтя, что концентрация частиц![]() ,
после упрощений получаем
,
после упрощений получаем
|
|
|
Отсюда следует, что
|
|
(13.25) |
или
|
|
(13.26) |
где
![]() - концентрация частиц в местоположении
частиц газа с нулевой потенциальной
энергией. Данное выражениеназывается
распределение Больцмана
(при постоянной температуре).
- концентрация частиц в местоположении
частиц газа с нулевой потенциальной
энергией. Данное выражениеназывается
распределение Больцмана
(при постоянной температуре).
Анализ данного выражения показывает, что силовое поле принуждает собираться частицы газа в местах с минимальной потенциальной энергией, а тепловое движение приводит к разбрасыванию частиц по пространству.