
4. Управляющие структуры
.pdf
Лабораторная работа 4
Управляющие структуры
Цели:
1.Получение практических навыков создания программ разветвляющейся структуры.
2.Получение практических навыков создания программ циклической структуры.
Для выполнения лабораторной работы необходимо предварительно изучить теоретический материал, изложенный в разделе «Управляющие структуры» конспекта лекций.
|
|
|
|
|
. |
|
|
Часть 1. |
|
S |
|
|
|
|
|
. |
|
|
Управляющие структуры организации ветвлений в программе |
||||
|
|
. |
V |
|
|
|
|
G |
|
|
|
|
|
Molchanova |
|
|
|
|
|
. |
|
|
|
1. |
Варианты задач выбрать в соотвествииA |
с номером своей фамилии в журнале акаде- |
|||
мической группы. |
Bursa |
|
|
|
|
2. |
Составить и документировать алгоритмы решения задач. |
|
|||
3. |
В соответствии с сосавленными алгоритмами решения задач написать, выполнить и |
||||
документировать консольные программы Программы должны правильно функционировать при любых значениях исходных данных.
4. Корректность работы программ проверить тестированием, применив тесты «белый ящик» и «черный ящик».
5. В программах обязательно использовать операторы: безусловной передачи управления, условной передачи управления, выбора варианта.
Задача 1
1.Написать программу, которая вычисляет частное двух чисел. Программа должна проверять правильность введенных пользователем данных и, если они неверные (делитель равен нулю), выдавать сообщение об ошибке.
Вычисление частного.
Введите в одной строке делимое и делитель,затем нажмите <Enter>.
120
Вы ошиблись. Делитель не должен быть равен нулю.
2.Написать программу вычисления площади кольца. Программа должна проверять правильность исходных данных. Ниже приведен рекомендуемый вид экрана во время выполнения программы:
Вычисление площади кольца. Введите исходные данные:
55

Радиус кольца (см) -> 3.5 Радиус отверстия (см) -> 7
Ошибка! Радиус отверстия не может быть больше радиуса кольца.
3.Написать программу, которая переводит время из минут и секунд в секунды. Программа должна проверять правильность введенных пользователем данных и в случае, если данные неверные, выводить соответствующее сообщение. Рекомендуемый вид экрана во время выполнения программы приведен ниже:
Введите время (минут.секунд) -> 2.90 Ошибка! Количество секунд не может быть больше 60 Для завершения нажмите <Enter>
4.Написать программу, которая проверяет, является ли год високосным.
Введите год, например 2000, и нажмите <Enter> 2001
2000 год - не високосный
Для завершения нажмите <Enter>
|
|
|
|
|
|
|
. |
5. |
Написать программу вычисления сопротивления электрической цепи, состоящей из |
||||||
|
|
|
|
|
|
|
S |
двух сопротивлений. Сопротивления могут быть соединены последовательно или параллель- |
|||||||
но. |
|
|
|
|
|
. |
|
|
|
|
|
|
. |
V |
|
Вычисление сопротивления электрической цепи. |
|
|
|||||
Введите исходные данные: |
|
G |
|
|
|||
х2 = -28.449 |
|
|
|
|
|||
Molchanova |
|
|
|||||
Величина первого сопротивления (Ом) -> 15 |
|
|
|||||
Величина второго сопротивления (Ом)-> 27.3 |
|
|
|||||
|
|
|
A |
|
|
|
|
Тип соединения (1 — последовательное. |
, 2 — параллельное) -> 2 |
||||||
Сопротивление цепи: 9.68 Ом |
|
|
|
|
|
||
|
|
Bursa |
|
|
|
|
|
6. |
Написать программу решения квадратного уравнения. Программа должна прове- |
||||||
рять правильность исходных данных и в случае, если коэффициент при второй степени неизвестного равен нулю, выводить соответствующее сообщение.
Решение квадратного уравнения
Введите в одной строке значения коэффициентов и нажмите <Enter>
12 27 -10
Корни уравнения:
х1 = -25.551
7. Написать программу вычисления стоимости покупки с учетом скидки. Скидка в 10% предоставляется, если сумма покупки больше 1000 руб.
Вычисление стоимости покупки с учетом скидки Введите сумму покупки и нажмите <Enter>
1200
Вам предоставляется скидка 10% Сумма покупки с учетом скидки: 1080.00 руб.
8. Написать программу вычисления стоимости покупки с учетом скидки. Скидка в 3% предоставляется, если сумма покупки больше 500 руб, в 5% — если сумма больше 1000 руб.
Вычисление стоимости покупки с учетом скидки. Введите сумму покупки и нажмите <Enter>
640
Вам предоставляется скидка 3%
56

Сумма с учетом скидки: 620.80 руб.
9. Написать профамму проверки знания даты основания Санкт-Петербурга. В случае неправильного ответа пользователя, программа должна выводить правильный ответ.
В каком году был основан Санкт-Петербург? Введите число и нажмите <Enter>
1705
Вы ошиблись, Санкт-Петербург был основан в 1703 году.
10. Написать программу проверки знания даты начала Второй Мировой войны. В случае неправильного ответа пользователя, программа должна выводить правильный ответ.
В каком году началась Вторая Мировая война? Введите число и нажмите <Enter>
1939
Правильно.
11. Напишите программу проверки знания истории архитектуры. Программа должна
вывести вопрос и три варианта ответа. Пользователь должен выбрать правильный ответ и |
|||||
ввести его номер. |
|
|
|
|
. |
Архитектор Исаакиевского собора: |
|
|
S |
||
|
. |
||||
Доменико Трезини |
|
|
|
||
|
|
. |
V |
|
|
Огюст Монферран |
|
|
|
||
|
|
|
|
|
|
Карл Росси |
|
|
G |
|
|
1 |
|
|
|
|
|
Molchanova |
|
|
|||
Введите номер правильного ответа и нажьлите <Enter> |
|
||||
3 |
|
A |
|
|
|
Вы ошиблись. |
|
. |
|
|
|
Архитектор Исаакиевского собора — Огюст Монферран. |
|
||||
Bursa |
|
|
|
|
|
12. Напишите профамму проверки знания истории архитектуры. Программа должна вывести вопрос и три варианта ответа. Пользователь должен выбрать правильный ответ и ввести его номер.
Невский проспект получил свое название:
По имени реки, на берегах которой расположен Санкт-Петербург По имени близлежащего монастыря Александро-Невской лавры 3. В память о знаменитом полководце Александре Невском Введите номер правильного ответа и нажмите <Enter>
Вы ошиблись. Правильный ответ: 2.
13. Написать программу, которая сравнивает два введенных с клавиатуры числа. Программа должна указать, какое число больше, или, если числа равны, вывести соответствующее сообщение.
Введите в одной строке два целых числа и нажмите <Enter>.
34 67
34 меньше 67
14. Написать программу, которая выводит пример на умножение двух однозначных чисел, запрашивает ответ пользователя, проверяет его и выводит сообщение "Правильно!" или "Вы ошиблись" и правильный результат.
Сколько будет 6x7?
Введите ответ и нажмите <Enter>
57

-> 56
Вы ошиблись. 6x7=42
15. Написать программу, которая выводит пример на вычитание (в пределах 100), запрашивает ответ пользователя, проверяет его и выводит сообщение "Правильно!" или "Вы ошиблись" и правильный результат.
Сколько будет 83-17?
Введите ответ и нажмите <Enter>
->б7
Вы ошиблись. 83-17=66
Задача 2
Таблица 4.1
|
|
|
|
. |
|
|
|
|
S |
|
|
|
. |
|
|
|
. |
V |
|
|
|
G |
|
|
Molchanova |
|
|
||
|
. |
|
|
|
Bursa |
A |
|
|
|
|
|
|
|
|
58
|
|
|
|
. |
|
|
|
|
S |
|
|
|
. |
|
|
|
. |
V |
|
|
|
G |
|
|
Molchanova |
|
|
||
|
. |
|
|
|
Bursa |
A |
|
|
|
|
|
|
|
|
59

Часть 2.
Управляющие структуры организации цилов в программе
1. |
Варианты задач выбрать в соотвествии с номером своей фамилии. в журнале акаде- |
|||||
|
|
|
|
|
. |
|
мической группы. |
|
|
|
|
S |
|
2. |
Составить и документировать алгоритмы решения задач |
|||||
|
|
|
|
. |
|
|
3. |
В соответствии с сосавленными алгоритмами решения задач написать, выполнить и |
|||||
документировать консольные программы Программы должныVправильно функционировать |
||||||
|
|
Molchanova |
|
|||
при любых значениях исходных данных |
. |
|
|
|||
|
|
|
A |
|
|
|
4. |
Корректность работы программ проверитьG |
тестированием, применив тесты «белый |
||||
ящик» и «черный ящик». |
|
|
|
|
|
|
5. |
В программах обязательно использовать операторы организации цилов: с предусло- |
|||||
|
Bursa |
|
|
|
|
|
вием, с постусловием, с параметрами цикла, которые изменяются с заданным шагом.
Для ряда, члены которого вычисляются по формуле, соответствующей Вашему индивидуальному заданию, подсчитать сумму членов ряда с точностью 0.000001 и сумму первых 10 членов ряда. Если Вы считаете это необходимым, можете упростить или преобразовать выражение.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
Вариант 6.
60

Вариант 7. |
|
|
|
Вариант 8. |
|
|
|
Вариант 9. |
|
|
|
Вариант 10. |
|
|
|
Вариант 11. |
|
|
|
Вариант 12. |
|
|
|
Вариант 13. |
|
|
. |
|
|
|
|
Вариант 14. |
|
|
S |
|
|
|
|
|
|
. |
|
Вариант 15. |
. |
V |
|
|
|
||
Общий метод решения |
G |
|
|
|
|
|
|
|
. |
|
|
Очевидно, что процесс подсчета суммы членов ряда должен быть итерационным: сле- |
|||
|
A |
|
|
|
Molchanova |
|
|
дует повторять вычисления по одной и той же формуле при значениях n=0, 1, 2, ... . На каждой итерации цикла Bursaследует выполнять вычисления по заданной формуле для текущего значения n, т.е. подсчитывать очередной член ряда. Полученное значение следует прибавлять к переменной, которая представляет сумму. Эта переменная в каждой итерации будет содержать в себе сумму всех уже обработанных членов ряда, следовательно, ее начальное значение (когда ни один член еще не обработан) должно быть 0. После вычисления суммы при значении n=9 следует вывести значение суммы - это один из результатов программы в соответствии с заданием (берется значение 9, т.к. первый член ряда вычисляется при n=0, таким образом, девятый - при n=9). После вычисления каждого члена ряда (но до прибавления его значения к сумме) следует сравнить полученное значение с заданным пределом точности. Из-за того, что значение члена ряда может быть как положительным, так и отрицательным, при сравнении следует использовать абсолютное значение. Если абсолютное значения члена ряда не превышает предела точности, следует закончить вычисления: выйти из цикла напечатать значение суммы и завершить программу.
Алгоритм вычисления 2n
Для выполнения возведения в степень можно применить библиотечную функцию C pow(x,y) . Но есть возможность получения этого значения более эффективным способом. В каждой следующей итерации цикла значение этого выражения вдвое больше, чем в предыдущей. Так что, будет целесообразно выделить отдельную переменную для сохранения значения 2n. Ее начальное значение должно быть 20 = 1, а в конце каждой итерации оно должно удваиваться.
Алгоритм вычисления (-1)n
В этом случае также нецелесообразно применять функцию возведения в степень. Значение этого выражения будет равно 1 при четных значениях n и -1 - при нечетных. Так что,
61

можно выделить переменную для сохранения значения этого выражения. Ее начальное значение должно быть (-1)0=1, а в конце каждой итерации оно должно менять знак на противоположный.
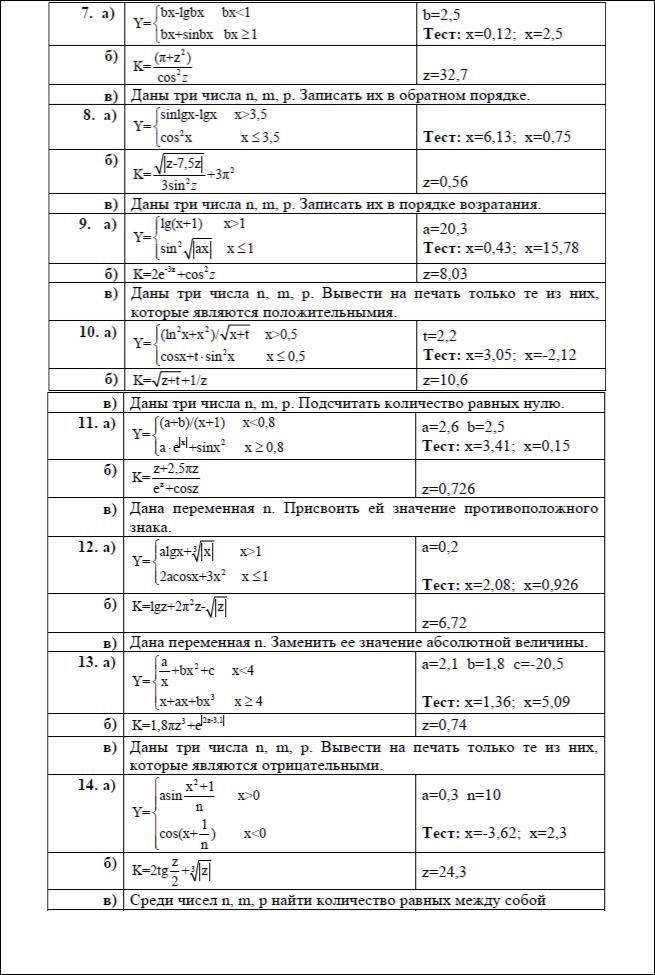
Задача 2.
Для функции Y = f(X), график которой приведен в Вашем индивидуальном задании, вывести на экран значения Y для Х = 0, 0.25, 0.5, ... 19.75. Необязательное для выполнения дополнительное требование – вывести на консольный экран график функции.
Вариант 1.
Вариант 2.
Вариант 3.
Вариант 4.
Вариант 5.
|
|
|
|
. |
|
|
|
|
S |
|
|
|
. |
|
|
|
. |
V |
|
|
|
G |
|
|
Molchanova |
|
|
||
|
. |
|
|
|
Bursa |
A |
|
|
|
|
|
|
|
|
Вариант 6.
Вариант 7.
62
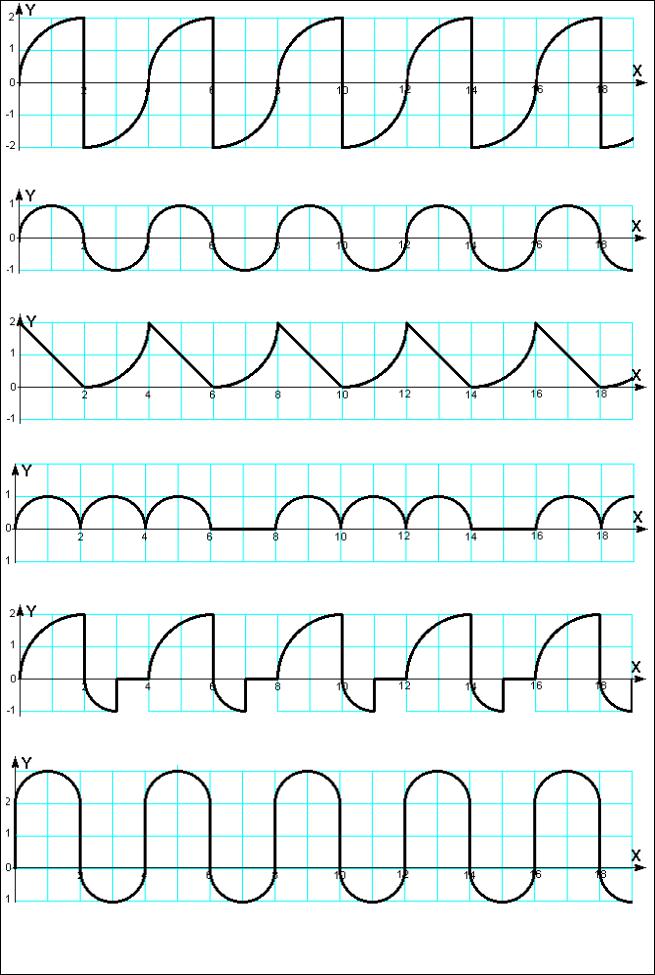
Вариант 8.
Вариант 9.
Вариант 10.
Вариант 11.
Вариант 12.
|
|
|
|
. |
|
|
|
|
S |
|
|
|
. |
|
|
|
. |
V |
|
|
|
G |
|
|
Molchanova |
|
|
||
|
. |
|
|
|
Bursa |
A |
|
|
|
|
|
|
|
|
Вариант 13.
63

Вариант 14.
Вариант 15. |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
. |
|
|
|
|
. |
V |
|
|
|
|
G |
|
|
|
Molchanova |
|
|
||
Пример анализа задачи: |
|
. |
|
|
|
Bursa |
A |
|
|
|
|
Из приведенного в индивидуальном задании графика функции видно, что функция является периодической, с периодом 4. В заданный интервал вкладываются 5 периодов функции. Так что, программа может содержать в себе цикл, в котором 5 раз будут выполняться одни и те же вычисления. В каждой итерации этого цикла должны перебираться значения x от 0 до 3.75 с шагом 0.25, т.е., должен быть вложенный цикл. В каждой итерации вложенного цикла вычисляется значение y для текущего x и выводятся результаты.
Анализ приведенного графика показывает, что каждый период его состоит из трех частей: на отрезке 0<=x<=1 график является прямой, на отрезке 1<=x<=3 - дугой, а на отрезке 3<=x<=4 - другой прямой. Следовательно, во вложенном цикле должно быть разветвление, в котором определяется текущее значение x и обеспечиваются вычисления для первого, второго или третьего случая.
Вычисление функции на отрезке 0 – 1
На этом отрезке функция является функцией прямой. Формула прямой: y=ax+b. Для этого случая a=2, b=-1. Итак, окончательная формула для отрезка 0<=x<=1 такая: y=2x-1
Вычисление функции на отрезке 1 - 3
На этом отрезке функция является частью окружности. Формула окружности: (x- x0)2+(y-y0)2=R2, где (x0, y0) - координаты центра окружности, а R - радиус. Отсюда y можно
определить как:  . В нашем случае R=1, а координаты центра - (2, 1). Извлечение квадратного корня дает два значения - положительное и отрицательное, в нашем случае ис-
. В нашем случае R=1, а координаты центра - (2, 1). Извлечение квадратного корня дает два значения - положительное и отрицательное, в нашем случае ис-
64
