- •Задания для самостоятельной работы
- •Задача №2. Теоремы сложения и умножения вероятностей.
- •Задача №3. Формула полной вероятности. Формулы Бейеса.
- •Задача №4. Предельные теоремы в схеме Бернулли.
- •Задача №5. Дискретные случайные величины.
- •Задача №6 Непрерывные случайные величины.
- •Математическая статистика. Задача №7
- •Задача №8
- •Литература
Задача №6 Непрерывные случайные величины.
Случайная
величина задана интегральной функцией
распределения
![]() .
Определить:
.
Определить:
1) дифференциальную
функцию
![]() ;
;
2) математическое ожидание и дисперсию случайной величины Х;
3). построить
графики
![]() и
и![]() .
.
|
№ |
Интегральная
функция
|
№ |
Интегральная
функция
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
Математическая статистика. Задача №7
В результате эксперимента получены 40 данных, записанных в виде статистического ряда. Требуется:
Записать значения результатов эксперимента в виде вариационного ряда;
Найти размах варьирования и разбить его на 6 интервалов;
Построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
Найти числовые характеристики выборки
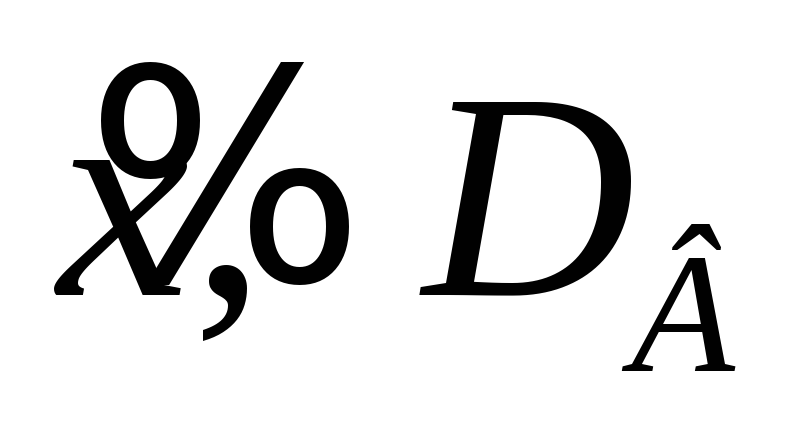 ;
;Приняв в качестве нулевой гипотезу
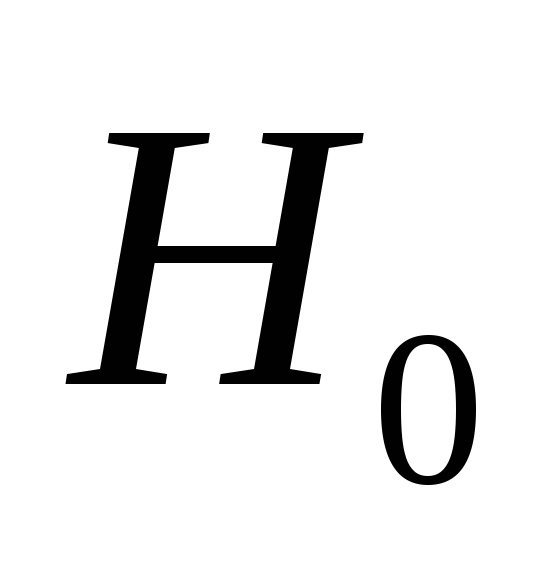 :
генеральная совокупность, из которой
извлечена выборка имеет нормальное
распределение, проверить её, пользуясь
критерием Пирсона при уровне значимости
:
генеральная совокупность, из которой
извлечена выборка имеет нормальное
распределение, проверить её, пользуясь
критерием Пирсона при уровне значимости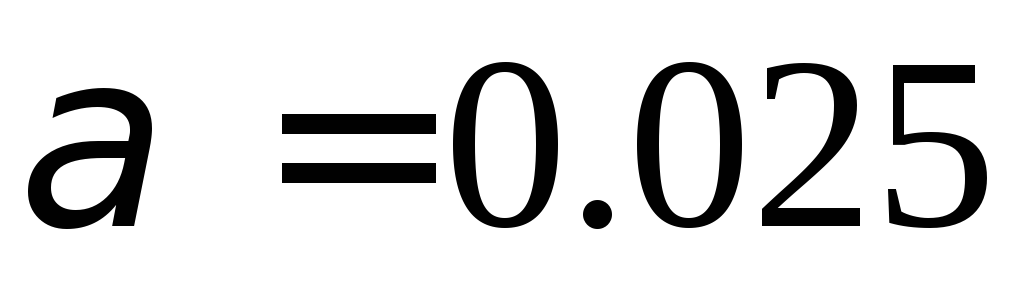 ;
;Найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности
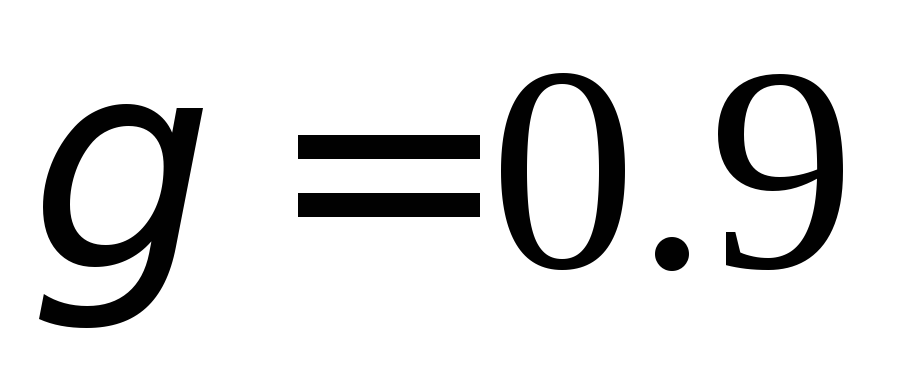 .
.
Указание: Значения элементов выборки расположены в столбцах таблицы 3. Номер столбца, относительно которого необходимо проводить вычисления, совпадает с последней цифрой учебного шифра.
ТАБЛИЦА 3
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
15.9 |
20.1 |
18.3 |
18.6 |
20.1 |
18.2 |
17.3 |
19.0 |
16.9 |
18.2 |
|
2 |
16.8 |
21.2 |
19.5 |
19.3 |
20.4 |
17.8 |
18.0 |
20.3 |
16.7 |
18.2 |
|
3 |
13.2 |
17.6 |
17.3 |
14.5 |
18.4 |
16.1 |
15.8 |
16.5 |
14.5 |
15.8 |
|
4 |
15.5 |
20.1 |
19.1 |
16.7 |
20.9 |
18.6 |
16.9 |
19.4 |
15.3 |
18.0 |
|
5 |
14.6 |
18.8 |
17.8 |
17.1 |
19.6 |
17.5 |
16.3 |
18.3 |
15.8 |
17.4 |
|
6 |
15.6 |
20.0 |
19.1 |
17.2 |
20.5 |
18.7 |
18.0 |
18.6 |
16.5 |
17.9 |
|
7 |
16.9 |
20.7 |
20.1 |
20.3 |
20.4 |
19.6 |
18.5 |
20.8 |
18.2 |
19.3 |
|
8 |
14.1 |
18.4 |
17.3 |
17.7 |
19.1 |
17.9 |
16.9 |
18.1 |
16.4 |
16.8 |
|
9 |
13.6 |
18.3 |
16.6 |
17.3 |
18.7 |
16.6 |
16.0 |
17.4 |
17.0 |
17.4 |
|
10 |
15.2 |
20.2 |
19.4 |
16.2 |
19.8 |
16.8 |
16.2 |
19.3 |
15.2 |
17.5 |
|
11 |
15.0 |
18.6 |
18.7 |
17.4 |
19.5 |
18.8 |
16.7 |
18.7 |
16.7 |
18.4 |
|
12 |
14.9 |
19.0 |
18.5 |
17.7 |
19.5 |
18.8 |
17.2 |
18.7 |
16.7 |
17.8 |
|
13 |
16.6 |
19.0 |
19.6 |
17.9 |
20.3 |
18.8 |
16.5 |
19.2 |
15.5 |
18.4 |
|
14 |
12.7 |
17.4 |
16.8 |
16.5 |
18.1 |
16.2 |
15.1 |
18.3 |
15.4 |
16.5 |
|
15 |
16.1 |
19.3 |
18.7 |
18.2 |
20.9 |
19.8 |
16.8 |
19.0 |
16.6 |
18.9 |
|
16 |
14.2 |
19.0 |
18.4 |
16.9 |
19.2 |
17.4 |
16.3 |
19.4 |
15.5 |
17.1 |
|
17 |
16.6 |
21.1 |
19.7 |
19.7 |
20.8 |
20.1 |
18.5 |
20.5 |
18.5 |
19.4 |
|
18 |
15.1 |
19.2 |
18.2 |
18.0 |
20.2 |
18.9 |
17.0 |
19.0 |
16.6 |
18.2 |
|
19 |
17.0 |
21.9 |
21.8 |
20.0 |
20.9 |
20.9 |
20.2 |
22.6 |
17.9 |
19.2 |
|
20 |
16.9 |
21.4 |
19.2 |
18.2 |
21.1 |
18.6 |
17.8 |
19.3 |
16.4 |
18.1 |
|
21 |
16.7 |
21.1 |
19.3 |
20.0 |
20.4 |
19.3 |
18.8 |
19.7 |
18.7 |
19.1 |
|
22 |
14.3 |
19.1 |
16.6 |
18.4 |
19.0 |
17.9 |
17.1 |
17.1 |
18.8 |
18.1 |
|
23 |
11.3 |
16.6 |
14.9 |
13.7 |
17.8 |
14.6 |
14.6 |
15.2 |
13.9 |
14.5 |
|
24 |
16.0 |
19.1 |
19.9 |
18.1 |
19.2 |
17.2 |
15.9 |
20.3 |
15.4 |
17.9 |
|
25 |
16.8 |
21.4 |
20.8 |
19.4 |
20.4 |
19.0 |
18.9 |
21.1 |
17.6 |
19.0 |
|
26 |
13.6 |
20.1 |
17.9 |
17.6 |
18.6 |
15.7 |
16.9 |
19.9 |
16.2 |
16.4 |
|
27 |
17.6 |
21.5 |
20.8 |
20.5 |
21.2 |
20.4 |
19.5 |
21.0 |
18.3 |
19.9 |
|
28 |
14.6 |
18.2 |
18.6 |
18.5 |
19.2 |
18.8 |
17.2 |
19.4 |
17.0 |
18.5 |
|
29 |
14.2 |
18.8 |
17.2 |
16.6 |
19.6 |
17.4 |
16.8 |
17.8 |
14.9 |
16.4 |
|
30 |
14.4 |
19.0 |
19.1 |
17.6 |
18.4 |
16.7 |
15.4 |
20.6 |
15.7 |
17.2 |
|
31 |
14.7 |
19.6 |
17.9 |
17.0 |
20.1 |
18.4 |
17.4 |
18.3 |
16.2 |
17.3 |
|
32 |
15.4 |
20.3 |
19.1 |
18.0 |
19.3 |
17.8 |
17.8 |
19.3 |
17.1 |
17.7 |
|
33 |
17.6 |
21.9 |
20.8 |
21.0 |
21.0 |
20.2 |
18.7 |
22.6 |
17.8 |
19.4 |
|
34 |
14.5 |
19.7 |
18.8 |
17.3 |
18.8 |
17.0 |
17.2 |
19.0 |
16.7 |
17.3 |
|
35 |
14.2 |
18.3 |
17.6 |
17.2 |
18.9 |
17.0 |
15.4 |
19.0 |
15.1 |
17.0 |
|
36 |
16.6 |
21.6 |
20.5 |
18.8 |
20.8 |
18.7 |
18.4 |
21.2 |
16.9 |
18.6 |
|
37 |
13.3 |
17.8 |
17.5 |
16.6 |
18.1 |
17.3 |
16.3 |
17.6 |
16.6 |
17.0 |
|
38 |
14.7 |
20.0 |
20.2 |
17.7 |
18.8 |
18.0 |
18.4 |
20.1 |
17.7 |
17.9 |
|
39 |
12.9 |
17.0 |
15.1 |
15.5 |
19.1 |
17.1 |
14.7 |
15.9 |
14.9 |
16.4 |
|
40 |
15.3 |
19.6 |
17.5 |
17.4 |
20.7 |
18.6 |
16.5 |
18.6 |
15.3 |
17.5 |

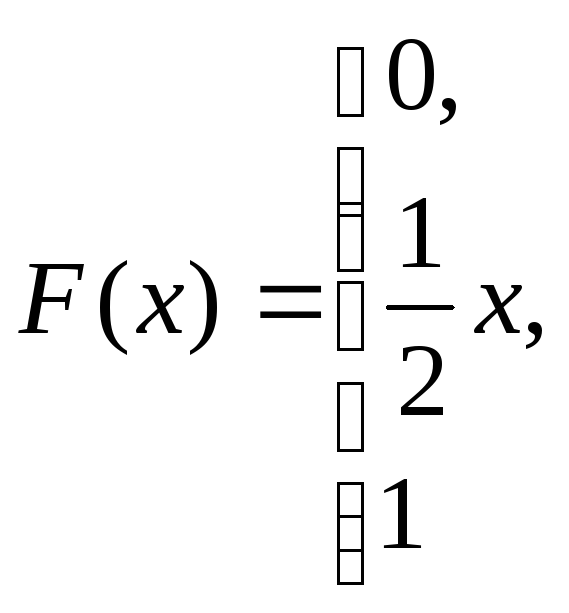 при
при 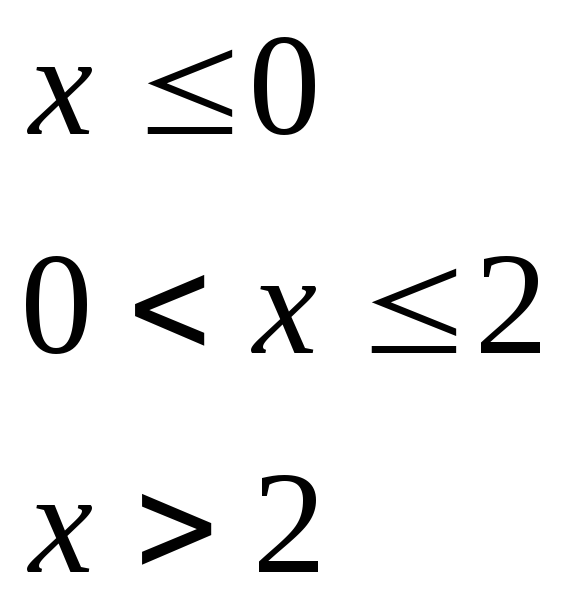
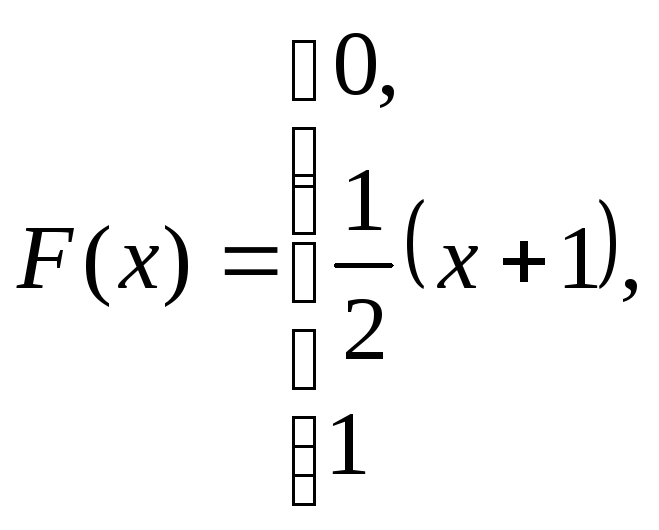 при
при 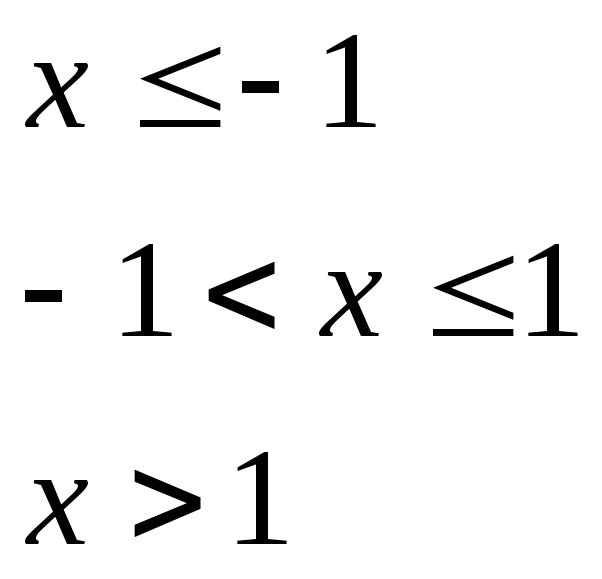
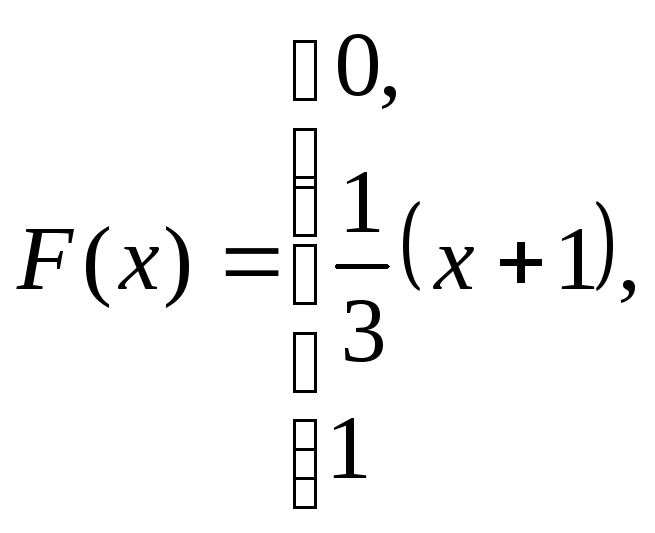 при
при 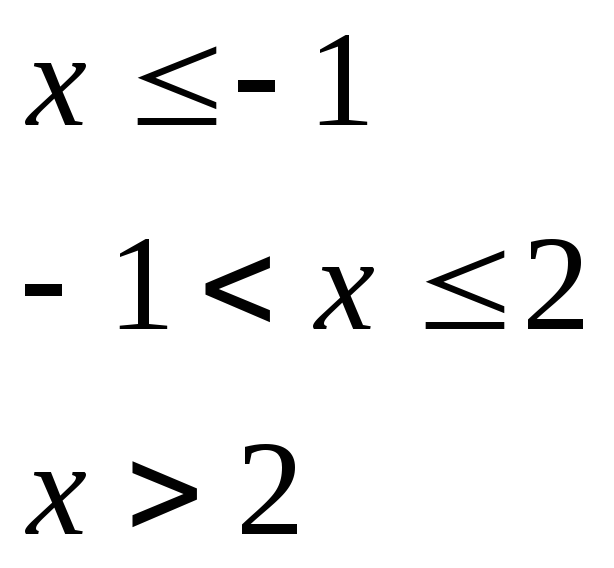
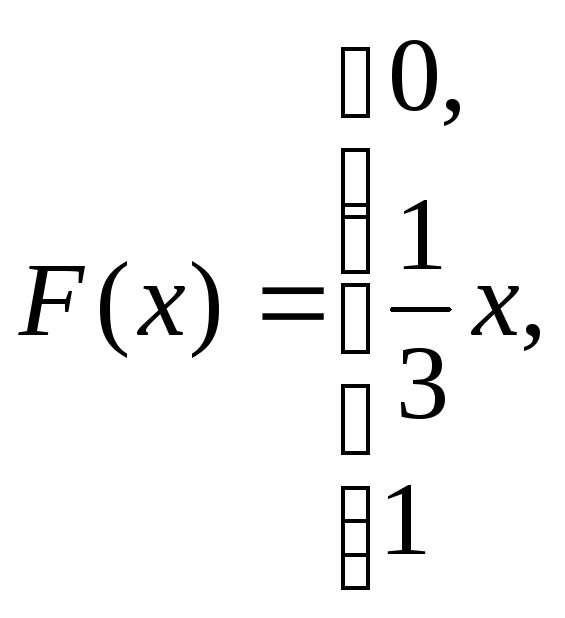 при
при 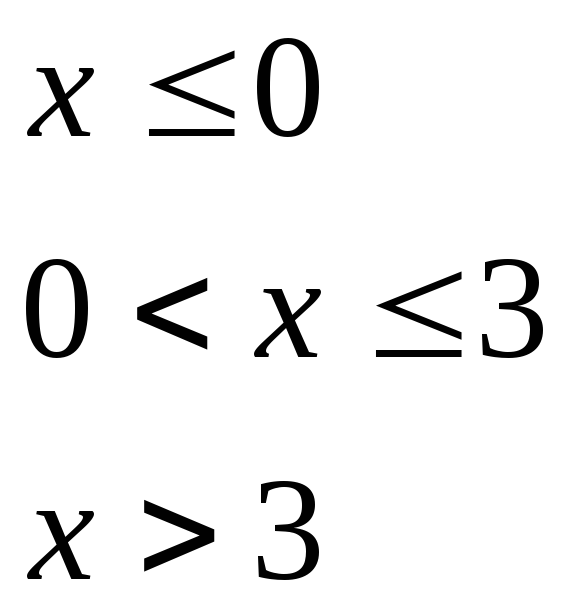
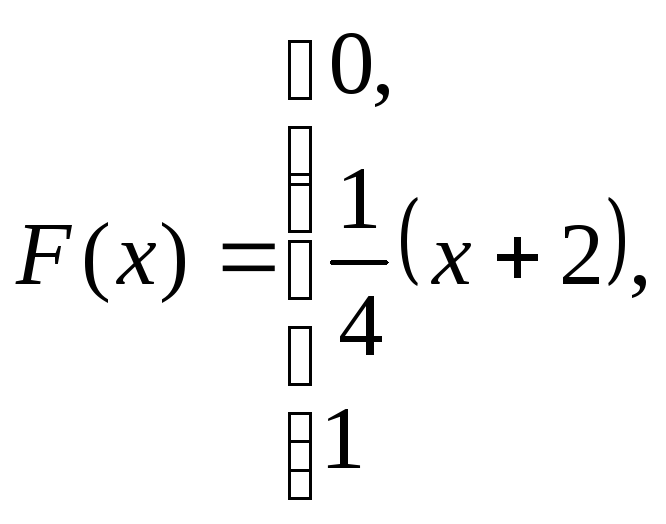 при
при 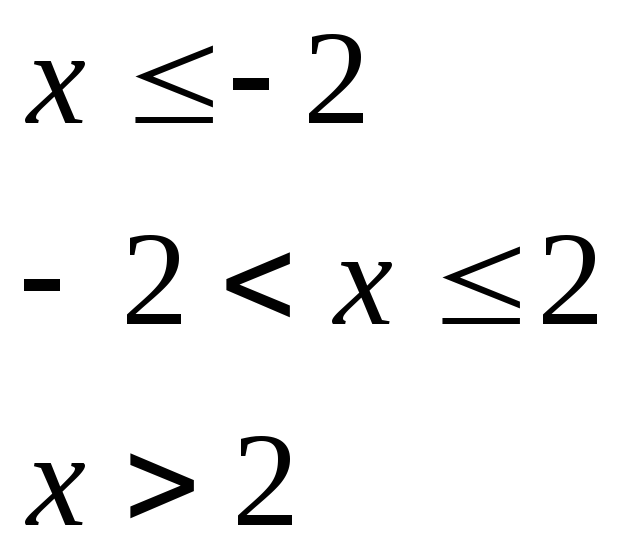
 при
при 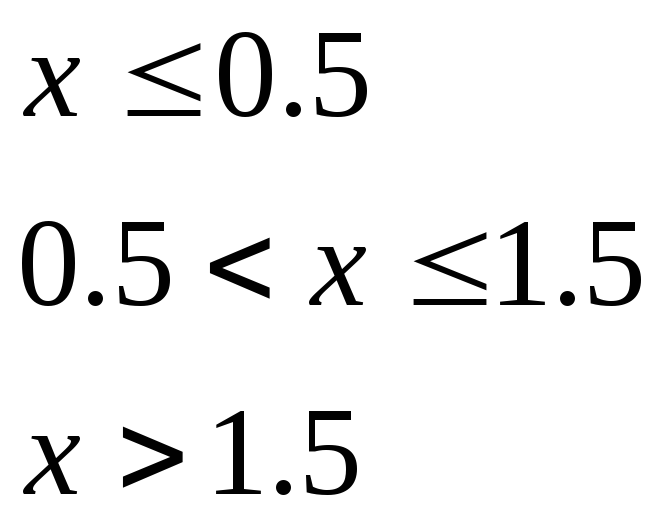
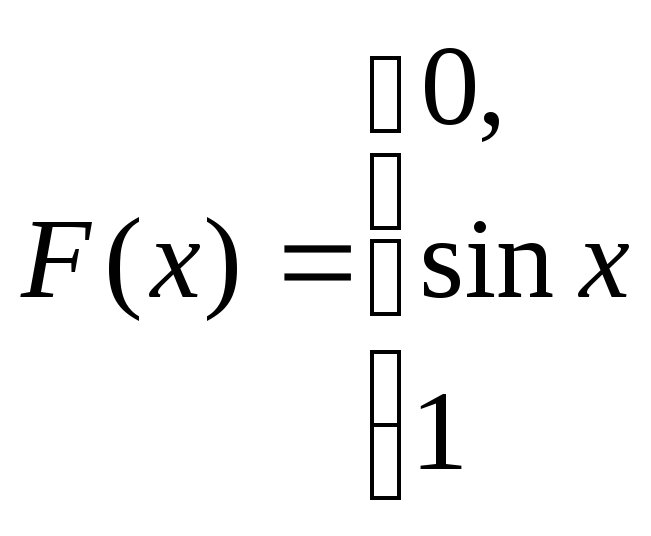 ,
при
,
при 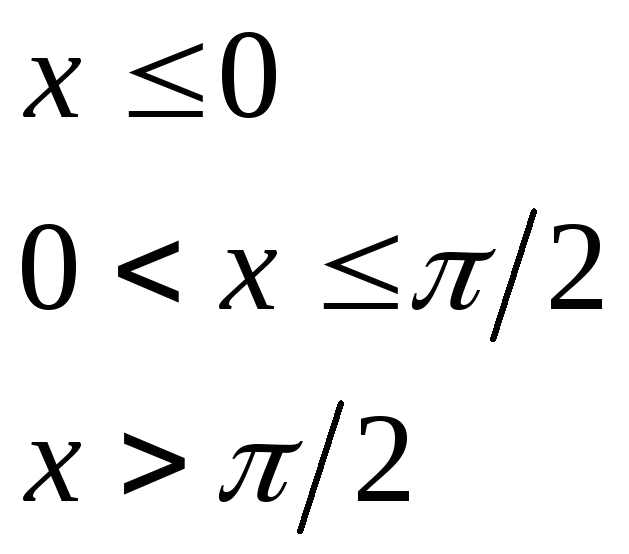
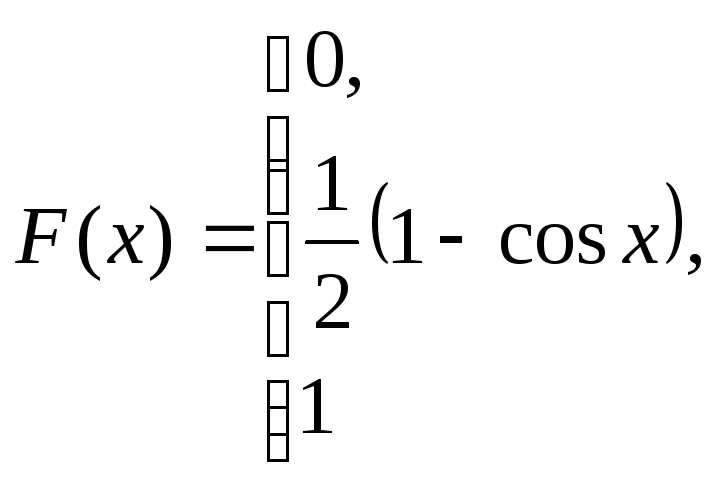 при
при 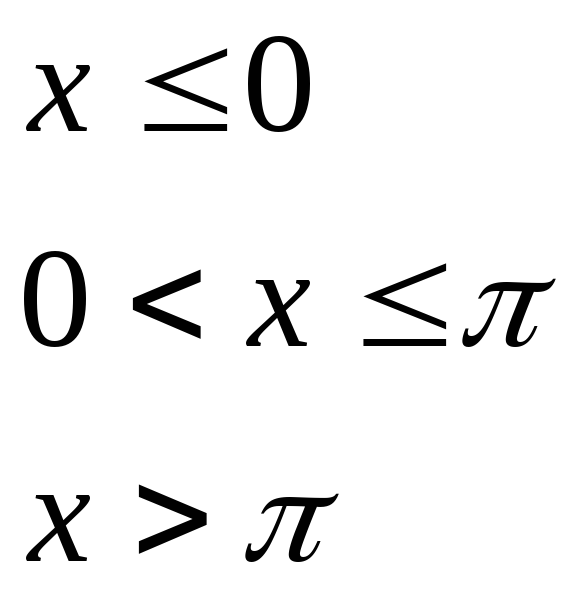
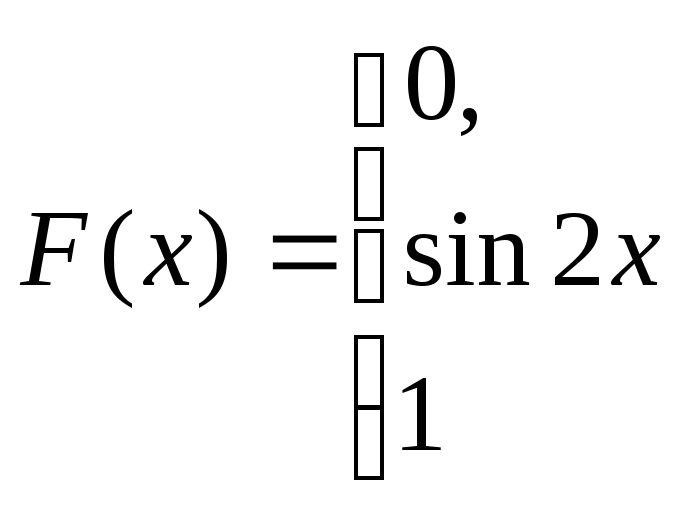 ,
при
,
при 
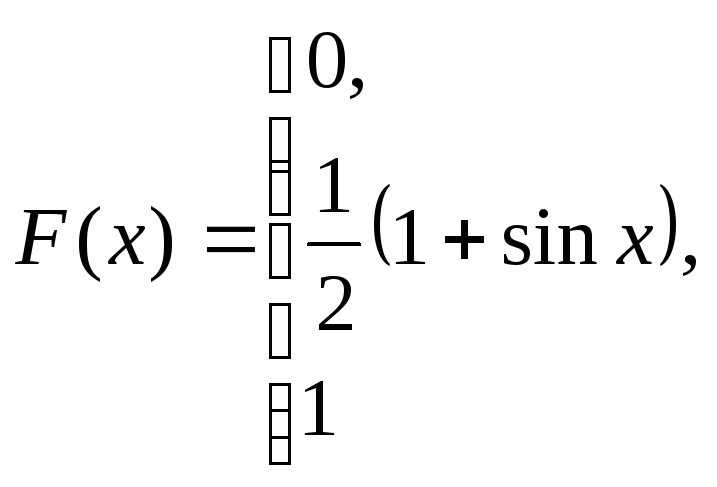 при
при
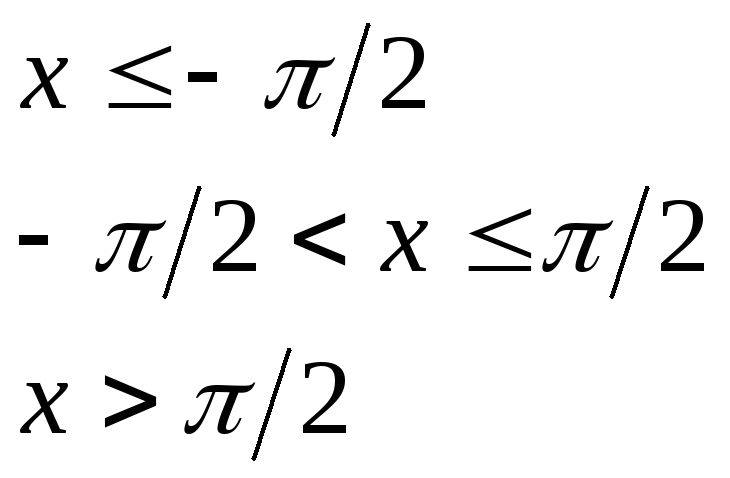
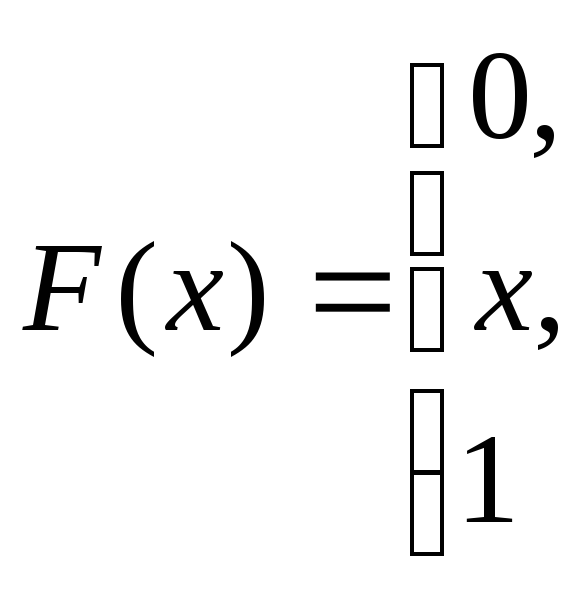 при
при 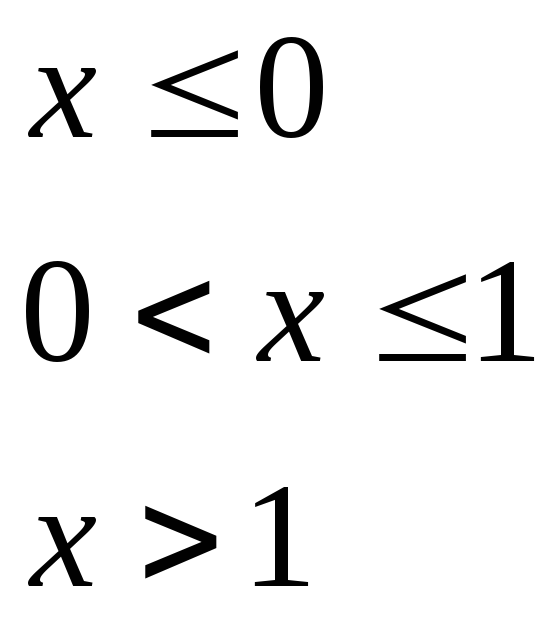
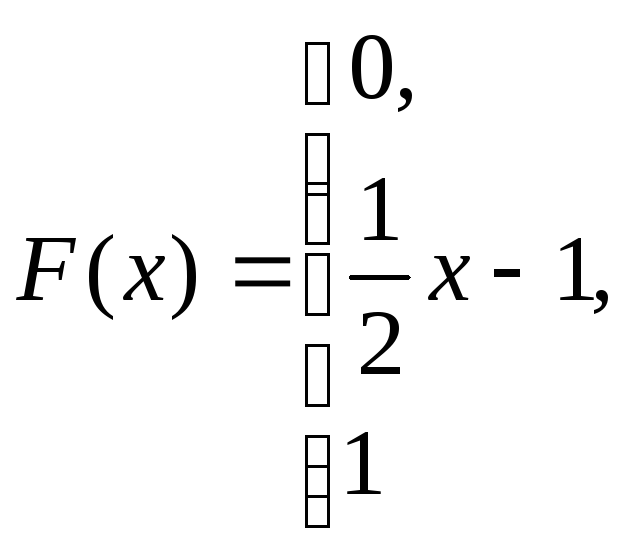 при
при 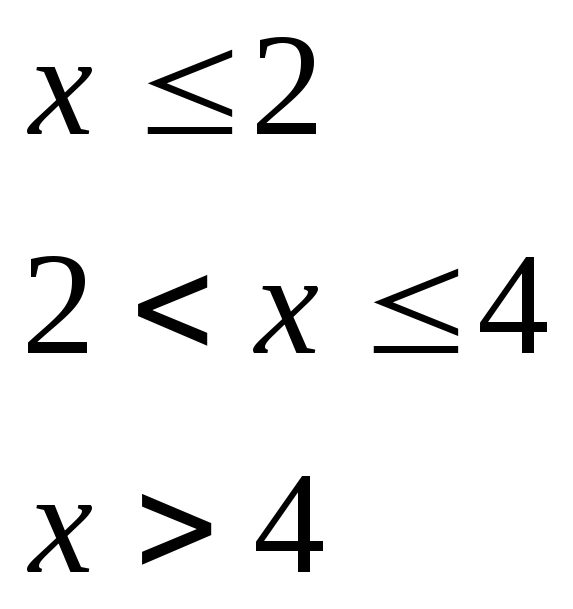
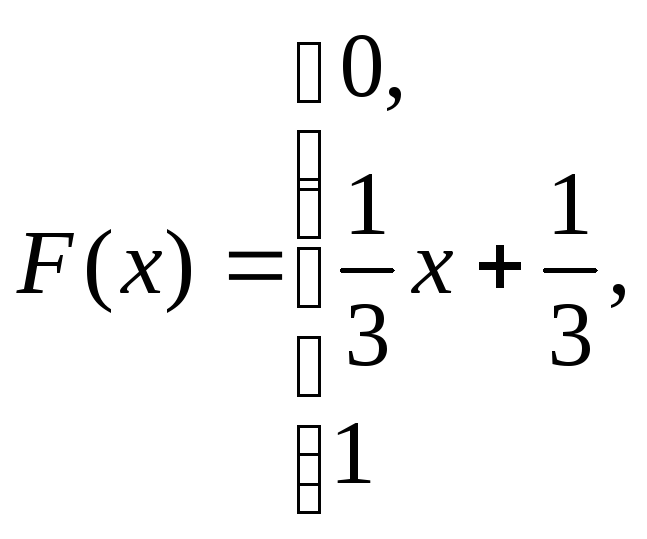 при
при 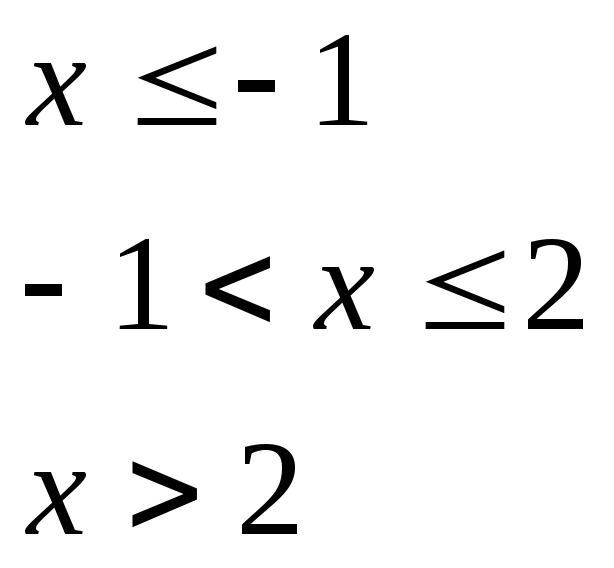
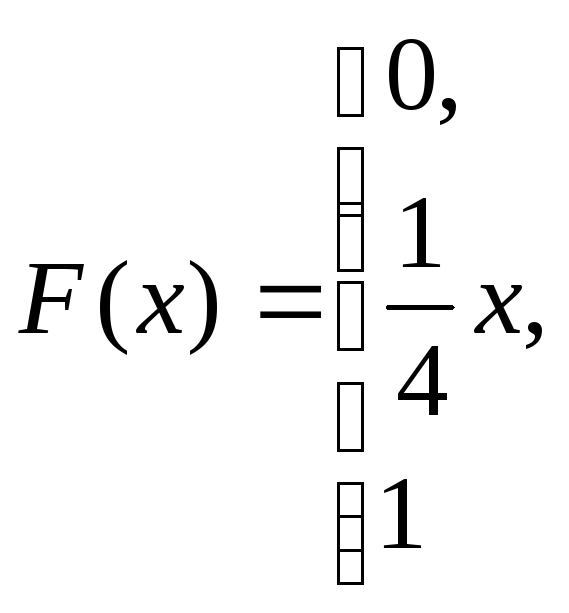 при
при 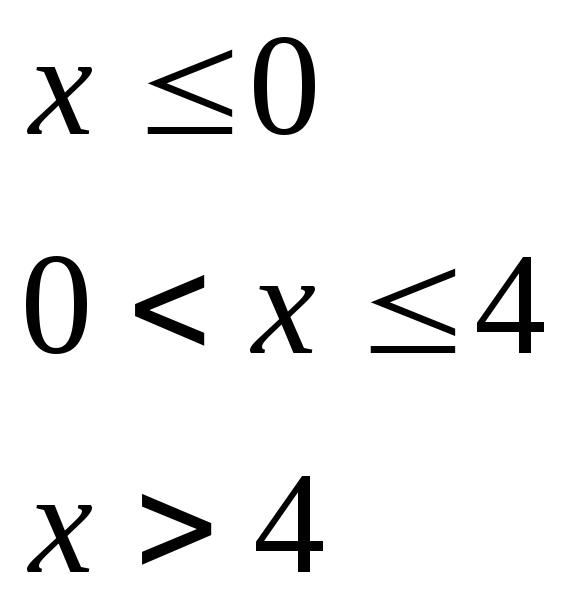
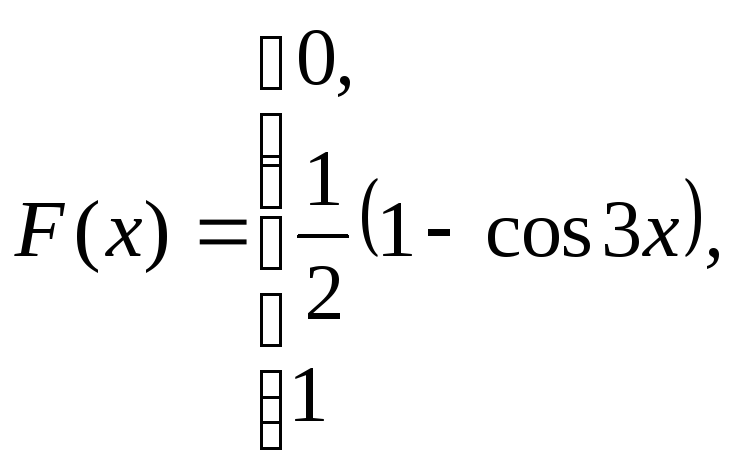 при
при
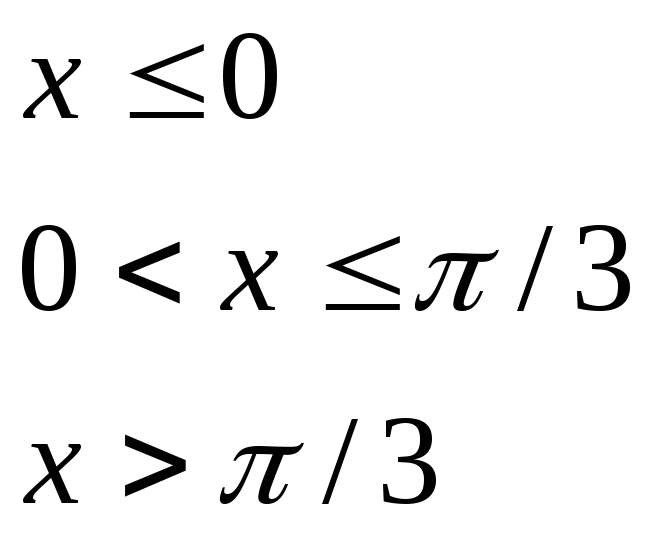
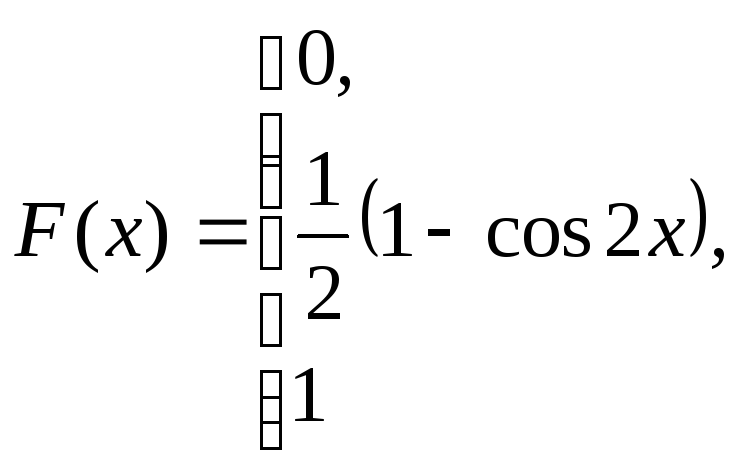 при
при 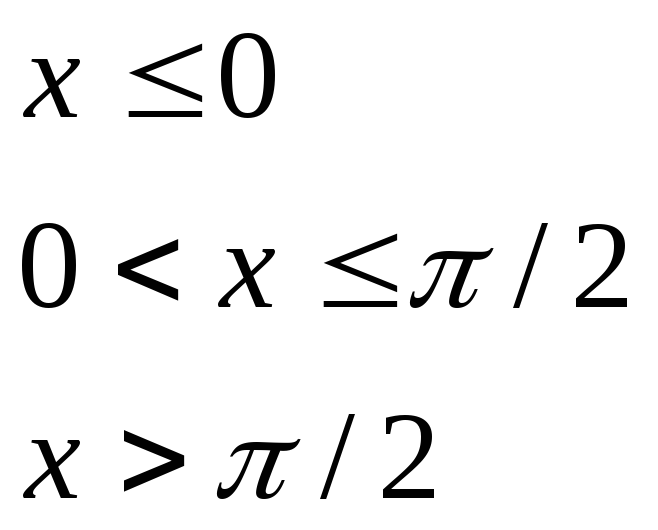
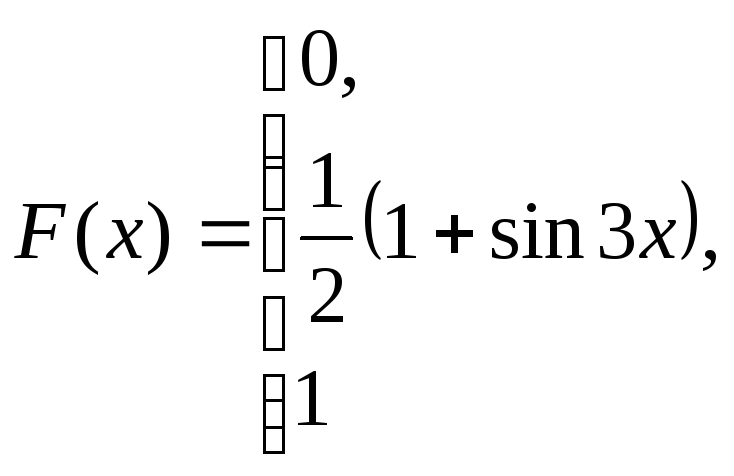 при
при
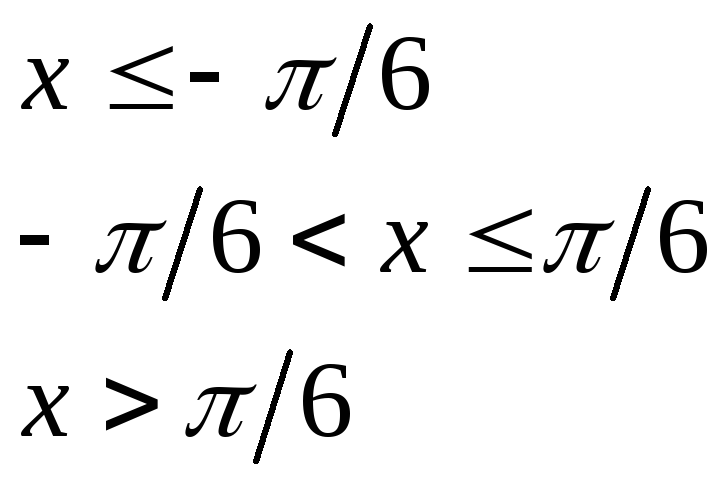
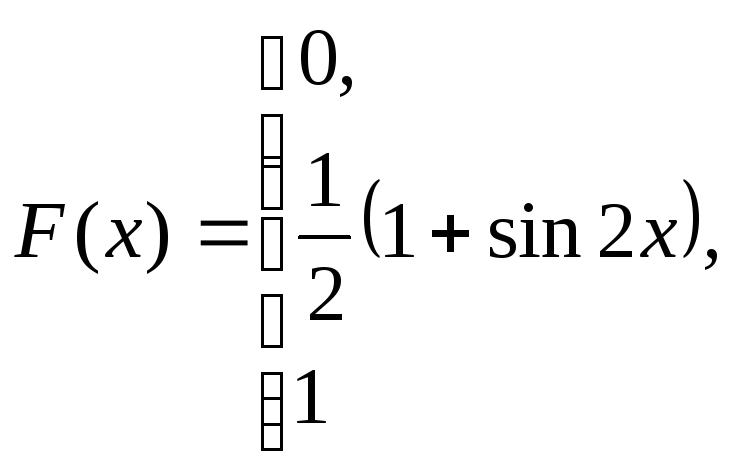 при
при
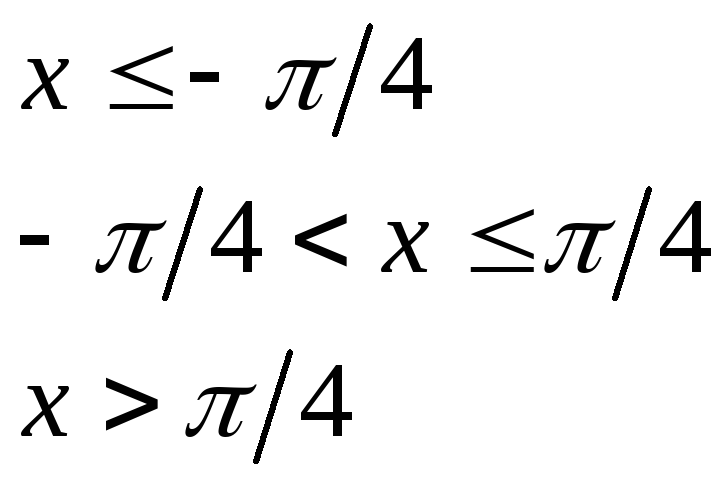
 при
при 
 при
при 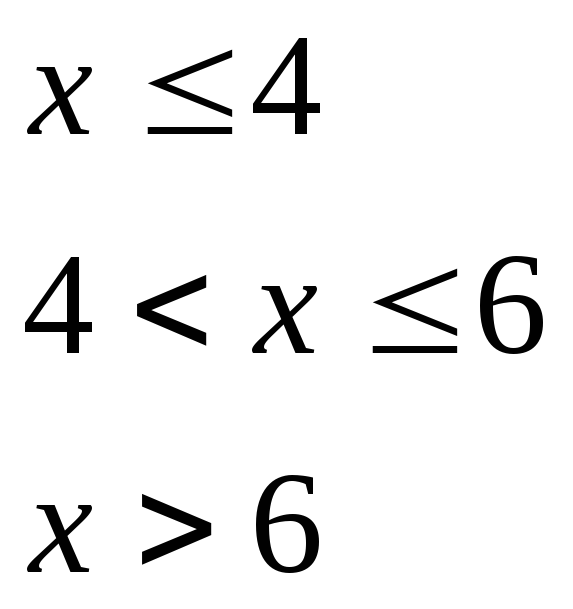
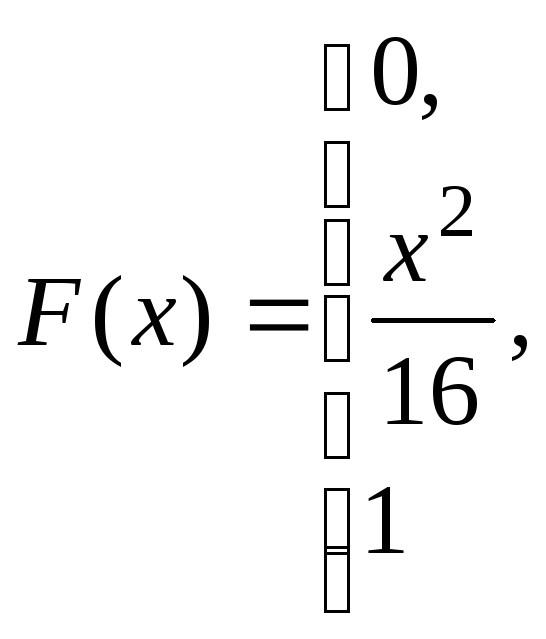 при
при 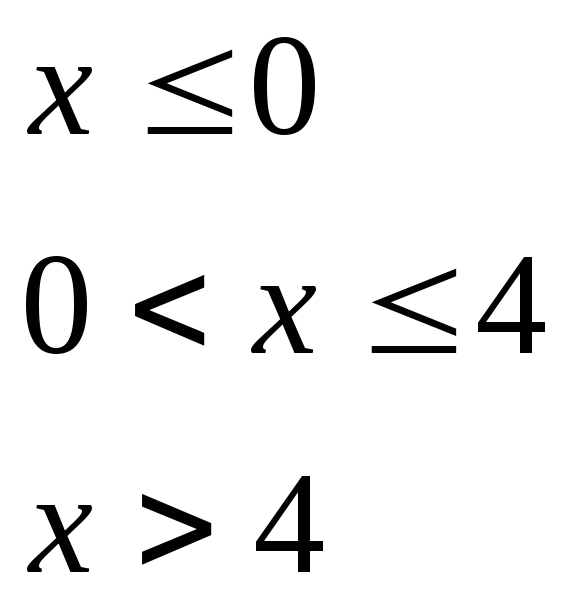
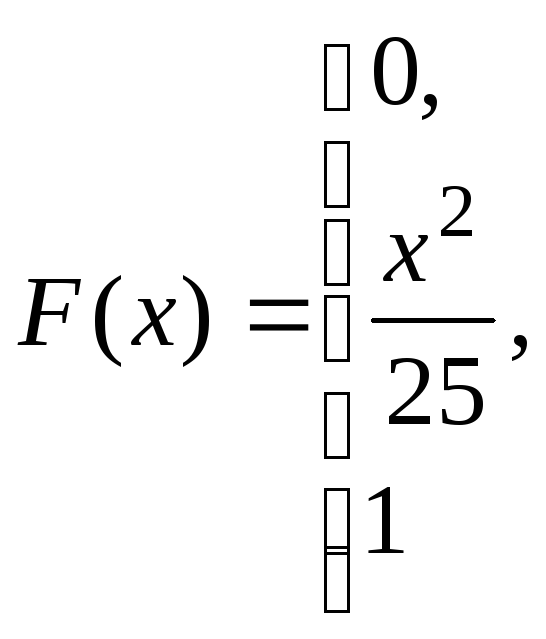 при
при 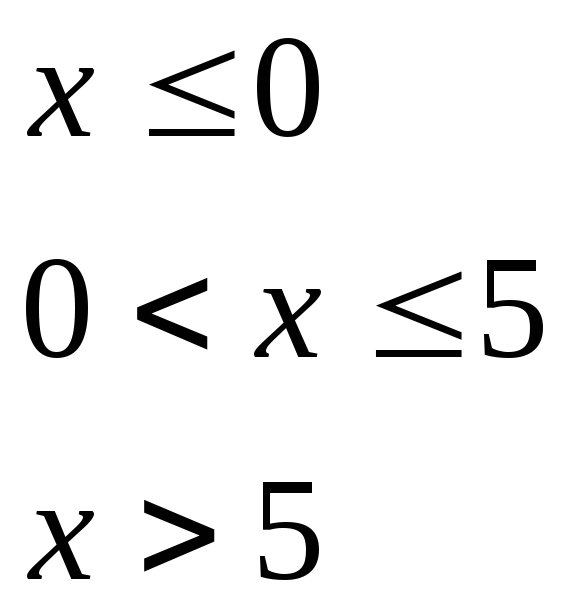
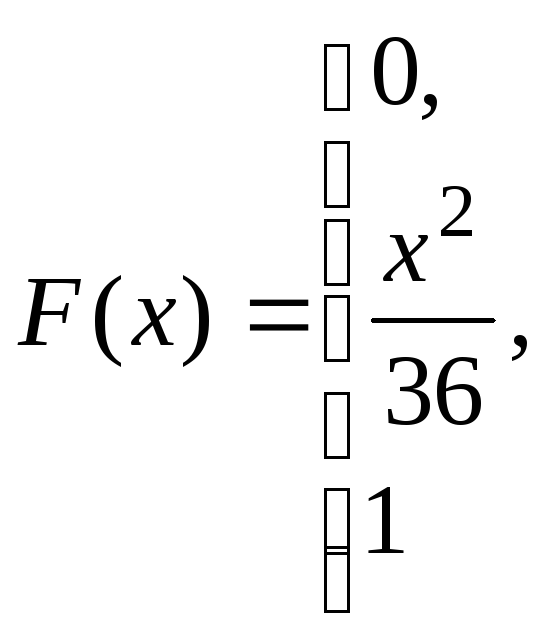 при
при 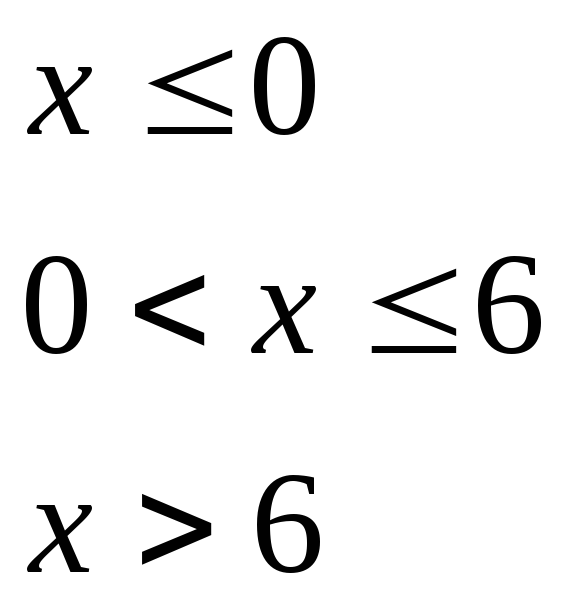
 при
при 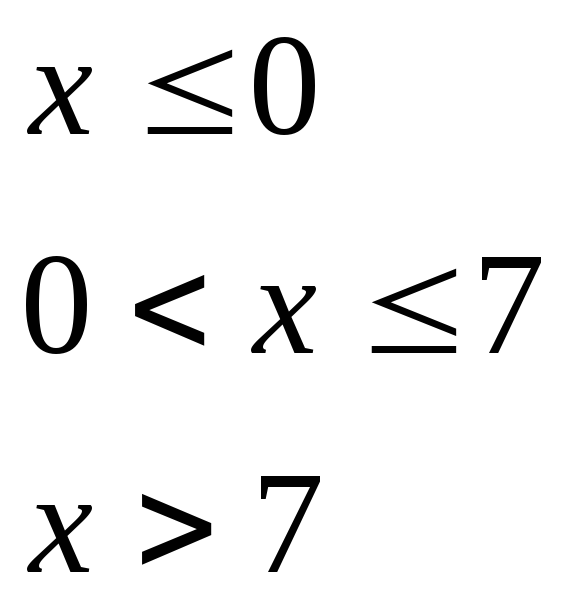
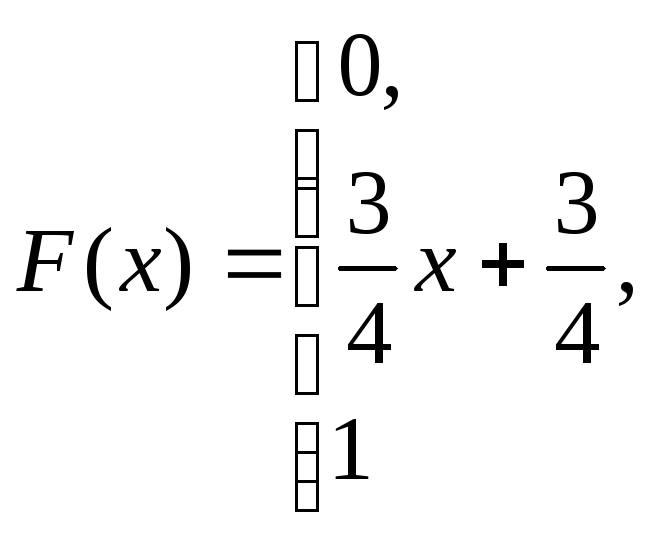 при
при 
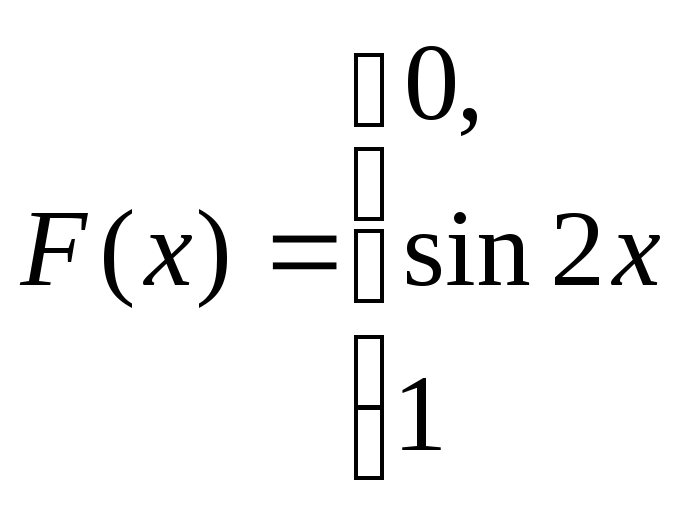 ,
при
,
при 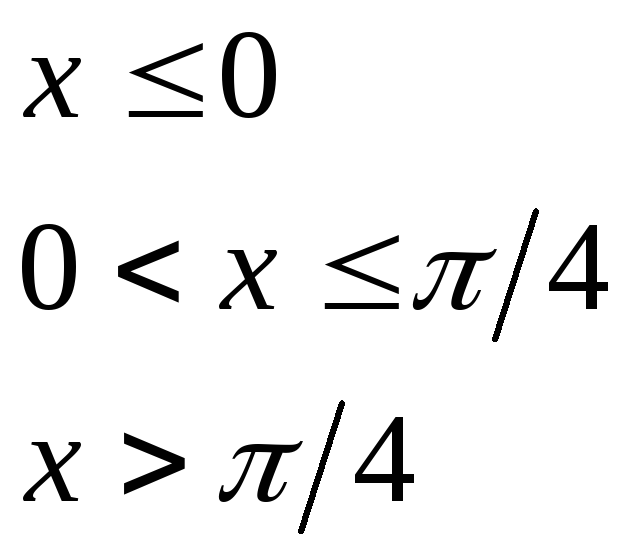
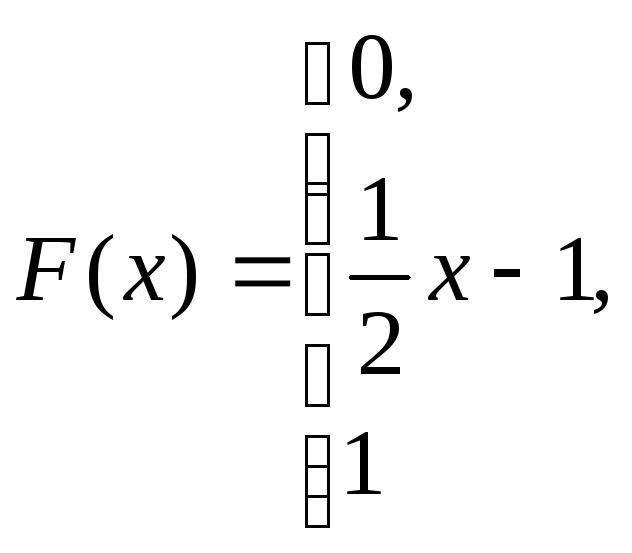 при
при 
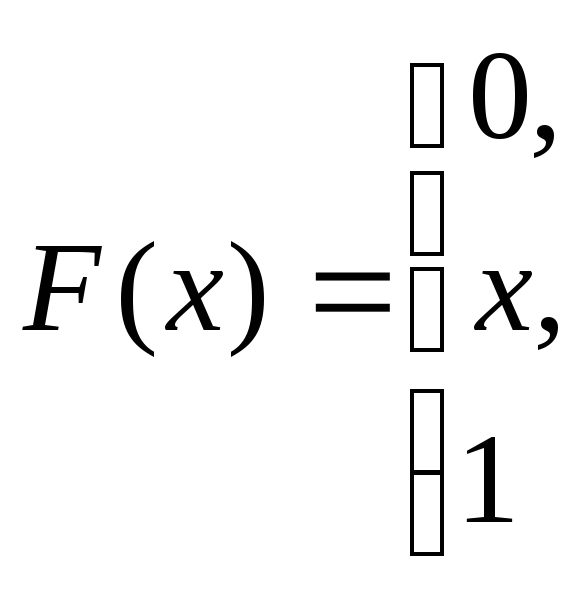 при
при 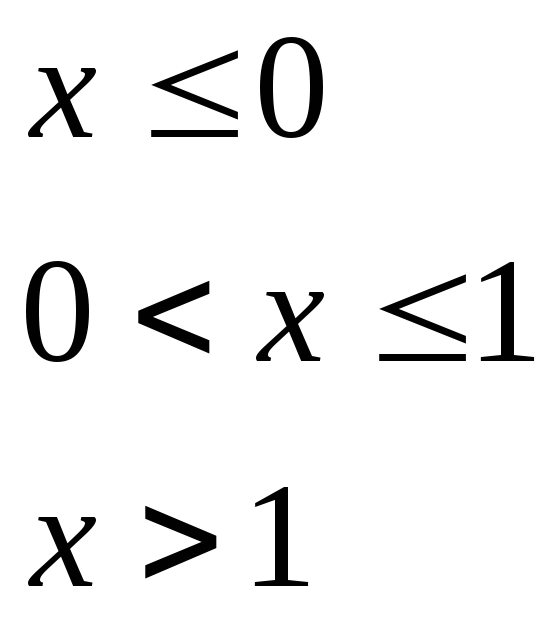
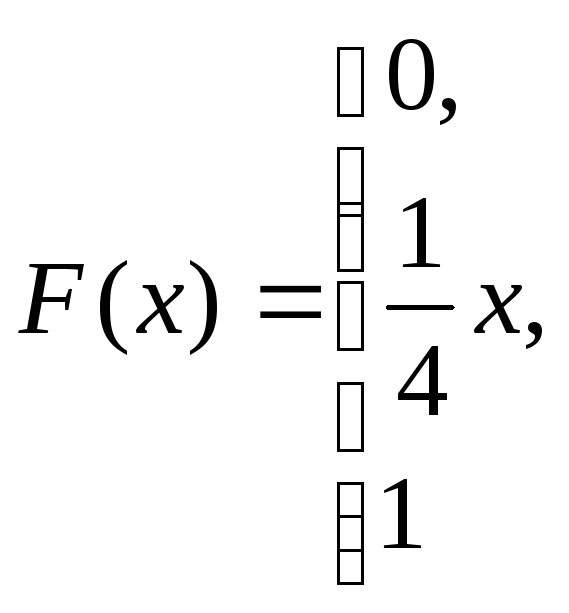 при
при 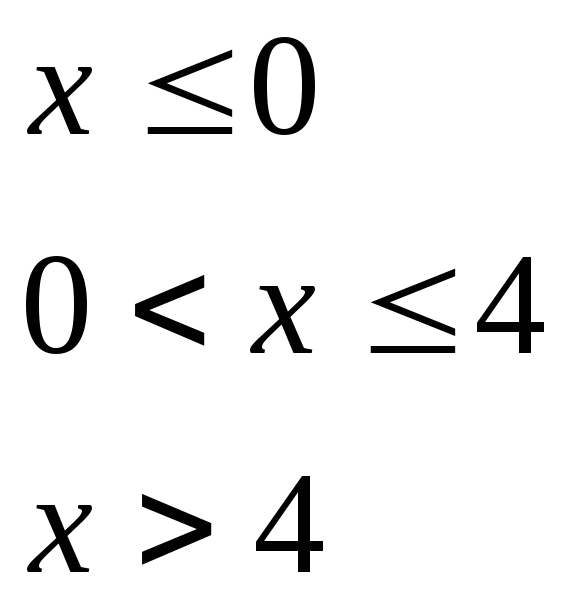
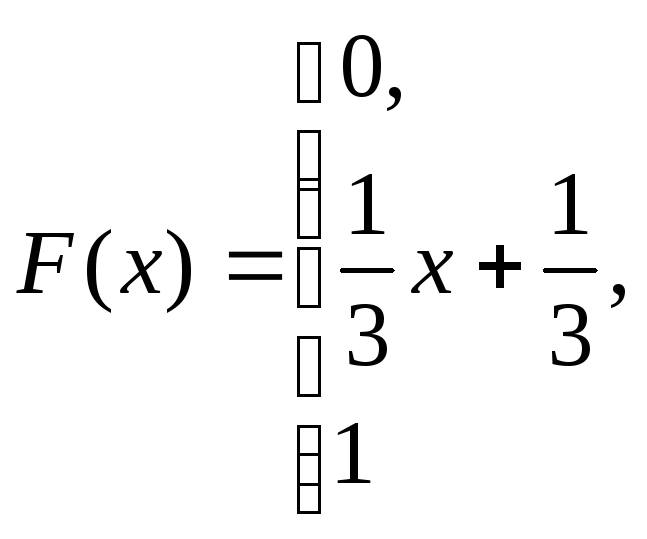 при
при