
- •Міністерство освіти та науки України
- •Передмова
- •Вибір варіанту, рекомендації до виконання і вимоги до оформлення робіт
- •3. Статика Основні поняття
- •Основні типи в'язей. Реакції в'язей
- •Завдання с-1. Рівновага тіла під дією плоскої системи сил
- •Приклад с-1
- •Завдання с-2. Рівновага складеної конструкції під дією плоскої системи сил
- •Завдання с-3. Рівновага тіла під дією просторової системи сил
- •4. Кінематика Основні поняття
- •Завдання к-1. Кінематика точки
- •Приклад к-1
- •Завдання к-2. Кінематика простих рухів тіл
- •Завдання к-3. Дослідження плоского руху твердого тіла
- •Завдання к-4. Складний рух точки
- •5. Література
- •П р и м і т к и
Приклад к-1
Рух
точки відбувається в площині
![]() і заданий параметричними рівняннями:
і заданий параметричними рівняннями:
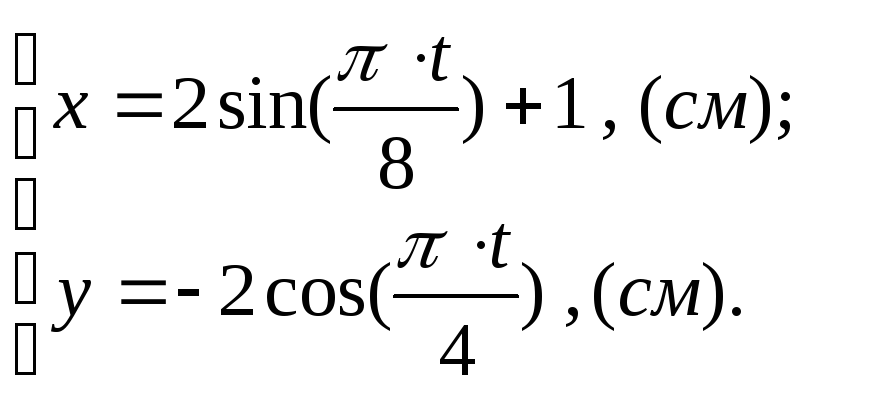 (1)
(1)
Визначити:
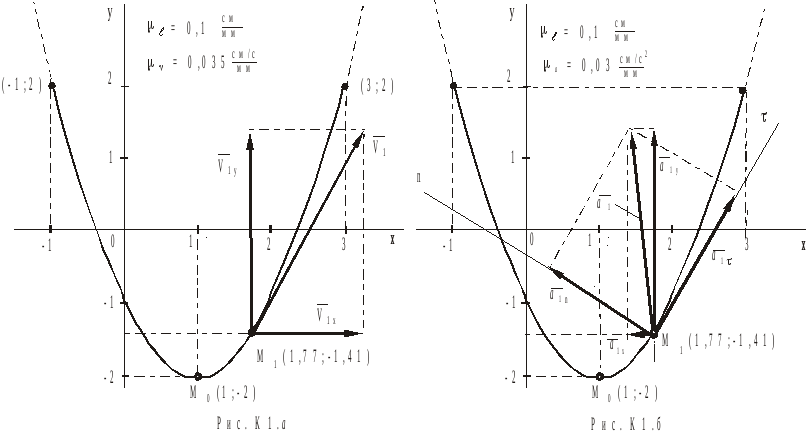
Рівняння траєкторії руху точки. Зобразити траєкторію на рисунку.
Положення точки на траєкторії в момент часу
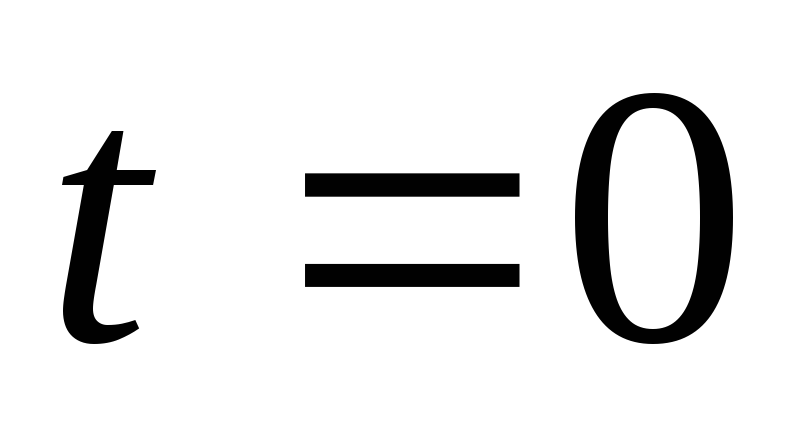 і
і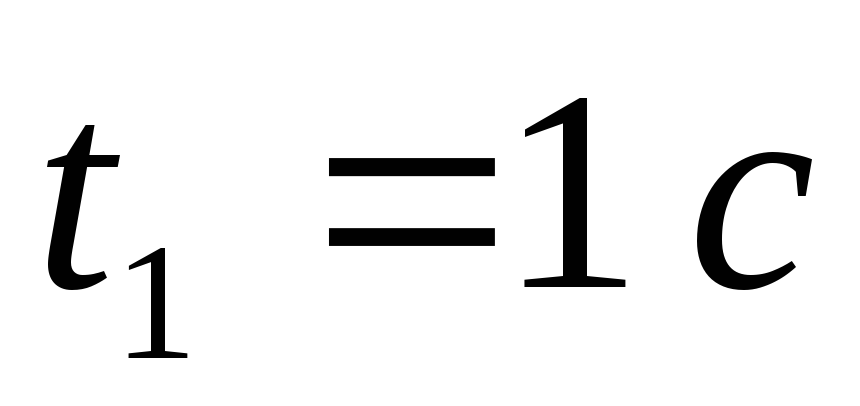 .
.Швидкість точки в момент часу
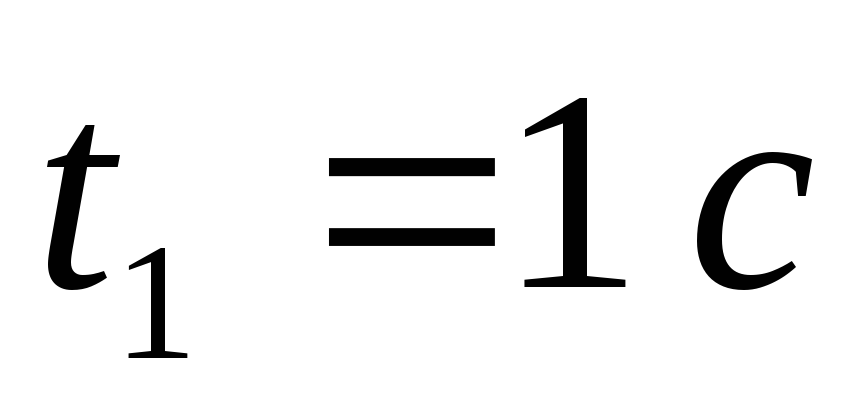 .
.Прискорення точки в момент часу
 .
.Дотичне і нормальне прискорення точки в момент часу
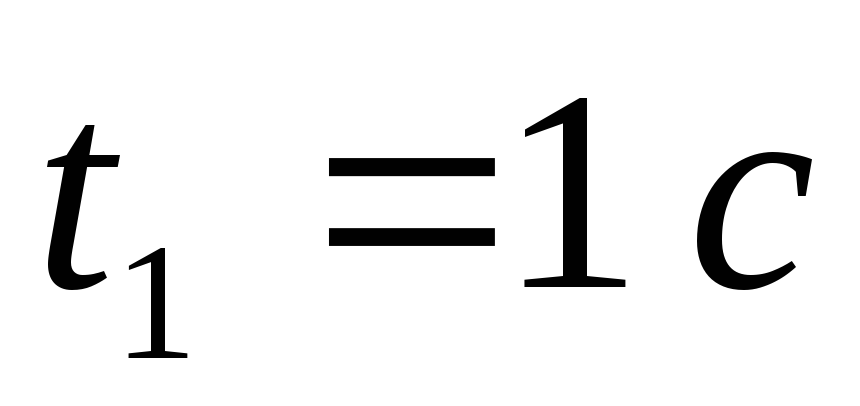 .
.Радіус кривизни траєкторії точки в момент часу
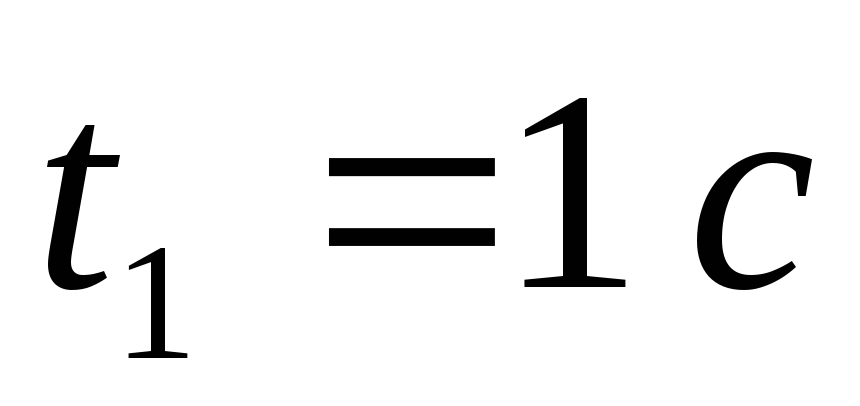 .
.
Усі знайдені величини зобразити на рисунку в масштабі.
Розв’язування.
Для визначення рівняння траєкторії точки виключимо параметр
 із рівнянь руху (1). Ураховуючи, що час
із рівнянь руху (1). Ураховуючи, що час входить в аргумент тригонометричних
функцій, скористаємося формулою:
входить в аргумент тригонометричних
функцій, скористаємося формулою:
![]() , тобто
, тобто
![]() (2)
(2)
З рівнянь руху знаходимо вирази відповідних функцій і підставляємо в рівність (2)
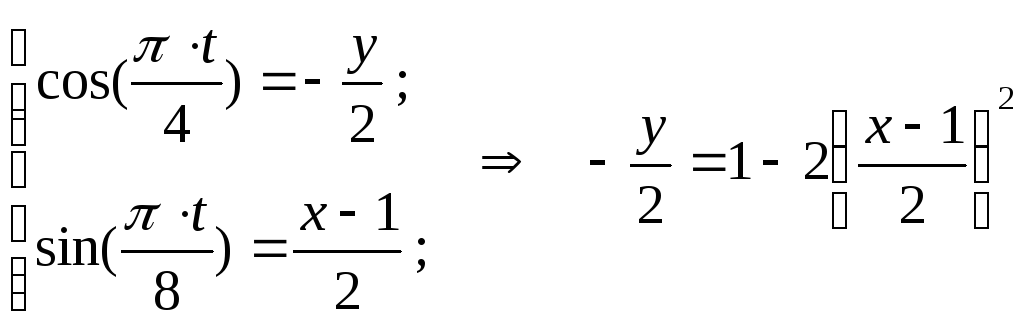 чи
чи
![]() (3)
(3)
Рівняння параболи (3) є рівнянням траєкторії руху точки. Враховуючи , що
-1![]() та -1
та -1![]() ,
маємо обмеження для
,
маємо обмеження для![]() та
та
![]() :
:
-1![]() та -2
та -2![]() , тобто траєкторією руху точки є частина
параболи. Побудуємо траєкторію точки
на рисунку К1.а з масштабним коефіцієнтом
, тобто траєкторією руху точки є частина
параболи. Побудуємо траєкторію точки
на рисунку К1.а з масштабним коефіцієнтом![]() .
.
Визначимо початкове положення точки і положення точки в момент часу
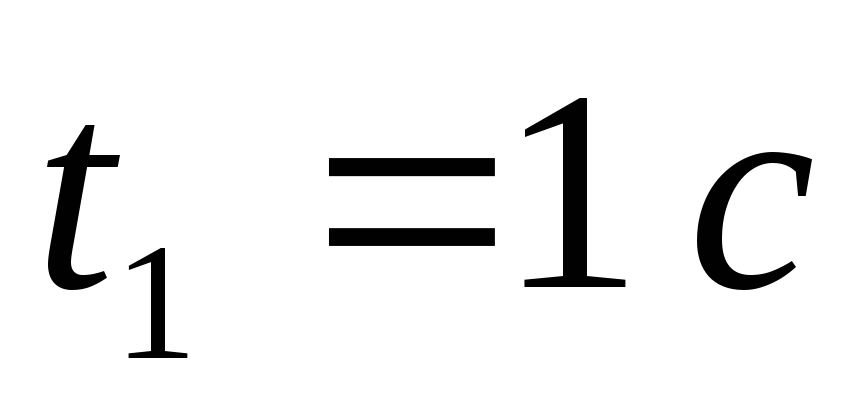 на траєкторії. Для цього підставимо в
рівняння (1) час
на траєкторії. Для цього підставимо в
рівняння (1) час і
і .
Отримаємо:
.
Отримаємо:
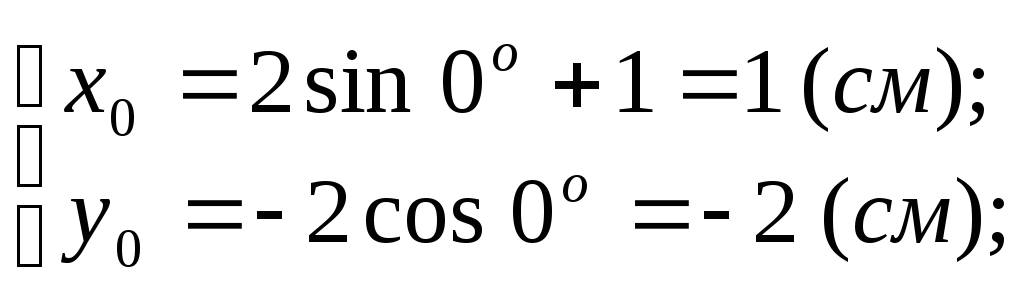 (4)
(4)
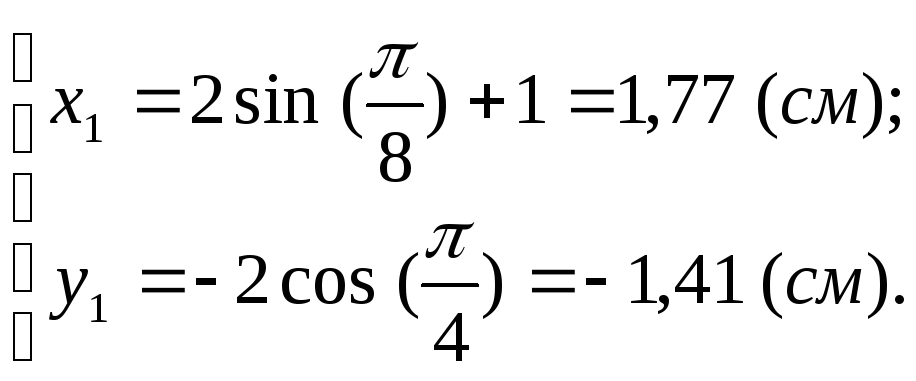 (5)
(5)
Таким
чином
![]() (1;-2) , а
(1;-2) , а![]() (1,77;
-1,41). Покажемо ці точки на траєкторії
(рис.К1.а).
(1,77;
-1,41). Покажемо ці точки на траєкторії
(рис.К1.а).
Визначимо швидкість точки. Проекції швидкості в довільний момент часу дорівнюють:
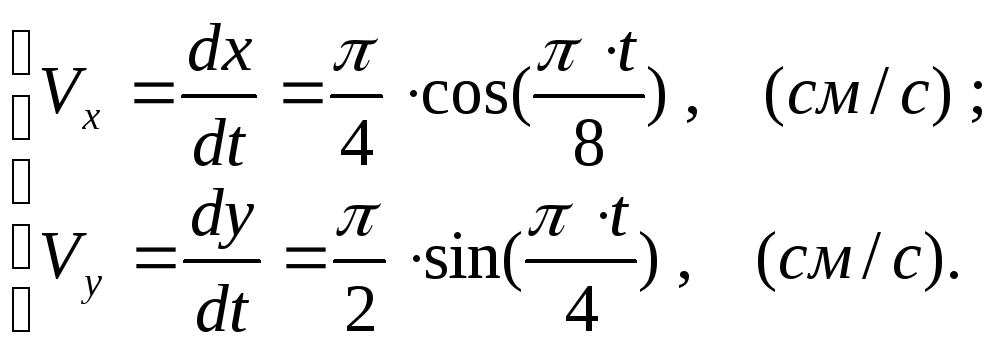 (6)
(6)
В
момент часу
![]()
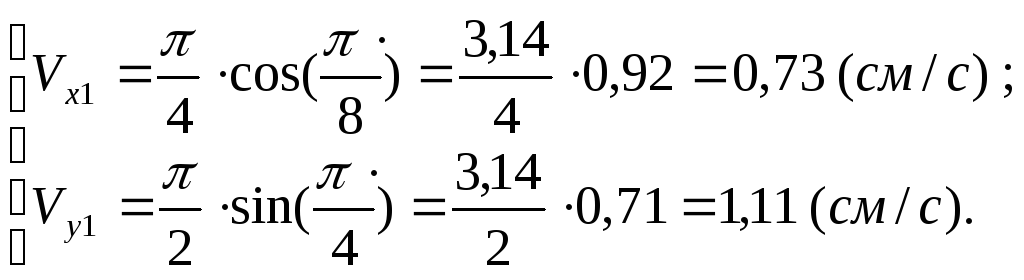
Модуль
швидкості для моменту
![]() :
:
![]() .
.
Побудуємо
вектор швидкості
![]() точки
точки![]() по його складовим
по його складовим
![]() ,
,
![]() ,
де
,
де![]() і
і![]() в масштабі
в масштабі![]() (рис.К1.а).
(рис.К1.а).
Визначимо прискорення точки. Проекції прискорення в довільний момент часу дорівнюють:
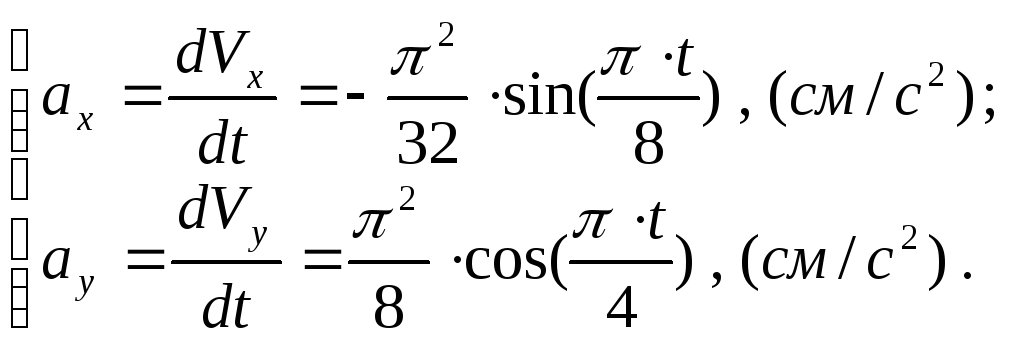 (7)
(7)
У момент
часу
![]() одержимо:
одержимо:
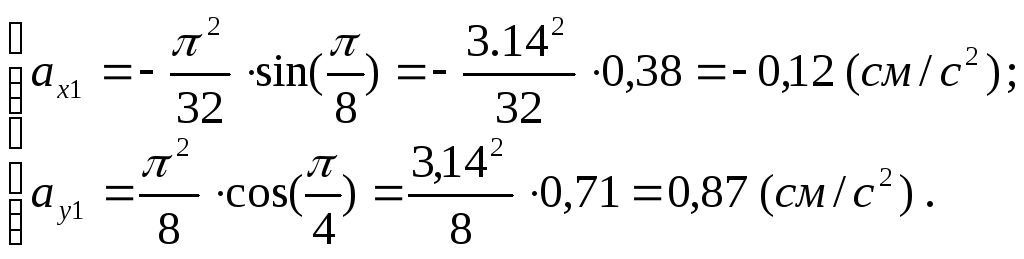
Модуль
прискорення точки
![]() :
:
![]()
Вектор
![]() повного прискорення точки
повного прискорення точки![]() побудуємо по його складових
побудуємо по його складових![]() ,
де
,
де![]() і
і![]() в масштабі
в масштабі![]() (рис.К1.б).
(рис.К1.б).
Визначимо дотичне і нормальне прискорення точки в момент часу
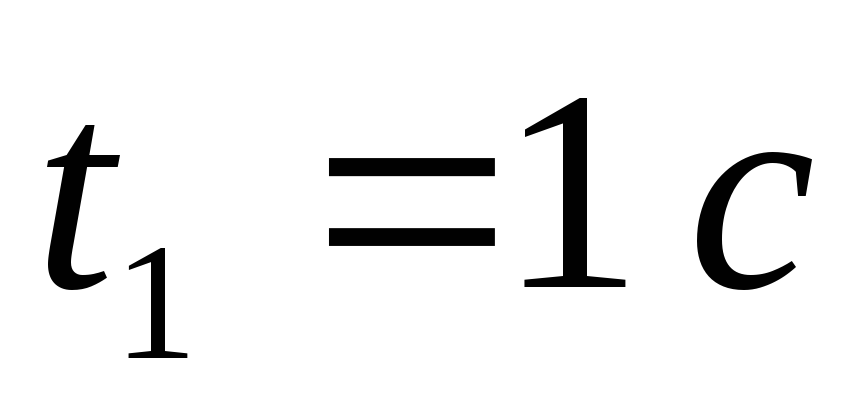 ,
використовуючи формули :
,
використовуючи формули :
Побудуємо
вектор
![]() повного прискорення точки
повного прискорення точки![]() по проекціях
по проекціях![]() і
і![]() (рис.К1.б). Для зображення векторів
використовуємо той же масштаб, тобто
(рис.К1.б). Для зображення векторів
використовуємо той же масштаб, тобто![]() Значення дотичного прискорення
Значення дотичного прискорення![]() виявилося
додатнім, тому відкладаємо його по
осі М
виявилося
додатнім, тому відкладаємо його по
осі М![]() (дотичної до траєкторії) у напрямку
вектора швидкості
(дотичної до траєкторії) у напрямку
вектора швидкості![]() .
Вектор нормального прискорення
.
Вектор нормального прискорення![]() направимо
перпендикулярно до осі М
направимо
перпендикулярно до осі М![]() по нормалі М
по нормалі М![]() (вбік увігнутості траєкторії).
(вбік увігнутості траєкторії).
Збіг
векторів повного прискорення при
вирішенні задачі в нерухомій системі
координат Оxy
і рухомій
системі координат М![]() говорить про правильність результату.
говорить про правильність результату.
6.
Радіус кривизни траєкторії в точці
![]() визначимо по формулі:
визначимо по формулі:
В
Рівняння
траєкторії
Положення
точок
Швидкість
точки при
Прискорення
точки при
Дотичне
та нормальне прискорення
Радіус
кривизни траєкторії при
![]()
![]() (1;-2)
;
(1;-2)
;![]() (1,77;
-1,41).
(1,77;
-1,41).![]()
![]()
![]()
![]()
![]() і
і![]() .
.![]()
![]()
Завдання к-2. Кінематика простих рухів тіл
Умова завдання. Механізм складається зі ступінчастих коліс 1-3, зубчастої рейки 4 і вантажу 5 (рис.К2.0 – К2.9, табл.К2). Колеса пов'язані між собою зубчастою або пасовою передачею; рейка знаходиться у зубчастім зачепленні з одним із коліс; а вантаж прикріплений до нитки, яка намотана на колесо. При русі механізму відносне ковзання його елементів не відбувається, а пас і нитка вважаються нерозтяжними.
Радіуси
зовнішніх та внутрішніх ободів (ступіней)
коліс дорівнюють відповідно: у колеса
1 -
![]() і
і![]() ;
у колеса 2 -
;
у колеса 2 -![]() і
і![]() ;
у колеса 3 -
;
у колеса 3 -![]() і
і![]() .
На ободах коліс розташовані точки
.
На ободах коліс розташовані точки![]() і
і![]() .
.
У стовпці
«Дано» табл.К2 зазначений закон руху
ведучої ланки механізму. Додатний
напрямок для кута
![]() - проти руху годинникової стрілки; для
відстані
- проти руху годинникової стрілки; для
відстані![]() - униз ;
- униз ;![]() -
виражено врад,
-
виражено врад,
![]() - усм,
час
- усм,
час
![]() - усек.
- усек.
Визначити.
В момент часу
![]() визначити указані в стовпцях «Знайти»
швидкості та прискорення відповідних
тіл і точок тіл. Знайдені величини
показати на рисунку.
визначити указані в стовпцях «Знайти»
швидкості та прискорення відповідних
тіл і точок тіл. Знайдені величини
показати на рисунку.
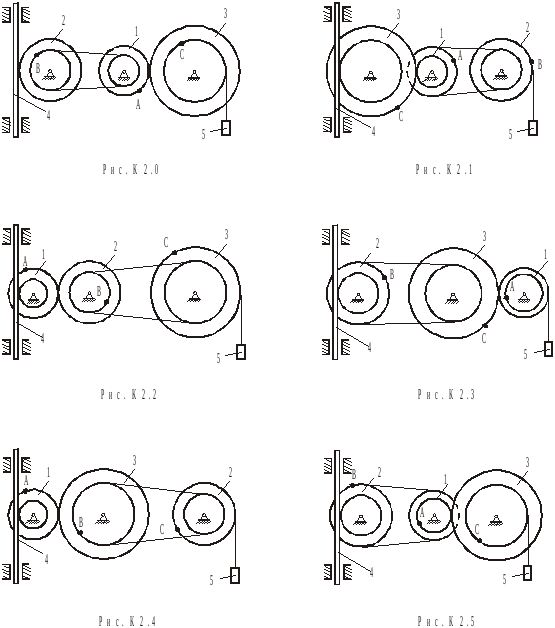
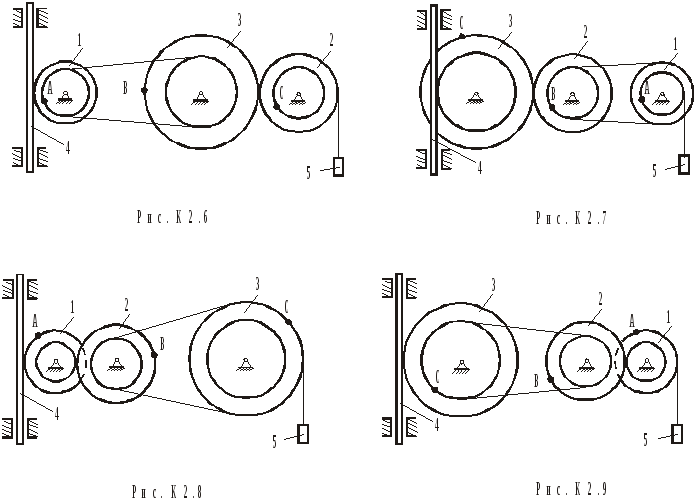
Табл.К2
|
Номер рядка даних |
Дано |
Знайти | |
|
Швидкості |
Прискорення | ||
|
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
Теоретичне обґрунтування : [4] §.48-51, [5] Разд.II, гл. 2,§ 1-3, [6] Разд.2, гл. X ,§ 78-84; [7]; [8].
Методичні вказівки. Задача К-2 – на дослідження простих видів руху твердого тіла (поступального й обертального).
Варто розрізняти кінематичні характеристики твердих тіл і кінематичні характеристики окремих точок цих тіл.
При поступальному русі тіла
Кінематичні характеристики тіла – лінійна швидкість тіла і лінійне прискорення тіла. Кінематичні характеристики точки тіла - швидкість точки і прискорення точки.
Закон
руху тіла задається рівнянням руху
однієї з його точок
![]() .
Швидкість тіла -
.
Швидкість тіла -![]() .
Прискорення тіла -
.
Прискорення тіла -![]() .
.
Кінематичні характеристики тіла й окремих точок тіла збігаються.
При обертальному русі тіла навколо нерухомої осі
Кінематичні характеристики тіла – кутова швидкість тіла і кутове прискорення тіла. Кінематичні характеристики точки тіла – лінійна швидкість точки і лінійне прискорення точки.
Закон
обертального руху тіла задається
залежністю кута повороту від часу:
![]() .
Кутова швидкість -
.
Кутова швидкість -![]() .
Якщо алгебраїчне значення
.
Якщо алгебраїчне значення![]() ,то
напрям
,то
напрям![]() і
і![]() збігається; якщо
збігається; якщо![]() ,
то вони спрямовані протилежно. Кутове
прискорення -
,
то вони спрямовані протилежно. Кутове
прискорення -![]() . Якщо
. Якщо![]() і
і![]() мають однакові знаки , то рух прискорений,
якщо різні – сповільнений.
мають однакові знаки , то рух прискорений,
якщо різні – сповільнений.
Швидкість
довільної точки
![]() тіла, якщо тіло обертається навколо
нерухомої осі, визначається за формулою
тіла, якщо тіло обертається навколо
нерухомої осі, визначається за формулою![]() ,
де
,
де![]() -
відстань від точки
-
відстань від точки![]() до
осі обертання. Вектор
до
осі обертання. Вектор![]() швидкості точки
швидкості точки![]() лежить у площині, перпендикулярній осі
обертання і спрямований по дотичній до
траєкторії руху точки, тобто
лежить у площині, перпендикулярній осі
обертання і спрямований по дотичній до
траєкторії руху точки, тобто![]() ,
за напрямком кутової швидкості.
,
за напрямком кутової швидкості.
Вектор
![]() прискорення довільної точки
прискорення довільної точки![]() тіла, якщо тіло обертається навколо
нерухомої осі, дорівнює геометричній
сумі обертального
тіла, якщо тіло обертається навколо
нерухомої осі, дорівнює геометричній
сумі обертального![]() (дотичного) і доцентрового
(дотичного) і доцентрового![]() (нормального) прискорень, тобто
(нормального) прискорень, тобто![]() ,
де
,
де![]() і
і![]() .
Вектор
.
Вектор![]()
![]() ,
збігається за напрямком зі швидкістю,
якщо рух прискорений, або спрямований
протилежно, якщо рух сповільнений.
Вектор
,
збігається за напрямком зі швидкістю,
якщо рух прискорений, або спрямований
протилежно, якщо рух сповільнений.
Вектор![]() лежить у площині, перпендикулярній осі
обертання і завжди спрямований до осі
обертання.
лежить у площині, перпендикулярній осі
обертання і завжди спрямований до осі
обертання.
Модуль
прискорення точки визначається за
формулою
![]() .
.
Приклад К-2
Механізм складається зі ступінчастих коліс 1-3, зубчастої рейки 4 і вантажу 5 (рис.К2.а). Колеса 1 і 2 пов'язані між собою пасовою передачею; колеса 2 і 3 – зубчастою передачею; рейка 4 знаходиться в зубчастім зачепленні із колесом 1; а вантаж 5 прикріплений до нитки, яка намотана на колесо 3. Пас і нитка нерозтяжні. При русі механізму відносне ковзання елементів не відбувається.
Радіуси
зовнішніх та внутрішніх ободів (ступіней)
коліс дорівнюють відповідно: у колеса
1 -
![]() і
і![]() ;
у колеса 2 -
;
у колеса 2 -![]() і
і![]() ;
у колеса 3 -
;
у колеса 3 -![]() і
і![]() .
.
Р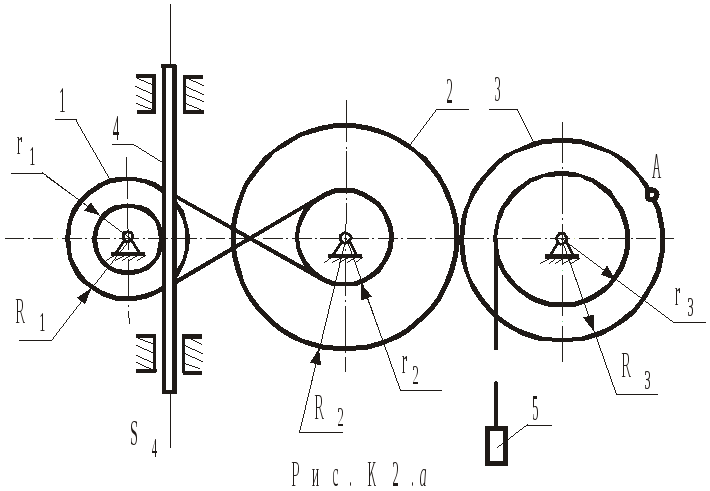 ейка
рухається за законом
ейка
рухається за законом![]() . Вісь
. Вісь![]() спрямована вертикально вниз. Точка
спрямована вертикально вниз. Точка![]() належить зовнішньому ободу колеса 3.
належить зовнішньому ободу колеса 3.
Визначити
швидкості та прискорення всіх тіл і
точки
![]() в момент часу
в момент часу![]() .
Усі знайдені величини зобразити на
рисунку.
.
Усі знайдені величини зобразити на
рисунку.
Розв’язування.
Механізм (рис.К2.а) є механічною системою з одним ступенем вільності. Тобто рух кожного з елементів пов’язаний з рухом інших елементів жорсткими кінематичними співвідношеннями. Тому, якщо рух одного з тіл задається, кінематичні характеристики інших тіл і їх точок фактично є визначеними. В умові даної задачі задається рух рейки 4.
Визначимо швидкості тіл механізму.
Знаючи закон поступального руху рейки 4, знайдемо її швидкість
![]() . При
. При
![]()
![]() .
.
Знак «
- » указує на те, що в даний момент часу
вектор швидкості
![]() спрямований
протилежно додатному напрямку осі
спрямований
протилежно додатному напрямку осі![]() ,
тобто вгору (рис.К2.б).
,
тобто вгору (рис.К2.б).
Рейка 4 контактує без ковзання з внутрішнім ободом колеса 1. Враховуючи це, отримаємо рівняння зв’язку рухів тіл 1 і 4:
![]()
![]()
![]() .
При
.
При
![]() одержимо
одержимо![]() .
.
Напрямок
кутової швидкості
![]() залежить від напрямку швидкості рейки.
У даному випадку
залежить від напрямку швидкості рейки.
У даному випадку![]() спрямована проти руху годинникової
стрілки.
спрямована проти руху годинникової
стрілки.
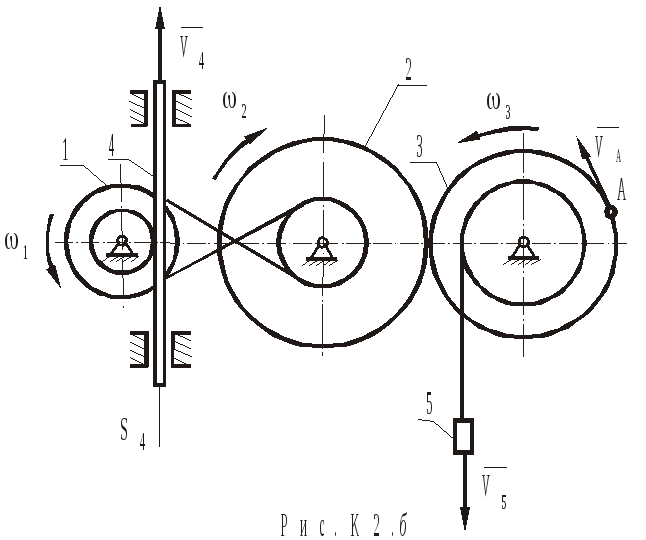
Колеса
1 і 2 з'єднуються зворотною пасовою передачею по зовнішньому
ободу колеса 1 (радіус
![]() )
і внутрішньомуободу
колеса 2 (радіус
)
і внутрішньомуободу
колеса 2 (радіус
![]() )
.
)
.
Швидкість точок паса і швидкість точок коліс по зазначених радіусах однакова і дорівнює:
![]() .
Звідси маємо
.
Звідси маємо
![]() .
.
При
зворотній (перехресної) пасовій передачі
напрямок обертання коліс 1 і 2 протилежний.
Тому кутова швидкість
![]() спрямована
за рухом годинникової стрілки.
спрямована
за рухом годинникової стрілки.
Колеса
2 і 3 зв'язані між собою зубчастим
зачепленням по зовнішніх радіусах
коліс. Тому спільна для обох коліс точка
контакту має швидкість:![]()
![]() .
Звідси маємо
.
Звідси маємо
![]() .
.
При зовнішнім зачепленні напрямок обертання коліс протилежний, тобто колесо 3 обертається проти руху годинникової стрілки.
Вантаж 5 зв'язаний з колесом 3 за допомогою нерозтяжної нитки, намотаної на внутрішній обід колеса. У цьому випадку спільною точкою зв’язку рухів тіл 5 і 3 є точка дотику колеса й нитки, яка має таку ж швидкість як вантаж, тобто:
![]() . У
момент часу
. У
момент часу
![]() маємо
маємо![]() .
.
Напрямок
руху вантажу визначається напрямком
обертання колеса 3, тобто вантаж має
швидкість
![]() , спрямовану вниз.
, спрямовану вниз.
Визначимо швидкість точки
 колеса 3 в момент часу
колеса 3 в момент часу .
.
Точка
![]() належить колесу 3, яке обертається з
кутовою швидкістю
належить колесу 3, яке обертається з
кутовою швидкістю![]() і розташована на відстані
і розташована на відстані![]() від осі його обертання. Тому її швидкість
:
від осі його обертання. Тому її швидкість
:
![]() . При
. При
![]() одержимо
одержимо![]() .
.
Вектор
![]() спрямований по дотичній до обода вбік
обертання колеса 3 (рис.К2.б).
спрямований по дотичній до обода вбік
обертання колеса 3 (рис.К2.б).
Визначимо прискорення тіл.
Знаючи закон руху рейки, визначимо її прискорення:
![]() і при
і при
![]()
![]() .
.
М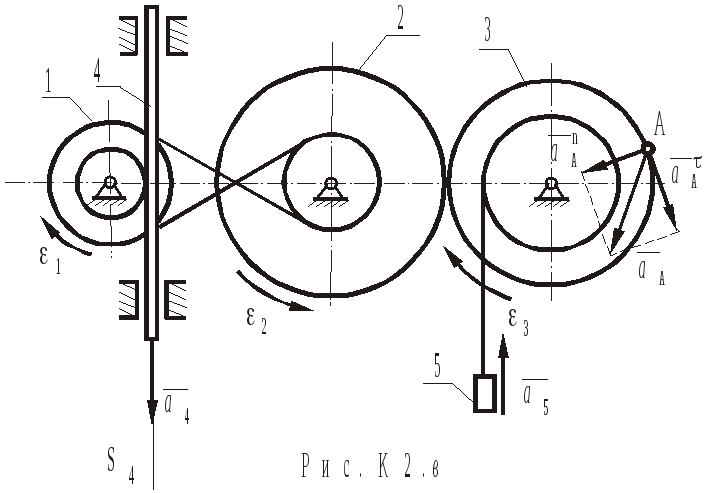 аємо
аємо![]() >
0, тому вектор
>
0, тому вектор![]() спрямований у напрямку осі
спрямований у напрямку осі![]() ,
тобто вниз (рис.К2.в).
,
тобто вниз (рис.К2.в).
Кутове
прискорення колеса 1 залежить від
дотичного прискорення точки з'єднання
з рейкою, що збігається з прискоренням
![]() .
.
Таким чином маємо:
![]()
![]()
![]() .
При
.
При
![]()
![]()
Якщо
вектор
![]() спрямований вниз, то напрямок
спрямований вниз, то напрямок![]() - за рухом годинникової стрілки.
- за рухом годинникової стрілки.
Точки
з'єднання коліс 1 і 2 мають однакові
дотичні прискорення. Тому справедливо:
![]() .
.
Тоді
при
![]()
![]() .
.
Кутове
прискорення
![]() спрямоване протилежно пришвидшенню
спрямоване протилежно пришвидшенню![]() , тобто проти руху годинникової стрілки.
, тобто проти руху годинникової стрілки.
За
аналогією можна записати
![]() ,
тобто при
,
тобто при![]() маємо
маємо
![]() . Напрямок
прискорення
. Напрямок
прискорення
![]() протилежний, тобто за рухом годинникової
стрілки.
протилежний, тобто за рухом годинникової
стрілки.
Прискорення вантажу 5 :
![]() Вектор
Вектор
![]() спрямований
вгору.
спрямований
вгору.
4.
Визначення прискорення
точки
![]() .
.
Точка
![]() належить
колесу 3, яке обертається з кутовою
швидкістю
належить
колесу 3, яке обертається з кутовою
швидкістю![]() і
з кутовим прискоренням
і
з кутовим прискоренням![]() .
Відстань точки
.
Відстань точки![]() від
осі обертання -
від
осі обертання -![]() .
.
Модуль
прискорення точки
![]() визначимо за формулою:
визначимо за формулою:
![]()
Дотичне
прискорення точки
![]() :
:
![]()
Вектор
![]() прикладений у точці
прикладений у точці![]() і спрямований по дотичній до обода
колеса 3 у напрямку кутового прискорення
і спрямований по дотичній до обода
колеса 3 у напрямку кутового прискорення![]() .
.
Нормальне
прискорення точки
![]() :
:
![]()
Вектор
![]() прикладений у точці
прикладений у точці![]() і
спрямований до осі обертання колеса 3.
і
спрямований до осі обертання колеса 3.
Таким
чином :
![]() .
.
Напрямок
повного прискорення точки
![]() визначається векторною сумою векторів
визначається векторною сумою векторів![]() і
і![]() (рис.К2.в).
(рис.К2.в).
Кінематичні
характеристики тіл 1-5 і точки
Колесо
1 -
Колесо
2 -
Колесо
3 -
Рейка
4 -
Вантаж
5 -
Точка
Напрямок
векторів швидкостей і прискорень –
рис.К2,б,в.
![]() :
:
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() -
-![]()
![]()
Відповідь.
